2022年湘教版七年级数学下册2.2.3 运用乘法公式进行计算 同步练习题(含答案)
文档属性
| 名称 | 2022年湘教版七年级数学下册2.2.3 运用乘法公式进行计算 同步练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 75.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览

文档简介
2.2.3 运用乘法公式进行计算
一、选择题
1.下列计算正确的是( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2
C.(x+1)(x-1)=x2-1 D.(x-1)2=x2-1
2.如果(a+b)2-(a-b)2=4,则a和b的关系是( )
A.互为相反数 B.相等 C.互为倒数 D.互为负倒数
3.若a2-b2=-20,a-b=4,则a+b的值是( )
A.-4 B.5 C.-5 D.以上都不对
4.对于任意整数n,多项式(n+7)2-n2都能被( )
A.2整除 B.7整除 C.n整除 D.(n+7)整除
5.下列各式计算正确的是( )
A.(a+b)2=a2+b2 B.a·a2=a3 C.a8·a2=a16 D.a2+a3=a5
6.若实数x、y、z满足(x-z)2-4(x-y)(y-z)=0,则下列式子一定成立的是( )
A.x+y+z=0 B.x+y-2z=0 C.y+z-2x=0 D.z+x-2y=0
7. 设正方形的面积为S1cm2,长方形的面积为S2cm2,如果长方形的长比正方形的边长多3cm,宽比正方形的边长少3cm,则S1与S2的大小关系是( )
A.S1>S2 B.S1<S2 C.S1=S2 D.不能确定
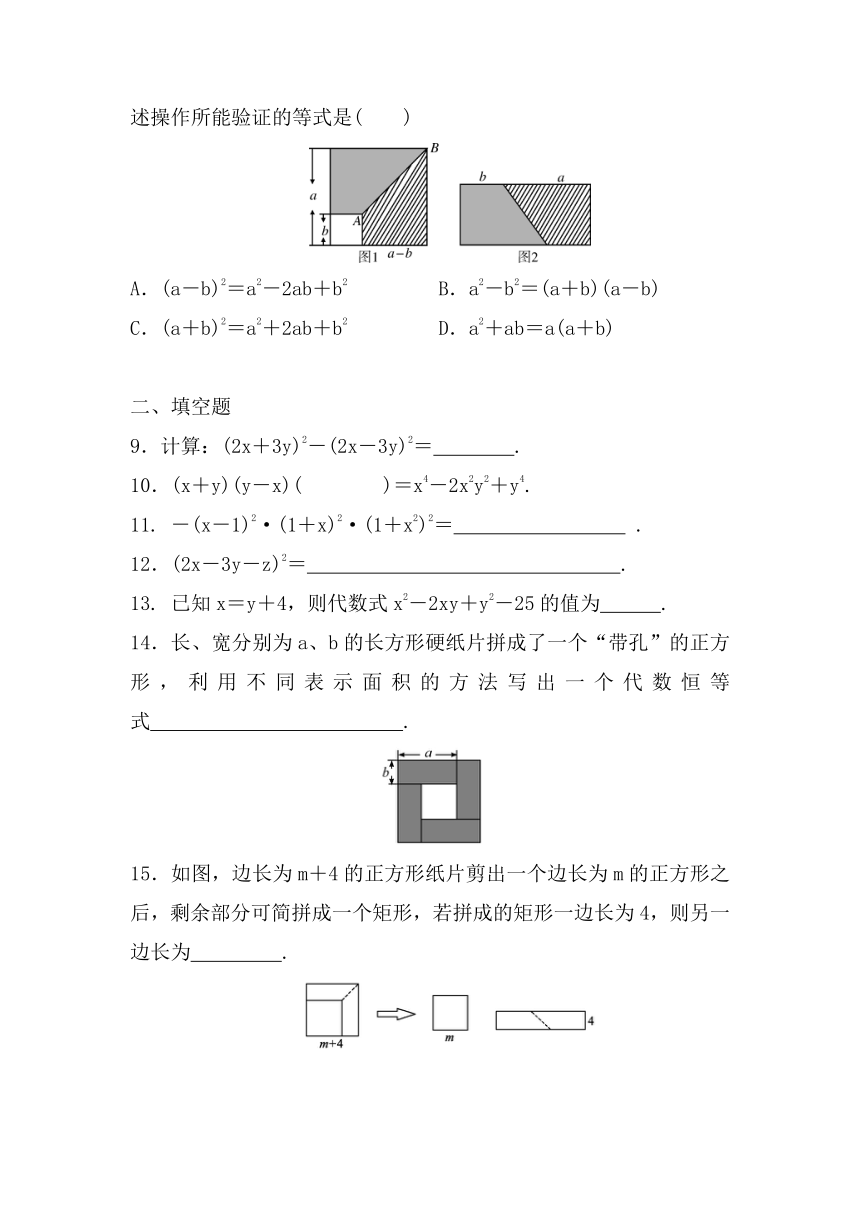
8. 如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图2的矩形,上述操作所能验证的等式是( )
A.(a-b)2=a2-2ab+b2 B.a2-b2=(a+b)(a-b)
C.(a+b)2=a2+2ab+b2 D.a2+ab=a(a+b)
二、填空题
9.计算:(2x+3y)2-(2x-3y)2= .
10.(x+y)(y-x)( )=x4-2x2y2+y4.
11. -(x-1)2·(1+x)2·(1+x2)2= .
12.(2x-3y-z)2= .
13. 已知x=y+4,则代数式x2-2xy+y2-25的值为 .
14.长、宽分别为a、b的长方形硬纸片拼成了一个“带孔”的正方形,利用不同表示面积的方法写出一个代数恒等式 .
15.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可简拼成一个矩形,若拼成的矩形一边长为4,则另一边长为 .
三、解答题
16. 计算:
(1) (x+3)2(x-3)2;
(2) (x-2y)(x+2y)-(x+2y)2.
17. 化简:
(1) (3x+2y)2-3x(x+2y+2);
(2) 2a(a-1)2+a(3a+4)(3a-4).
18. 已知a2+b2+c2-2a+4b-6c+14=0,求c-a+b的值.
19. 先化简,再求值:
(1+a)(1-a)+a(a-2),其中a=.
20.若一个正方形的边长增加3cm,它的面积增加45cm2,求这个正方形原来的边长.
21. 先化简(a+1)(a-1)+a(1-a)-a,再根据化简结果,你发现该代数式的值与a的取值有什么关系?(不必说理)
22.一个正方形的边长增加3cm,它的面积就增加39cm2.求这个正方形的边长.
答案:
一、
1-8 CCCBB DAB
二、
9. 24xy
10. y2-x2
11. -x8+2x4-1
12. 4x2-4xz+9y2+z2+6yz-12xy
13. -9
14. (a+b)2-(a-b)2=4ab
15. 2m+4
三、
16. 解:(1)原式=[(x+3)(x-3)]2=(x2-9)2=x4-18x2+81;
(2)原式=x2-4y2-(x2+4xy+4y2)=x2-4y2-x2-4xy-4y2=-4xy-8y2.
17. 解: (1)原式=9x2+12xy+4y2-3x2-6xy-6x=6x2+6xy-6x+4y2;
(2)原式=2a(a2-2a+1)+a(9a2-16)=11a3-4a2-14a.
18. 解: ∵a2+b2+c2-2a+4b-6c+14=0,∴(a2-2a+1)+(b2+4b+4)+(c2-6c+9)=0,∴(a-1)2+(b+2)2+(c-3)2=0.又∵(a-1)2≥0,(b+2)2≥0,(c-3)2≥0,∴a=1,b=-2,c=3.∴c-a+b=3-1+(-2)=0.
19. 解:原式=1-2a,值为0
20. 解:设此正方形原来的边长为x,则x2+45=(x+3)2,解得x=6.
答:这个正方形原来的边长为6cm.
21. 解:原式=a2-1+a-a2-a=-1,该代数式的值与a的取值无关.
22. 解:设这个正方形的边长为xcm,根据题意得(x+3)2-x2=39,即6x+9=39,x=5,即正方形的边长是5cm.
一、选择题
1.下列计算正确的是( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2
C.(x+1)(x-1)=x2-1 D.(x-1)2=x2-1
2.如果(a+b)2-(a-b)2=4,则a和b的关系是( )
A.互为相反数 B.相等 C.互为倒数 D.互为负倒数
3.若a2-b2=-20,a-b=4,则a+b的值是( )
A.-4 B.5 C.-5 D.以上都不对
4.对于任意整数n,多项式(n+7)2-n2都能被( )
A.2整除 B.7整除 C.n整除 D.(n+7)整除
5.下列各式计算正确的是( )
A.(a+b)2=a2+b2 B.a·a2=a3 C.a8·a2=a16 D.a2+a3=a5
6.若实数x、y、z满足(x-z)2-4(x-y)(y-z)=0,则下列式子一定成立的是( )
A.x+y+z=0 B.x+y-2z=0 C.y+z-2x=0 D.z+x-2y=0
7. 设正方形的面积为S1cm2,长方形的面积为S2cm2,如果长方形的长比正方形的边长多3cm,宽比正方形的边长少3cm,则S1与S2的大小关系是( )
A.S1>S2 B.S1<S2 C.S1=S2 D.不能确定
8. 如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图2的矩形,上述操作所能验证的等式是( )
A.(a-b)2=a2-2ab+b2 B.a2-b2=(a+b)(a-b)
C.(a+b)2=a2+2ab+b2 D.a2+ab=a(a+b)
二、填空题
9.计算:(2x+3y)2-(2x-3y)2= .
10.(x+y)(y-x)( )=x4-2x2y2+y4.
11. -(x-1)2·(1+x)2·(1+x2)2= .
12.(2x-3y-z)2= .
13. 已知x=y+4,则代数式x2-2xy+y2-25的值为 .
14.长、宽分别为a、b的长方形硬纸片拼成了一个“带孔”的正方形,利用不同表示面积的方法写出一个代数恒等式 .
15.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可简拼成一个矩形,若拼成的矩形一边长为4,则另一边长为 .
三、解答题
16. 计算:
(1) (x+3)2(x-3)2;
(2) (x-2y)(x+2y)-(x+2y)2.
17. 化简:
(1) (3x+2y)2-3x(x+2y+2);
(2) 2a(a-1)2+a(3a+4)(3a-4).
18. 已知a2+b2+c2-2a+4b-6c+14=0,求c-a+b的值.
19. 先化简,再求值:
(1+a)(1-a)+a(a-2),其中a=.
20.若一个正方形的边长增加3cm,它的面积增加45cm2,求这个正方形原来的边长.
21. 先化简(a+1)(a-1)+a(1-a)-a,再根据化简结果,你发现该代数式的值与a的取值有什么关系?(不必说理)
22.一个正方形的边长增加3cm,它的面积就增加39cm2.求这个正方形的边长.
答案:
一、
1-8 CCCBB DAB
二、
9. 24xy
10. y2-x2
11. -x8+2x4-1
12. 4x2-4xz+9y2+z2+6yz-12xy
13. -9
14. (a+b)2-(a-b)2=4ab
15. 2m+4
三、
16. 解:(1)原式=[(x+3)(x-3)]2=(x2-9)2=x4-18x2+81;
(2)原式=x2-4y2-(x2+4xy+4y2)=x2-4y2-x2-4xy-4y2=-4xy-8y2.
17. 解: (1)原式=9x2+12xy+4y2-3x2-6xy-6x=6x2+6xy-6x+4y2;
(2)原式=2a(a2-2a+1)+a(9a2-16)=11a3-4a2-14a.
18. 解: ∵a2+b2+c2-2a+4b-6c+14=0,∴(a2-2a+1)+(b2+4b+4)+(c2-6c+9)=0,∴(a-1)2+(b+2)2+(c-3)2=0.又∵(a-1)2≥0,(b+2)2≥0,(c-3)2≥0,∴a=1,b=-2,c=3.∴c-a+b=3-1+(-2)=0.
19. 解:原式=1-2a,值为0
20. 解:设此正方形原来的边长为x,则x2+45=(x+3)2,解得x=6.
答:这个正方形原来的边长为6cm.
21. 解:原式=a2-1+a-a2-a=-1,该代数式的值与a的取值无关.
22. 解:设这个正方形的边长为xcm,根据题意得(x+3)2-x2=39,即6x+9=39,x=5,即正方形的边长是5cm.
