2021-2022学年人教版八年级数学下册《第16章二次根式》章末综合测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册《第16章二次根式》章末综合测试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 246.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 21:14:37 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学下册《第16章二次根式》章末综合测试题(附答案)
一.选择题(共10小题,满分40分)
1.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
2.下列二次根式中,与可以合并的二次根式是( )
A. B. C. D.
3.下列等式正确的是( )
A.()2=3 B.=﹣3 C.=3 D.(﹣)2=﹣3
4.若式子在实数范围内有意义,则x的取值范围是( )
A.x>1 B.x<1 C.x≥1 D.x≤1
5.要使+有意义,则x应满足( )
A.<x≤3 B.x≤3且x≠ C.<x<3 D.≤x≤3
6.如果m=﹣2,n=+2,那么m和n的关系是( )
A.互为相反数 B.互为倒数 C.相等 D.互为负倒数
7.已知,则的算术平方根是( )
A. B. C.±2 D.2
8.若2<a<3,则等于( )
A.5﹣2a B.1﹣2a C.2a﹣5 D.2a﹣1
9.如图、在一个长方形中无重叠的放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )
A.(4﹣2)cm2 B.(8﹣4)cm2 C.(8﹣12)cm2 D.8cm2
10.已知是整数,正整数n的最小值为( )
A.96 B.6 C.24 D.2
二.填空题(共6小题,满分30分)
11.计算:= .
12.一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的面积是 cm2.
13.已知在数轴上的位置如图所示,化简:++= .
14.已知x=+1,y=﹣1,则x2﹣y2的值为 .
15.已知:,则ab3+a3b的值为 .
16.已知a,b为实数,ab=3,a+b=﹣6.
(1)a2b+ab2= ;
(2)a+b= .
三.解答题(共6小题,满分50分)
17.计算:
(1)+;
(2)(﹣+)÷.
18.计算:
(1);
(2).
19.阅读下列材料:我们在学习二次根式时,式子有意义,则x≥0;式子有意义,则x≤0;若式子+有意义,求x的取值范围.这个问题可以转化为不等式组来解决,即求关于x的不等式组的解集,解这个不等式组,得x=0.请你运用上述的数学方法解决下列问题:
(1)式子+有意义,求x的取值范围.
(2)已知y=+﹣3,求xy的值.
20.设一个三角形的三边长分别为a、b、c,P=(a+b+c),则有下列面积公式:S=(海伦公式).
(1)一个三角形边长依次为5、6、7,利用海伦公式求这个三角形的面积;
(2)一个三角形边长依次为2、、3,利用海伦公式求这个三角形的面积.
21.材料阅读:二次根式的运算中,经常会出现诸如,的计算,需要运用分式的基本性质,将分母转化为有理数,这就是“分母有理化”,例如:;.
类似地,将分子转化为有理数,就称为“分子有理化”,例如:;.
根据上述知识,请你完成下列问题:
(1)化简:;
(2)比较与的大小,并说明理由;
(3)计算:的值.
22.观察下列一组等式,解答后面的问题:
;
=;
(1)化简:= ,= (n为正整数),
(2)比较大小: ;(填“>”,“<”或“=”)
(3)根据上面的结论,找规律,请直接写出下列算式的结果:= .
参考答案
一.选择题(共10小题,满分40分)
1.解:A、=2,所以不是最简二次根式;
B、==,所以不是最简二次根式;
C、=5,所以不是最简二次根式;
D、是最简二次根式.
故选:D.
2.解:A、原式=,不符合题意;
B、原式=3,符合题意;
C、原式=,不符合题意;
D、原式=3,不符合题意.
故选:B.
3.解:A.()2=3,故A正确;
B.=3,故B错误;
C.=,故C错误;
D.(﹣)2=3,故D错误;
故选:A.
4.解:由题意得:1﹣x>0,
解得:x<1,
故选:B.
5.解:∵有意义,
∴3﹣x≥0且3x﹣1≠0,
∴x≤3且x≠,
故选:B.
6.解:m+n=﹣2=2,
mn=,
∴m和n互为倒数,
故选:B.
7.解:由题意得:b﹣8≥0,8﹣b≥0,
解得:b=8,
则a=2,
∴==4,
∵4的算术平方根是2,
∴的算术平方根是2,
故选:D.
8.解:∵2<a<3,
∴
=a﹣2﹣(3﹣a)
=a﹣2﹣3+a
=2a﹣5.
故选:C.
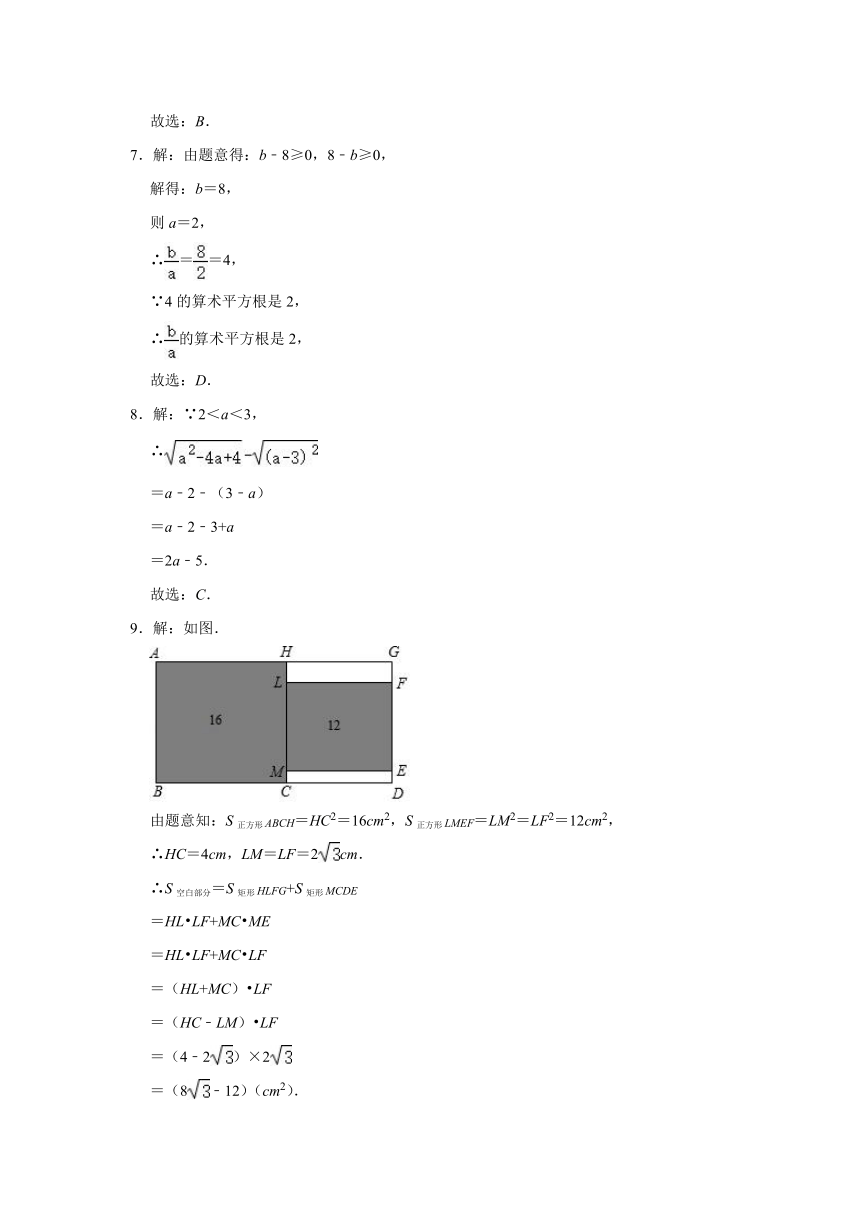
9.解:如图.
由题意知:S正方形ABCH=HC2=16cm2,S正方形LMEF=LM2=LF2=12cm2,
∴HC=4cm,LM=LF=2cm.
∴S空白部分=S矩形HLFG+S矩形MCDE
=HL LF+MC ME
=HL LF+MC LF
=(HL+MC) LF
=(HC﹣LM) LF
=(4﹣2)×2
=(8﹣12)(cm2).
故选:C.
10.解:96=42×6n,则是整数,
则正整数n的最小值6.
故选:B.
二.填空题(共6小题,满分30分)
11.解:原式=3﹣
=3﹣
=.
故答案为:.
12.解:这个直角三角形的面积=cm2,
故答案为:2
13.解:根据数轴得:n>0,m<n,m<﹣1,
∴m﹣n<0,m+1<0,
∴原式=n+n﹣m﹣(m+1)
=n+n﹣m﹣m﹣1
=2n﹣2m﹣1.
故答案为:2n﹣2m﹣1.
14.解:∵x=+1,y=﹣1,
∴x+y=+1+﹣1=2,
x﹣y=+1﹣+1=2,
则原式=(x+y)(x﹣y)
=2×2
=4,
故答案为:4.
15.解:∵,
∴a+b=+=,
ab=×==,
则原式=ab(a2+b2)
=ab[(a+b)2﹣2ab]
=×(3﹣2×)
=×
=,
故答案为:.
16.解:(1)原式=ab(a+b)
=3×(﹣6)
=﹣18;
(2)∵ab=3>0,
∴a,b同号,
又∵a+b=﹣6<0,
∴a<0,b<0.
原式=﹣(﹣a)﹣(﹣b)
=﹣﹣
=﹣﹣
=﹣2
=﹣2.
故答案为:(1)﹣18;(2)﹣2.
三.解答题(共6小题,满分50分)
17.解:(1)原式=﹣+
=﹣+
=3﹣2+5
=6;
(2)原式=(4﹣3+6)÷
=7÷
=7.
18.解:(1)原式=
=;
(2)原式=×(﹣)××
=﹣×
=﹣ ab3
=﹣ab2.
19.解:(1)∵+有意义
∴x2﹣1≥0,1﹣x2≤0,
∴x2=1,即x=±1.
(2)∵y=+﹣3有意义,
∴x﹣2≥0,2﹣x≥0.
∴x=2,
将x=2代入知y=+﹣3得y=﹣3.
∴xy=2﹣3=.
20.解:(1)P=(a+b+c)=(5+6+7)=9.
∴S==6.
(2)由题意:P=(2+3+)=.
∴P﹣a=,P﹣b=,p﹣c=.
∴S===.
21.解:(1)﹣
=﹣
=﹣
=﹣2﹣
=﹣2;
(2)﹣<﹣,
理由是:==+,==+,
∵+>+,
∴﹣<﹣;
(3)原式=++ +
=﹣1+﹣+ +﹣
=﹣1+
=﹣1+10
=9.
22.(1)==.
==.
故答案为:,
(2)==.
==.
∵<.
∴<.
故答案为:<.
(3)原式=++ +
=(++ +)
=
故答案为:.
一.选择题(共10小题,满分40分)
1.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
2.下列二次根式中,与可以合并的二次根式是( )
A. B. C. D.
3.下列等式正确的是( )
A.()2=3 B.=﹣3 C.=3 D.(﹣)2=﹣3
4.若式子在实数范围内有意义,则x的取值范围是( )
A.x>1 B.x<1 C.x≥1 D.x≤1
5.要使+有意义,则x应满足( )
A.<x≤3 B.x≤3且x≠ C.<x<3 D.≤x≤3
6.如果m=﹣2,n=+2,那么m和n的关系是( )
A.互为相反数 B.互为倒数 C.相等 D.互为负倒数
7.已知,则的算术平方根是( )
A. B. C.±2 D.2
8.若2<a<3,则等于( )
A.5﹣2a B.1﹣2a C.2a﹣5 D.2a﹣1
9.如图、在一个长方形中无重叠的放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )
A.(4﹣2)cm2 B.(8﹣4)cm2 C.(8﹣12)cm2 D.8cm2
10.已知是整数,正整数n的最小值为( )
A.96 B.6 C.24 D.2
二.填空题(共6小题,满分30分)
11.计算:= .
12.一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的面积是 cm2.
13.已知在数轴上的位置如图所示,化简:++= .
14.已知x=+1,y=﹣1,则x2﹣y2的值为 .
15.已知:,则ab3+a3b的值为 .
16.已知a,b为实数,ab=3,a+b=﹣6.
(1)a2b+ab2= ;
(2)a+b= .
三.解答题(共6小题,满分50分)
17.计算:
(1)+;
(2)(﹣+)÷.
18.计算:
(1);
(2).
19.阅读下列材料:我们在学习二次根式时,式子有意义,则x≥0;式子有意义,则x≤0;若式子+有意义,求x的取值范围.这个问题可以转化为不等式组来解决,即求关于x的不等式组的解集,解这个不等式组,得x=0.请你运用上述的数学方法解决下列问题:
(1)式子+有意义,求x的取值范围.
(2)已知y=+﹣3,求xy的值.
20.设一个三角形的三边长分别为a、b、c,P=(a+b+c),则有下列面积公式:S=(海伦公式).
(1)一个三角形边长依次为5、6、7,利用海伦公式求这个三角形的面积;
(2)一个三角形边长依次为2、、3,利用海伦公式求这个三角形的面积.
21.材料阅读:二次根式的运算中,经常会出现诸如,的计算,需要运用分式的基本性质,将分母转化为有理数,这就是“分母有理化”,例如:;.
类似地,将分子转化为有理数,就称为“分子有理化”,例如:;.
根据上述知识,请你完成下列问题:
(1)化简:;
(2)比较与的大小,并说明理由;
(3)计算:的值.
22.观察下列一组等式,解答后面的问题:
;
=;
(1)化简:= ,= (n为正整数),
(2)比较大小: ;(填“>”,“<”或“=”)
(3)根据上面的结论,找规律,请直接写出下列算式的结果:= .
参考答案
一.选择题(共10小题,满分40分)
1.解:A、=2,所以不是最简二次根式;
B、==,所以不是最简二次根式;
C、=5,所以不是最简二次根式;
D、是最简二次根式.
故选:D.
2.解:A、原式=,不符合题意;
B、原式=3,符合题意;
C、原式=,不符合题意;
D、原式=3,不符合题意.
故选:B.
3.解:A.()2=3,故A正确;
B.=3,故B错误;
C.=,故C错误;
D.(﹣)2=3,故D错误;
故选:A.
4.解:由题意得:1﹣x>0,
解得:x<1,
故选:B.
5.解:∵有意义,
∴3﹣x≥0且3x﹣1≠0,
∴x≤3且x≠,
故选:B.
6.解:m+n=﹣2=2,
mn=,
∴m和n互为倒数,
故选:B.
7.解:由题意得:b﹣8≥0,8﹣b≥0,
解得:b=8,
则a=2,
∴==4,
∵4的算术平方根是2,
∴的算术平方根是2,
故选:D.
8.解:∵2<a<3,
∴
=a﹣2﹣(3﹣a)
=a﹣2﹣3+a
=2a﹣5.
故选:C.
9.解:如图.
由题意知:S正方形ABCH=HC2=16cm2,S正方形LMEF=LM2=LF2=12cm2,
∴HC=4cm,LM=LF=2cm.
∴S空白部分=S矩形HLFG+S矩形MCDE
=HL LF+MC ME
=HL LF+MC LF
=(HL+MC) LF
=(HC﹣LM) LF
=(4﹣2)×2
=(8﹣12)(cm2).
故选:C.
10.解:96=42×6n,则是整数,
则正整数n的最小值6.
故选:B.
二.填空题(共6小题,满分30分)
11.解:原式=3﹣
=3﹣
=.
故答案为:.
12.解:这个直角三角形的面积=cm2,
故答案为:2
13.解:根据数轴得:n>0,m<n,m<﹣1,
∴m﹣n<0,m+1<0,
∴原式=n+n﹣m﹣(m+1)
=n+n﹣m﹣m﹣1
=2n﹣2m﹣1.
故答案为:2n﹣2m﹣1.
14.解:∵x=+1,y=﹣1,
∴x+y=+1+﹣1=2,
x﹣y=+1﹣+1=2,
则原式=(x+y)(x﹣y)
=2×2
=4,
故答案为:4.
15.解:∵,
∴a+b=+=,
ab=×==,
则原式=ab(a2+b2)
=ab[(a+b)2﹣2ab]
=×(3﹣2×)
=×
=,
故答案为:.
16.解:(1)原式=ab(a+b)
=3×(﹣6)
=﹣18;
(2)∵ab=3>0,
∴a,b同号,
又∵a+b=﹣6<0,
∴a<0,b<0.
原式=﹣(﹣a)﹣(﹣b)
=﹣﹣
=﹣﹣
=﹣2
=﹣2.
故答案为:(1)﹣18;(2)﹣2.
三.解答题(共6小题,满分50分)
17.解:(1)原式=﹣+
=﹣+
=3﹣2+5
=6;
(2)原式=(4﹣3+6)÷
=7÷
=7.
18.解:(1)原式=
=;
(2)原式=×(﹣)××
=﹣×
=﹣ ab3
=﹣ab2.
19.解:(1)∵+有意义
∴x2﹣1≥0,1﹣x2≤0,
∴x2=1,即x=±1.
(2)∵y=+﹣3有意义,
∴x﹣2≥0,2﹣x≥0.
∴x=2,
将x=2代入知y=+﹣3得y=﹣3.
∴xy=2﹣3=.
20.解:(1)P=(a+b+c)=(5+6+7)=9.
∴S==6.
(2)由题意:P=(2+3+)=.
∴P﹣a=,P﹣b=,p﹣c=.
∴S===.
21.解:(1)﹣
=﹣
=﹣
=﹣2﹣
=﹣2;
(2)﹣<﹣,
理由是:==+,==+,
∵+>+,
∴﹣<﹣;
(3)原式=++ +
=﹣1+﹣+ +﹣
=﹣1+
=﹣1+10
=9.
22.(1)==.
==.
故答案为:,
(2)==.
==.
∵<.
∴<.
故答案为:<.
(3)原式=++ +
=(++ +)
=
故答案为:.
