2021-2022学年人教版七年级数学下册《5-3平行线的性质》同步自主达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册《5-3平行线的性质》同步自主达标测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 21:16:10 | ||
图片预览


文档简介
2021-2022学年人教版七年级数学下册《5-3平行线的性质》同步自主达标测试(附答案)
一.选择题(共10小题,满分40分)
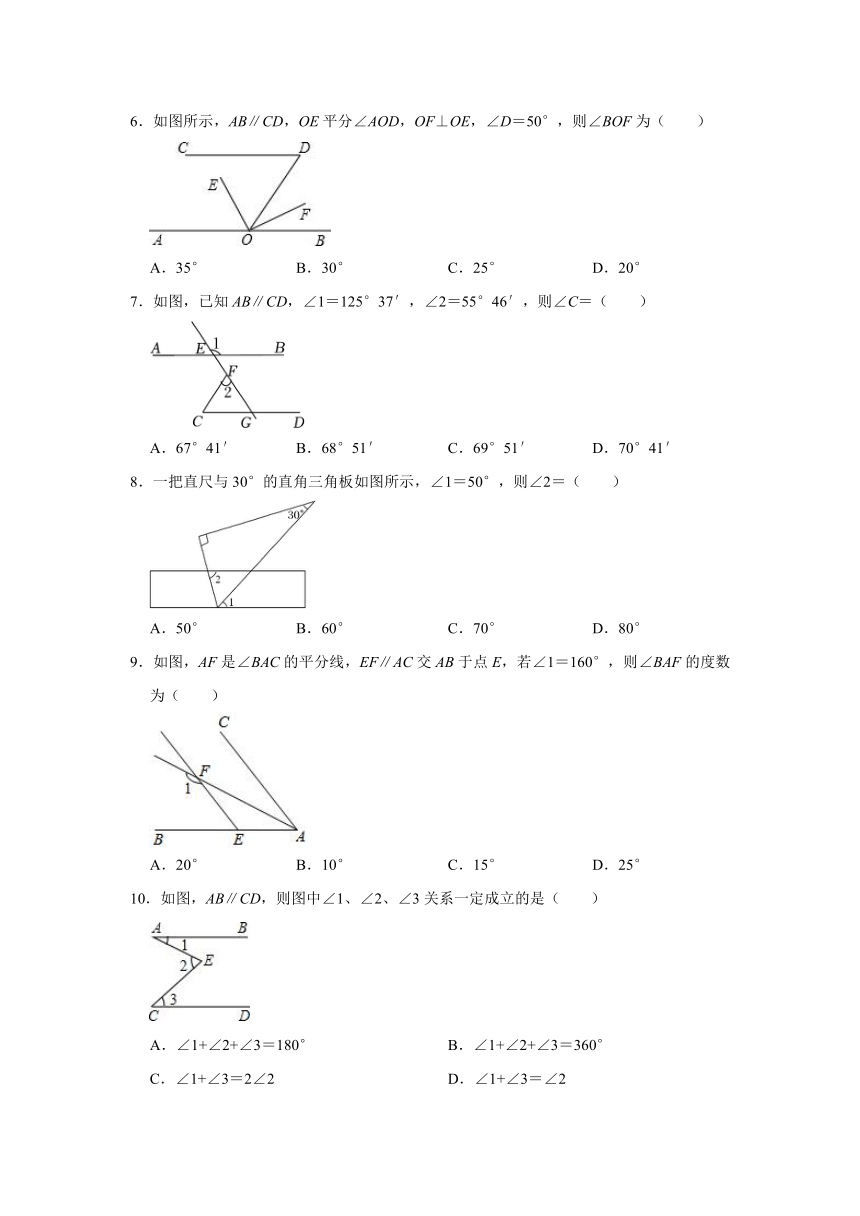
1.如图,直尺的一条边经过直角三角尺的直角顶点且平分直角,它的对边恰巧经过60°角的顶点.则∠1的大小是( )
A.30° B.45° C.60° D.105°
2.如图,AB∥CD,∠FGB=155°,FG平分∠EFD,则∠AEF的大小为( )
A.25° B.50° C.70° D.77.5°
3.如图,若要使l1与l2平行,则l1绕点O至少旋转的度数是( )
A.38° B.42° C.80° D.138°
4.如图,已知l1∥l2,∠A=45°,∠2=100°,则∠1的度数为( )
A.50° B.55° C.45° D.60°
5.如图,a∥b,c,d是截线,∠1=70°,∠2﹣∠3=30°,则∠4的大小是( )
A.100° B.105° C.110° D.120°
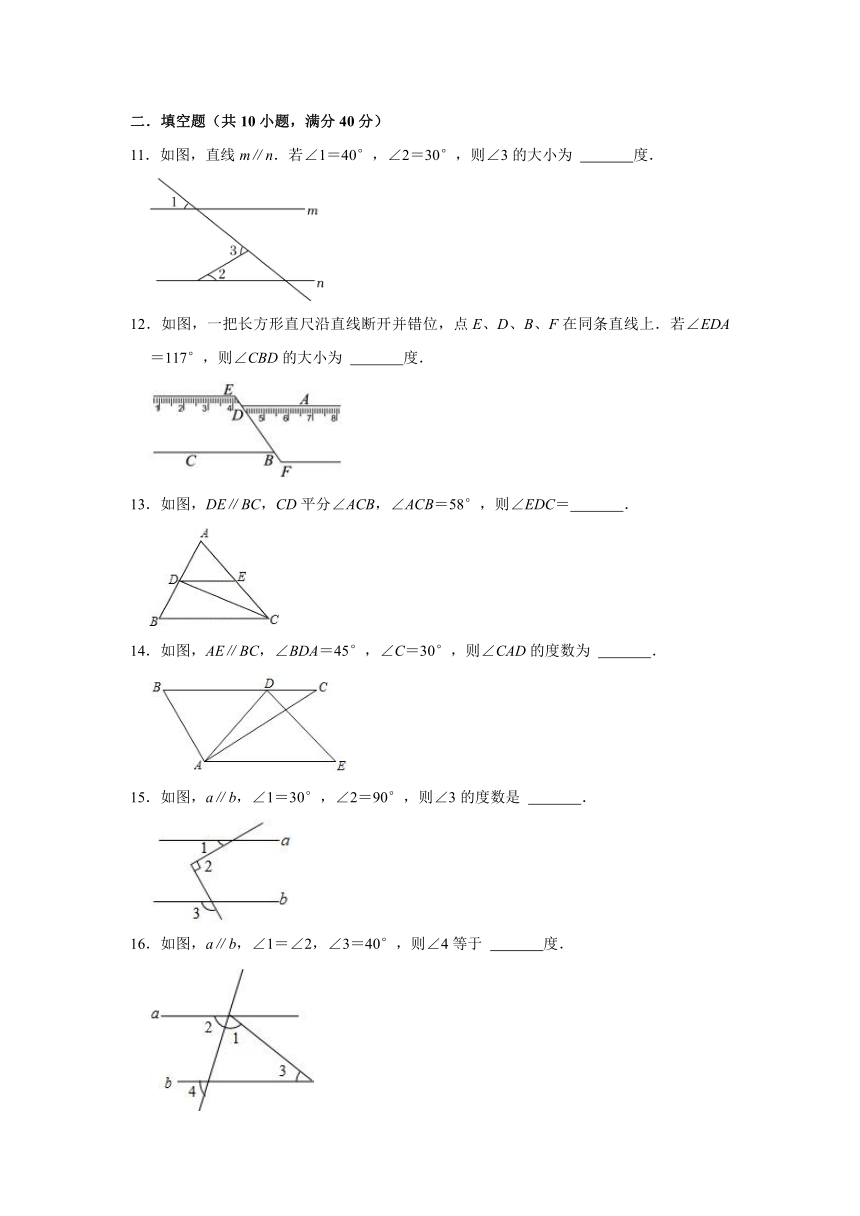
6.如图所示,AB∥CD,OE平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为( )
A.35° B.30° C.25° D.20°
7.如图,已知AB∥CD,∠1=125°37′,∠2=55°46′,则∠C=( )
A.67°41′ B.68°51′ C.69°51′ D.70°41′
8.一把直尺与30°的直角三角板如图所示,∠1=50°,则∠2=( )
A.50° B.60° C.70° D.80°
9.如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=160°,则∠BAF的度数为( )
A.20° B.10° C.15° D.25°
10.如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )
A.∠1+∠2+∠3=180° B.∠1+∠2+∠3=360°
C.∠1+∠3=2∠2 D.∠1+∠3=∠2
二.填空题(共10小题,满分40分)
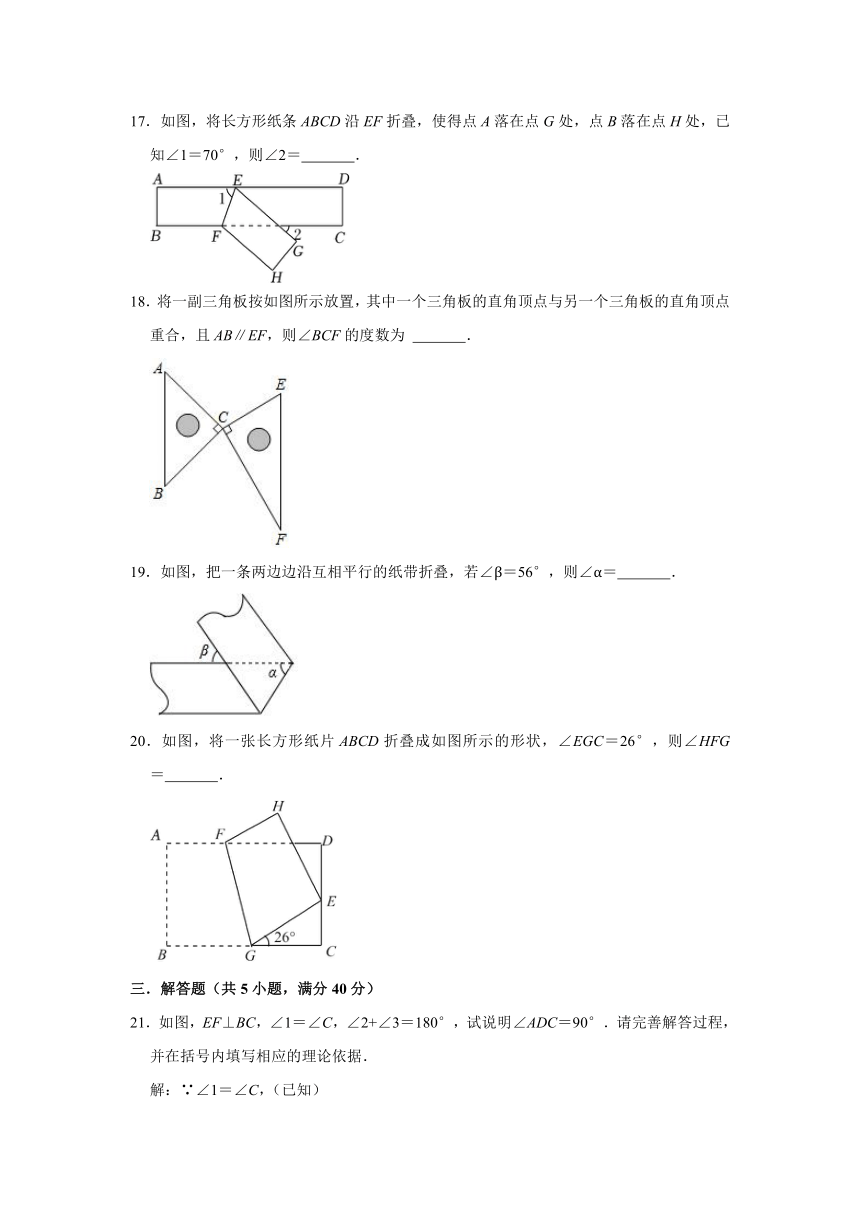
11.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为 度.
12.如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同条直线上.若∠EDA=117°,则∠CBD的大小为 度.
13.如图,DE∥BC,CD平分∠ACB,∠ACB=58°,则∠EDC= .
14.如图,AE∥BC,∠BDA=45°,∠C=30°,则∠CAD的度数为 .
15.如图,a∥b,∠1=30°,∠2=90°,则∠3的度数是 .
16.如图,a∥b,∠1=∠2,∠3=40°,则∠4等于 度.
17.如图,将长方形纸条ABCD沿EF折叠,使得点A落在点G处,点B落在点H处,已知∠1=70°,则∠2= .
18.将一副三角板按如图所示放置,其中一个三角板的直角顶点与另一个三角板的直角顶点重合,且AB∥EF,则∠BCF的度数为 .
19.如图,把一条两边边沿互相平行的纸带折叠,若∠β=56°,则∠α= .
20.如图,将一张长方形纸片ABCD折叠成如图所示的形状,∠EGC=26°,则∠HFG= .
三.解答题(共5小题,满分40分)
21.如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ . ( )
∴∠2=∠DAC. ( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. ( )
∴∠ADC=∠ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°. ( )
∴∠ADC=90°.(等量代换)
22.如图,已知AB∥DC,AC⊥BC,AC平分∠DAB,∠B=50°,求∠D的大小.
阅读下面的解答过程,并填括号里的空白(理由或数学式).
解:∵AB∥DC( ),
∴∠B+∠DCB=180°( ).
∵∠B= (已知),
∴∠DCB=180°﹣∠B=180°﹣50°=130°.
∵AC⊥BC(已知),
∴∠ACB= (垂直的定义).
∴∠2= .
∵AB∥DC(已知),
∴∠1= ( ).
∵AC平分∠DAB(已知),
∴∠DAB=2∠1= (角平分线的定义).
∵AB∥DC(已知),
∴ +∠DAB=180°(两条直线平行,同旁内角互补).
∴∠D=180°﹣∠DAB= .
23.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知),
∠ABC=∠1 ( ),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴( )+∠2=180°(等式的性质),
∴AB∥CD ( ).
又∵∠2+∠BCD=( °),
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D ( ),
∴BC∥DE ( ).
24.如图,A、B是直线MN上的两个点,且不重合,分别过点A、B作直线MN的垂线AC、BD,点C、D在直线MN的同侧.若∠CAE=65°,∠DBF=65°,则AC与BD平行吗?AE与BF平行吗?完成下面的解答过程,并填空(理由或数学式).
解:∵AC⊥MN,BD⊥MN( ),
∴AC∥BD( ).
∵AC⊥MN,
∴∠CAB=90°( ).
∴∠1+∠CAE=90°.
同理可得∠2+∠DBF=90°.
∵∠CAE=65°,∠DBF=65°,
∴∠CAE=( )=65°( ).
∴( )=∠2.
∴AE∥BF( ).
25.完成下面的证明
如图,点B在AG上,AG∥CD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AG∥CD(已知)
∴∠ABC=∠BCD( )
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD( )
∴ =∠BCF(等量代换)
∴BE∥CF( )
∴ =∠F( )
∵BE⊥AF(已知)
∴ =90°( )
∴∠F=90°.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵AC平分∠BAD,∠BAD=90°,
∴∠BAC=45°,
∵BD∥AC,
∴∠ABD=∠BAC=45°,∠BCA+∠CBD=180°,
∵∠CBD=∠ABD+∠ABC=45°+60°=105°,
∴∠BCA=75°,
∴∠1=105°,故选:D.
2.解:∵AB∥CD,
∴∠FGB+∠GFD=180°,∠FGB=155°,
∴∠GFD=180°﹣∠FGB=25°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=50°,
∵AB∥CD,
∴∠AEF=∠EFD=50°.故选:B.
3.解:若l1与l2平行,
则∠1和∠2相等,
∵∠2=42°,
∴∠1=42°,
∴若要使l1与l2平行,则l1绕点O至少旋转的度数是80°﹣42°=38°,故选:A.
4.解:∵∠2=100°,
∴∠ACB=180°﹣100°=80°,
∵∠A=45°,
∴∠ABC=180°﹣45°﹣80°=55°,
∵l1∥l2,
∴∠1=∠ABC=55°,
故选:B.
5.解:∠2=180°﹣∠1=180°﹣70°=110°,
∵∠2﹣∠3=30°,
∴∠3=∠2﹣30°=110°﹣30°=80°,
∵a∥b,
∴∠5=∠3=80°,
∴∠4=180°﹣∠5=180°﹣80°=100°.
故选:A.
6.解:∵AB∥CD,∠D=50°,
∴∠DOA=130°,∠DOB=50°,
∵OE平分∠AOD,
∴∠DOE=65°,
∵OF⊥OE,
∴∠DOF=25°,
∴∠BOF=25°,
故选:C.
7.解:∵AB∥CD,∠1=125°37′,
∴∠EGD=∠1=125°37',
∵∠EGD是△CFG的外角,∠2=55°46',
∴∠C=∠EGD﹣∠2=69°51',
故选:C.
8.解:∵∠P=90°,∠G=30°,
∴∠PFG=90°﹣∠G=60°,
∵∠1=50°,
∴∠EFC=∠1+∠PFG=110°,
∵AD∥BC,
∴∠2+∠EFC=180°,
∴∠2=180°﹣∠EFC=70°,
故选:C.
9.解:∵∠1=160°,
∴∠EAF=180°﹣∠1=20°,
又∵,EF∥AC,
∴∠CAF=∠EAF=20°,
∵AF是∠BAC的平分线,
∴∠BAF=∠CAF=20°,
故选:A.
10.解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠AEF=∠1,∠CEF=∠3,
∵∠2=∠AEF+∠CEF=∠1+∠3.
故选:D.
二.填空题(共10小题,满分40分)
11.解:如图,
∵m∥n.∠1=40°,
∴∠4=∠1=40°,
∵∠3是图中三角形的外角,∠2=30°,
∴∠3=∠2+∠4=70°.
故答案为:70.
12.解:∵AD∥CB,
∴∠ADF=∠CBD,
∵∠EDA+∠ADF=180°,
∴∠ADF=180°﹣∠EDA=180°﹣117°=63°,
∴∠CBD=63°.
故答案为:63.
13.解:∵CD平分∠ACB,∠ACB=58°,
∴∠ECD=∠ACB=29°,
∵DE∥BC,
∴∠EDC=∠ECD=29°.
故答案为:29°.
14.解:∵AE∥BC,∠BDA=45°,∠C=30°,
∴∠DAE=∠BDA=45°,∠CAE=∠C=30°,
∴∠CAD=∠DAE﹣∠CAE=45°﹣30°=15°.
故答案为:15°.
15.解:如图,反向延长∠2的边与a交于一点,
∵∠2=90°,
∴∠4=90°+∠1=120°,
∵a∥b,
∴∠3=∠4=120°,
故答案为:120°.
16.解:∵a∥b,
∴∠2+∠1+∠3=180°,
∵∠1=∠2,∠3=40°,
∴∠2=70°,
∴∠4=70°,
故答案为:70
17.解:由折叠可得∠FEG=∠1=70°,
∴∠DEG=180°﹣∠1﹣∠FEG=40°,
∵AD∥BC,
∴∠2=∠DEG=40°,
故答案为:40°.
18.解:过点C作CD∥AB,如图所示:
∵AB∥EF,CD∥AB,
∴CD∥EF,
∴∠B=∠BCD=45°,∠F=∠FCD=30°,
∴∠BCF=∠BCD+∠FCD=75°.
故答案为:75°.
19.解:如图所示:
∵纸片两边平行,
∴∠1=∠β=56°,
由折叠的性质得:2∠α+∠1=180°,
∴2∠α+56°=180°,
解得:∠α=62°.
故答案为:62°.
20.解:由折叠可得,∠BGF=∠BGE=×(180°﹣26°)=77°,
∵AD∥BC,
∴∠HFG=∠AFG=180°﹣77°=103°,
故答案为:103°.
三.解答题(共5小题,满分40分)
21.解:∵∠1=∠C,(已知)
∴GD∥AC. (同位角相等,两直线平行)
∴∠2=∠DAC. (两直线平行,内错角相等)
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. (同旁内角互补,两直线平行)
∴∠ADC=∠EFC. (两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°. (垂直定义)
∴∠ADC=90°.(等量代换)
故答案为:AC;同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;EFC;两直线平行,同位角相等;垂直定义.
22.解:∵AB∥DC( 已知),
∴∠B+∠DCB=180°( 两直线平行,同旁内角互补).
∵∠B=50°(已知),
∴∠DCB=180°﹣∠B=180°﹣50°=130°.
∵AC⊥BC(已知),
∴∠ACB=90°(垂直的定义).
∴∠2=40°.
∵AB∥DC(已知),
∴∠1=40°( 两直线平行,内错角相等).
∵AC平分∠DAB(已知),
∴∠DAB=2∠1=80°(角平分线的定义).
∵AB∥DC(已知),
∴∠ADC+∠DAB=180°(两条直线平行,同旁内角互补).
∴∠D=180°﹣∠DAB=100°.
故答案为:已知;两直线平行,同旁内角互补;50°;90°;40°;40°;两直线平行,内错角相等;80°;∠ADC;100°.
23.解∵∠1=60°(已知),
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行).
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行).
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
24.解:∵AC⊥MN,BD⊥MN(已知),
∴AC∥BD(在同一平面内,垂直于同一条直线的两条直线平行).
∵AC⊥MN,
∴∠CAB=90°(垂直的定义).
∴∠1+∠CAE=90°.
同理可得∠2+∠DBF=90°.
∵∠CAE=65°,∠DBF=65°,
∴∠CAE=∠DBF=65°(等量代换).
∴∠1=∠2.
∴AE∥BF(同位角相等,两直线平行).
故答案为:已知;在同一平面内,垂直于同一条直线的两条直线平行;垂直的定义;∠DBF,等量代换;∠1;同位角相等,两直线平行.
25.证明:∵AG∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵∠ABE=∠FCB(已知),
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB,
即∠EBC=∠FCD,
∵CF平分∠BCD(已知),
∴∠BCF=∠FCD(角平分线的定义),
∴∠EBC=∠BCF(等量代换),
∴BE∥CF(内错角相等,两直线平行),
∴∠BEF=∠F(两直线平行,内错角相等),
∵BE⊥AF(已知),
∴∠BEF=90°(垂直的定义),
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义.
一.选择题(共10小题,满分40分)
1.如图,直尺的一条边经过直角三角尺的直角顶点且平分直角,它的对边恰巧经过60°角的顶点.则∠1的大小是( )
A.30° B.45° C.60° D.105°
2.如图,AB∥CD,∠FGB=155°,FG平分∠EFD,则∠AEF的大小为( )
A.25° B.50° C.70° D.77.5°
3.如图,若要使l1与l2平行,则l1绕点O至少旋转的度数是( )
A.38° B.42° C.80° D.138°
4.如图,已知l1∥l2,∠A=45°,∠2=100°,则∠1的度数为( )
A.50° B.55° C.45° D.60°
5.如图,a∥b,c,d是截线,∠1=70°,∠2﹣∠3=30°,则∠4的大小是( )
A.100° B.105° C.110° D.120°
6.如图所示,AB∥CD,OE平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为( )
A.35° B.30° C.25° D.20°
7.如图,已知AB∥CD,∠1=125°37′,∠2=55°46′,则∠C=( )
A.67°41′ B.68°51′ C.69°51′ D.70°41′
8.一把直尺与30°的直角三角板如图所示,∠1=50°,则∠2=( )
A.50° B.60° C.70° D.80°
9.如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=160°,则∠BAF的度数为( )
A.20° B.10° C.15° D.25°
10.如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )
A.∠1+∠2+∠3=180° B.∠1+∠2+∠3=360°
C.∠1+∠3=2∠2 D.∠1+∠3=∠2
二.填空题(共10小题,满分40分)
11.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为 度.
12.如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同条直线上.若∠EDA=117°,则∠CBD的大小为 度.
13.如图,DE∥BC,CD平分∠ACB,∠ACB=58°,则∠EDC= .
14.如图,AE∥BC,∠BDA=45°,∠C=30°,则∠CAD的度数为 .
15.如图,a∥b,∠1=30°,∠2=90°,则∠3的度数是 .
16.如图,a∥b,∠1=∠2,∠3=40°,则∠4等于 度.
17.如图,将长方形纸条ABCD沿EF折叠,使得点A落在点G处,点B落在点H处,已知∠1=70°,则∠2= .
18.将一副三角板按如图所示放置,其中一个三角板的直角顶点与另一个三角板的直角顶点重合,且AB∥EF,则∠BCF的度数为 .
19.如图,把一条两边边沿互相平行的纸带折叠,若∠β=56°,则∠α= .
20.如图,将一张长方形纸片ABCD折叠成如图所示的形状,∠EGC=26°,则∠HFG= .
三.解答题(共5小题,满分40分)
21.如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ . ( )
∴∠2=∠DAC. ( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. ( )
∴∠ADC=∠ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°. ( )
∴∠ADC=90°.(等量代换)
22.如图,已知AB∥DC,AC⊥BC,AC平分∠DAB,∠B=50°,求∠D的大小.
阅读下面的解答过程,并填括号里的空白(理由或数学式).
解:∵AB∥DC( ),
∴∠B+∠DCB=180°( ).
∵∠B= (已知),
∴∠DCB=180°﹣∠B=180°﹣50°=130°.
∵AC⊥BC(已知),
∴∠ACB= (垂直的定义).
∴∠2= .
∵AB∥DC(已知),
∴∠1= ( ).
∵AC平分∠DAB(已知),
∴∠DAB=2∠1= (角平分线的定义).
∵AB∥DC(已知),
∴ +∠DAB=180°(两条直线平行,同旁内角互补).
∴∠D=180°﹣∠DAB= .
23.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知),
∠ABC=∠1 ( ),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴( )+∠2=180°(等式的性质),
∴AB∥CD ( ).
又∵∠2+∠BCD=( °),
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D ( ),
∴BC∥DE ( ).
24.如图,A、B是直线MN上的两个点,且不重合,分别过点A、B作直线MN的垂线AC、BD,点C、D在直线MN的同侧.若∠CAE=65°,∠DBF=65°,则AC与BD平行吗?AE与BF平行吗?完成下面的解答过程,并填空(理由或数学式).
解:∵AC⊥MN,BD⊥MN( ),
∴AC∥BD( ).
∵AC⊥MN,
∴∠CAB=90°( ).
∴∠1+∠CAE=90°.
同理可得∠2+∠DBF=90°.
∵∠CAE=65°,∠DBF=65°,
∴∠CAE=( )=65°( ).
∴( )=∠2.
∴AE∥BF( ).
25.完成下面的证明
如图,点B在AG上,AG∥CD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AG∥CD(已知)
∴∠ABC=∠BCD( )
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD( )
∴ =∠BCF(等量代换)
∴BE∥CF( )
∴ =∠F( )
∵BE⊥AF(已知)
∴ =90°( )
∴∠F=90°.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵AC平分∠BAD,∠BAD=90°,
∴∠BAC=45°,
∵BD∥AC,
∴∠ABD=∠BAC=45°,∠BCA+∠CBD=180°,
∵∠CBD=∠ABD+∠ABC=45°+60°=105°,
∴∠BCA=75°,
∴∠1=105°,故选:D.
2.解:∵AB∥CD,
∴∠FGB+∠GFD=180°,∠FGB=155°,
∴∠GFD=180°﹣∠FGB=25°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=50°,
∵AB∥CD,
∴∠AEF=∠EFD=50°.故选:B.
3.解:若l1与l2平行,
则∠1和∠2相等,
∵∠2=42°,
∴∠1=42°,
∴若要使l1与l2平行,则l1绕点O至少旋转的度数是80°﹣42°=38°,故选:A.
4.解:∵∠2=100°,
∴∠ACB=180°﹣100°=80°,
∵∠A=45°,
∴∠ABC=180°﹣45°﹣80°=55°,
∵l1∥l2,
∴∠1=∠ABC=55°,
故选:B.
5.解:∠2=180°﹣∠1=180°﹣70°=110°,
∵∠2﹣∠3=30°,
∴∠3=∠2﹣30°=110°﹣30°=80°,
∵a∥b,
∴∠5=∠3=80°,
∴∠4=180°﹣∠5=180°﹣80°=100°.
故选:A.
6.解:∵AB∥CD,∠D=50°,
∴∠DOA=130°,∠DOB=50°,
∵OE平分∠AOD,
∴∠DOE=65°,
∵OF⊥OE,
∴∠DOF=25°,
∴∠BOF=25°,
故选:C.
7.解:∵AB∥CD,∠1=125°37′,
∴∠EGD=∠1=125°37',
∵∠EGD是△CFG的外角,∠2=55°46',
∴∠C=∠EGD﹣∠2=69°51',
故选:C.
8.解:∵∠P=90°,∠G=30°,
∴∠PFG=90°﹣∠G=60°,
∵∠1=50°,
∴∠EFC=∠1+∠PFG=110°,
∵AD∥BC,
∴∠2+∠EFC=180°,
∴∠2=180°﹣∠EFC=70°,
故选:C.
9.解:∵∠1=160°,
∴∠EAF=180°﹣∠1=20°,
又∵,EF∥AC,
∴∠CAF=∠EAF=20°,
∵AF是∠BAC的平分线,
∴∠BAF=∠CAF=20°,
故选:A.
10.解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠AEF=∠1,∠CEF=∠3,
∵∠2=∠AEF+∠CEF=∠1+∠3.
故选:D.
二.填空题(共10小题,满分40分)
11.解:如图,
∵m∥n.∠1=40°,
∴∠4=∠1=40°,
∵∠3是图中三角形的外角,∠2=30°,
∴∠3=∠2+∠4=70°.
故答案为:70.
12.解:∵AD∥CB,
∴∠ADF=∠CBD,
∵∠EDA+∠ADF=180°,
∴∠ADF=180°﹣∠EDA=180°﹣117°=63°,
∴∠CBD=63°.
故答案为:63.
13.解:∵CD平分∠ACB,∠ACB=58°,
∴∠ECD=∠ACB=29°,
∵DE∥BC,
∴∠EDC=∠ECD=29°.
故答案为:29°.
14.解:∵AE∥BC,∠BDA=45°,∠C=30°,
∴∠DAE=∠BDA=45°,∠CAE=∠C=30°,
∴∠CAD=∠DAE﹣∠CAE=45°﹣30°=15°.
故答案为:15°.
15.解:如图,反向延长∠2的边与a交于一点,
∵∠2=90°,
∴∠4=90°+∠1=120°,
∵a∥b,
∴∠3=∠4=120°,
故答案为:120°.
16.解:∵a∥b,
∴∠2+∠1+∠3=180°,
∵∠1=∠2,∠3=40°,
∴∠2=70°,
∴∠4=70°,
故答案为:70
17.解:由折叠可得∠FEG=∠1=70°,
∴∠DEG=180°﹣∠1﹣∠FEG=40°,
∵AD∥BC,
∴∠2=∠DEG=40°,
故答案为:40°.
18.解:过点C作CD∥AB,如图所示:
∵AB∥EF,CD∥AB,
∴CD∥EF,
∴∠B=∠BCD=45°,∠F=∠FCD=30°,
∴∠BCF=∠BCD+∠FCD=75°.
故答案为:75°.
19.解:如图所示:
∵纸片两边平行,
∴∠1=∠β=56°,
由折叠的性质得:2∠α+∠1=180°,
∴2∠α+56°=180°,
解得:∠α=62°.
故答案为:62°.
20.解:由折叠可得,∠BGF=∠BGE=×(180°﹣26°)=77°,
∵AD∥BC,
∴∠HFG=∠AFG=180°﹣77°=103°,
故答案为:103°.
三.解答题(共5小题,满分40分)
21.解:∵∠1=∠C,(已知)
∴GD∥AC. (同位角相等,两直线平行)
∴∠2=∠DAC. (两直线平行,内错角相等)
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. (同旁内角互补,两直线平行)
∴∠ADC=∠EFC. (两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°. (垂直定义)
∴∠ADC=90°.(等量代换)
故答案为:AC;同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;EFC;两直线平行,同位角相等;垂直定义.
22.解:∵AB∥DC( 已知),
∴∠B+∠DCB=180°( 两直线平行,同旁内角互补).
∵∠B=50°(已知),
∴∠DCB=180°﹣∠B=180°﹣50°=130°.
∵AC⊥BC(已知),
∴∠ACB=90°(垂直的定义).
∴∠2=40°.
∵AB∥DC(已知),
∴∠1=40°( 两直线平行,内错角相等).
∵AC平分∠DAB(已知),
∴∠DAB=2∠1=80°(角平分线的定义).
∵AB∥DC(已知),
∴∠ADC+∠DAB=180°(两条直线平行,同旁内角互补).
∴∠D=180°﹣∠DAB=100°.
故答案为:已知;两直线平行,同旁内角互补;50°;90°;40°;40°;两直线平行,内错角相等;80°;∠ADC;100°.
23.解∵∠1=60°(已知),
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行).
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行).
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
24.解:∵AC⊥MN,BD⊥MN(已知),
∴AC∥BD(在同一平面内,垂直于同一条直线的两条直线平行).
∵AC⊥MN,
∴∠CAB=90°(垂直的定义).
∴∠1+∠CAE=90°.
同理可得∠2+∠DBF=90°.
∵∠CAE=65°,∠DBF=65°,
∴∠CAE=∠DBF=65°(等量代换).
∴∠1=∠2.
∴AE∥BF(同位角相等,两直线平行).
故答案为:已知;在同一平面内,垂直于同一条直线的两条直线平行;垂直的定义;∠DBF,等量代换;∠1;同位角相等,两直线平行.
25.证明:∵AG∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵∠ABE=∠FCB(已知),
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB,
即∠EBC=∠FCD,
∵CF平分∠BCD(已知),
∴∠BCF=∠FCD(角平分线的定义),
∴∠EBC=∠BCF(等量代换),
∴BE∥CF(内错角相等,两直线平行),
∴∠BEF=∠F(两直线平行,内错角相等),
∵BE⊥AF(已知),
∴∠BEF=90°(垂直的定义),
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义.
