27.2.2相似三角形的性质 课件(共29张PPT)
文档属性
| 名称 | 27.2.2相似三角形的性质 课件(共29张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 963.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 20:53:33 | ||
图片预览





文档简介
(共29张PPT)
27.2.2 相似三角形的性质
2021-2022学年九年级数学下册(人教版)
第二十七章 相似
学习目标
1.明确相似三角形中对应线段与相似比的关系.
(重点)
2.能熟练运用相似三角形的性质解决实际问题.(难点)
1、相似三角形有哪些判定方法?
(1)平行于三角形一边的直线和其他两边(或延长线)相交所 构成的三角形与原三角形相似
(2)三边成比例的两个三角形相似
(3)两边成比例且夹角相等的两个三角形相似
(4)两角分别相等的两个三角形相似
(5)斜边和一条直角边成比例的两个直角三角形相似
回顾旧知
A
C
B
A1
C1
B1
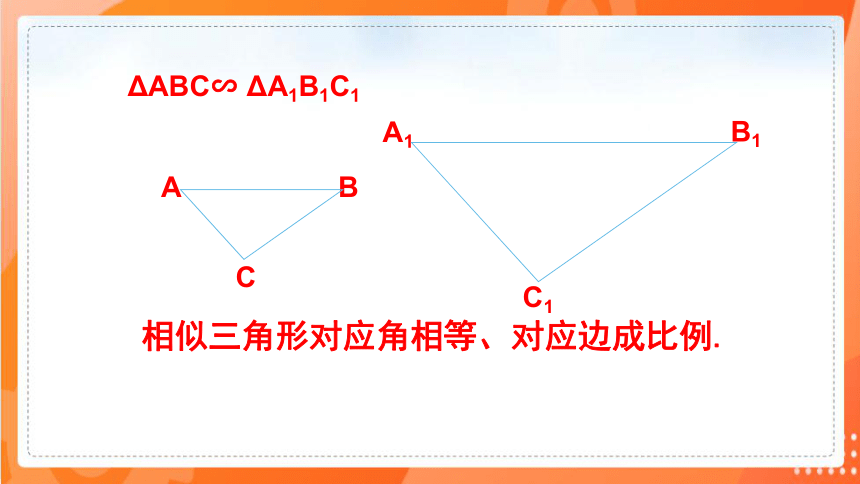
相似三角形对应角相等、对应边成比例.
ΔABC∽ ΔA1B1C1
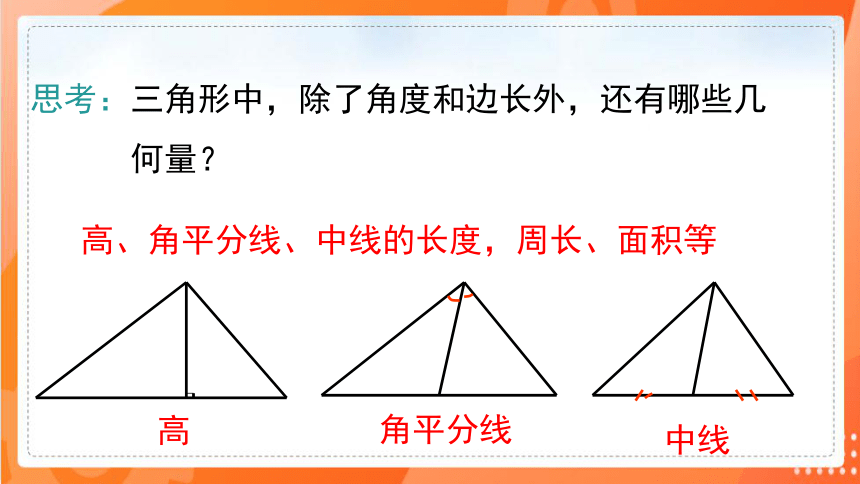
思考:三角形中,除了角度和边长外,还有哪些几
何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
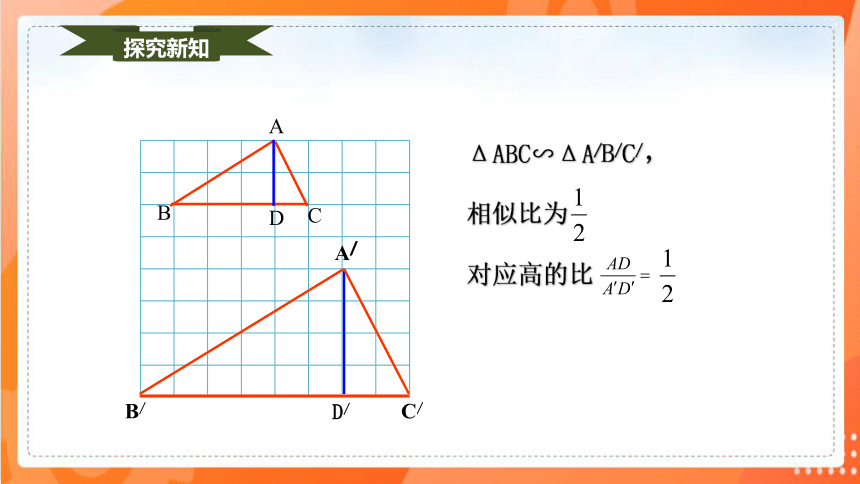
ΔABC∽ΔA/B/C/,
相似比为
对应高的比
A
B
D
C
A/
B/
C/
D/
探究新知
ΔABC∽ΔA/B/C/,
相似比为
对应中线的比
A
B
D
C
A/
B/
C/
D/
探究新知
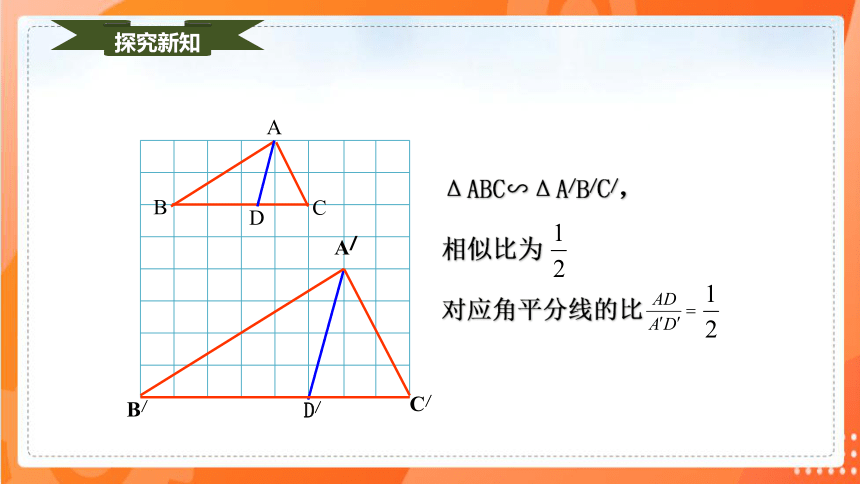
ΔABC∽ΔA/B/C/,
相似比为
对应角平分线的比
A
B
D
C
A/
B/
C/
D/
探究新知
可得:对应高的比
对应中线的比
对应角平分线的比
当ΔABC∽ΔA/B/C/,且相似比为 时
观察这些数据,你会有怎样的猜想呢?
猜想:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比
归纳
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
相似三角形的性质
相似比
=
一般地,相似三角形对应线段的比等于相似比
3.两个相似三角形对应中线的比为 ,
则对应高的比为______ .
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶ 3
1.两个相似三角形的相似比为 , 则对应高的比为_________, 则对应中线的比为_________.
巩固提高
4.ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
5.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分
线,已知AD=8cm, A1D1=3cm ,则 ΔABC与
ΔA1B1C1的对应高之比为 .
8:3
巩固提高
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
(相似三角形对应角平
线的比等于相似比),
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
巩固提高
问题:两个相似三角形的周长比会等于相似比吗?
合作探究 1
如图,分别为边长为1、2、3的等边三角形,它们相似吗?
(1)与(2)的相似比为 ;
(1)与(2)的周长比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的周长比为 。
结论:相似三角形的周长比等于 。
(1)
(2)
(3)
3
2
1
1:2
1:2
2:3
2:3
相似比
证明:∵△ABC∽△A′B′C′且相似比为k
∴
结论:相似三角形周长之比等于相似比
A
B
C
A /
B /
C /
已知△ABC∽△A′B′C′且相似比为k,
求证: △ABC的周长:△A′B′C′的周长=k
∴
∴
问题:两个相似三角形的面积之间有什么关系?
合作探究 2
结论:相似三角形的面积比等于 。
(1)与(2)的相似比为 ;
(1)与(2)的面积比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的面积比为 。
(1)
(2)
(3)
3
2
1
相似比平方
4:9
2:3
1:4
1:2
A
B
C
D
A /
B /
C /
D /
结论:相似三角形面积之比等于相似比的平方
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
相似比.
相似三角形面积的比=
相似三角形的性质
相似比的平方
=
归 纳
例1、如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF的周长和面积。
A
B
C
D
E
F
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
∴
又∠D=∠A,
∴△DEF∽△ABC,相似比为
∴△DEF的周长为
×24=12
面积为
例 题 讲 解
1.连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
2.两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长____cm,面积为____cm2.
1:2
1:4
14
巩固提高
3.判断:
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍.( )
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍.( )
√
×
巩固提高
4.如图, ABCD中,E为AD的中点,若 S ABCD=1,则图中阴影部分的面积为 ( )
A. B. C. D.
B
A
E
D
C
F
B
巩固提高
1、如图,△ABC是一块锐角三角形余料, 边BC=120毫米,高AD=80毫米,要把它加 工成正方形零件,使正方形的一边在BC上, 其余两个顶点分别在AB、AC上,这个正方 形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
AE
AD
=
PN
BC
因此 ,得 x=48(毫米)。
80–x
80
=
x
120
∵PN∥BC ∴△APN∽ △ABC
∴
应用拓展
2、如图,在△ABC中,D是AB的中点, DE∥BC则:
(1)S △ADE : S △ABC =
(2)S △ADE: S 梯形DBCE =
1:4
1:3
应用拓展
(1)相似三角形对应的 比等于相似比.
(3)相似 面积的比等于相似比的平方.
多边形
多边形
(2)相似 周长的比等于相似比.
三角形
三角形
高线
角平分线
中线
议一议:本节课你学到了什么?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
27.2.2 相似三角形的性质
2021-2022学年九年级数学下册(人教版)
第二十七章 相似
学习目标
1.明确相似三角形中对应线段与相似比的关系.
(重点)
2.能熟练运用相似三角形的性质解决实际问题.(难点)
1、相似三角形有哪些判定方法?
(1)平行于三角形一边的直线和其他两边(或延长线)相交所 构成的三角形与原三角形相似
(2)三边成比例的两个三角形相似
(3)两边成比例且夹角相等的两个三角形相似
(4)两角分别相等的两个三角形相似
(5)斜边和一条直角边成比例的两个直角三角形相似
回顾旧知
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
ΔABC∽ ΔA1B1C1
思考:三角形中,除了角度和边长外,还有哪些几
何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
ΔABC∽ΔA/B/C/,
相似比为
对应高的比
A
B
D
C
A/
B/
C/
D/
探究新知
ΔABC∽ΔA/B/C/,
相似比为
对应中线的比
A
B
D
C
A/
B/
C/
D/
探究新知
ΔABC∽ΔA/B/C/,
相似比为
对应角平分线的比
A
B
D
C
A/
B/
C/
D/
探究新知
可得:对应高的比
对应中线的比
对应角平分线的比
当ΔABC∽ΔA/B/C/,且相似比为 时
观察这些数据,你会有怎样的猜想呢?
猜想:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比
归纳
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
相似三角形的性质
相似比
=
一般地,相似三角形对应线段的比等于相似比
3.两个相似三角形对应中线的比为 ,
则对应高的比为______ .
2.相似三角形对应边的比为2∶3,那么对应角的角平分线的比为______.
2∶ 3
1.两个相似三角形的相似比为 , 则对应高的比为_________, 则对应中线的比为_________.
巩固提高
4.ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
5.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分
线,已知AD=8cm, A1D1=3cm ,则 ΔABC与
ΔA1B1C1的对应高之比为 .
8:3
巩固提高
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
(相似三角形对应角平
线的比等于相似比),
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
巩固提高
问题:两个相似三角形的周长比会等于相似比吗?
合作探究 1
如图,分别为边长为1、2、3的等边三角形,它们相似吗?
(1)与(2)的相似比为 ;
(1)与(2)的周长比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的周长比为 。
结论:相似三角形的周长比等于 。
(1)
(2)
(3)
3
2
1
1:2
1:2
2:3
2:3
相似比
证明:∵△ABC∽△A′B′C′且相似比为k
∴
结论:相似三角形周长之比等于相似比
A
B
C
A /
B /
C /
已知△ABC∽△A′B′C′且相似比为k,
求证: △ABC的周长:△A′B′C′的周长=k
∴
∴
问题:两个相似三角形的面积之间有什么关系?
合作探究 2
结论:相似三角形的面积比等于 。
(1)与(2)的相似比为 ;
(1)与(2)的面积比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的面积比为 。
(1)
(2)
(3)
3
2
1
相似比平方
4:9
2:3
1:4
1:2
A
B
C
D
A /
B /
C /
D /
结论:相似三角形面积之比等于相似比的平方
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
相似比.
相似三角形面积的比=
相似三角形的性质
相似比的平方
=
归 纳
例1、如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF的周长和面积。
A
B
C
D
E
F
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
∴
又∠D=∠A,
∴△DEF∽△ABC,相似比为
∴△DEF的周长为
×24=12
面积为
例 题 讲 解
1.连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
2.两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长____cm,面积为____cm2.
1:2
1:4
14
巩固提高
3.判断:
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍.( )
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍.( )
√
×
巩固提高
4.如图, ABCD中,E为AD的中点,若 S ABCD=1,则图中阴影部分的面积为 ( )
A. B. C. D.
B
A
E
D
C
F
B
巩固提高
1、如图,△ABC是一块锐角三角形余料, 边BC=120毫米,高AD=80毫米,要把它加 工成正方形零件,使正方形的一边在BC上, 其余两个顶点分别在AB、AC上,这个正方 形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
AE
AD
=
PN
BC
因此 ,得 x=48(毫米)。
80–x
80
=
x
120
∵PN∥BC ∴△APN∽ △ABC
∴
应用拓展
2、如图,在△ABC中,D是AB的中点, DE∥BC则:
(1)S △ADE : S △ABC =
(2)S △ADE: S 梯形DBCE =
1:4
1:3
应用拓展
(1)相似三角形对应的 比等于相似比.
(3)相似 面积的比等于相似比的平方.
多边形
多边形
(2)相似 周长的比等于相似比.
三角形
三角形
高线
角平分线
中线
议一议:本节课你学到了什么?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
