2021-2022学年北师大版数学七年级下册2.1两条直线的位置关系2课件(21张)
文档属性
| 名称 | 2021-2022学年北师大版数学七年级下册2.1两条直线的位置关系2课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 585.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 21:20:25 | ||
图片预览


文档简介
(共21张PPT)
第二章 相交线与平行线2
两直线相交的特殊情况——垂直
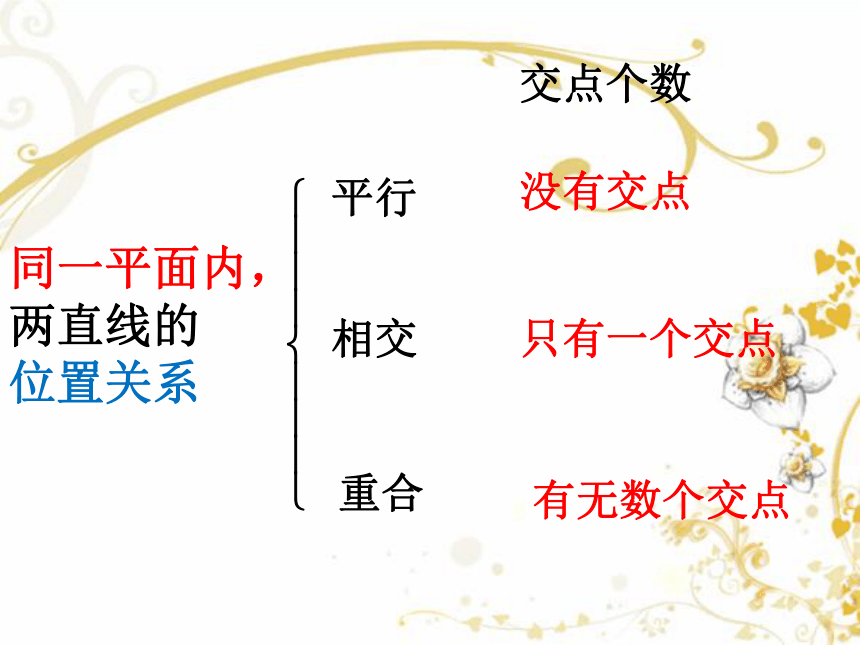
同一平面内,两直线的
位置关系
平行
相交
重合
交点个数
没有交点
只有一个交点
有无数个交点
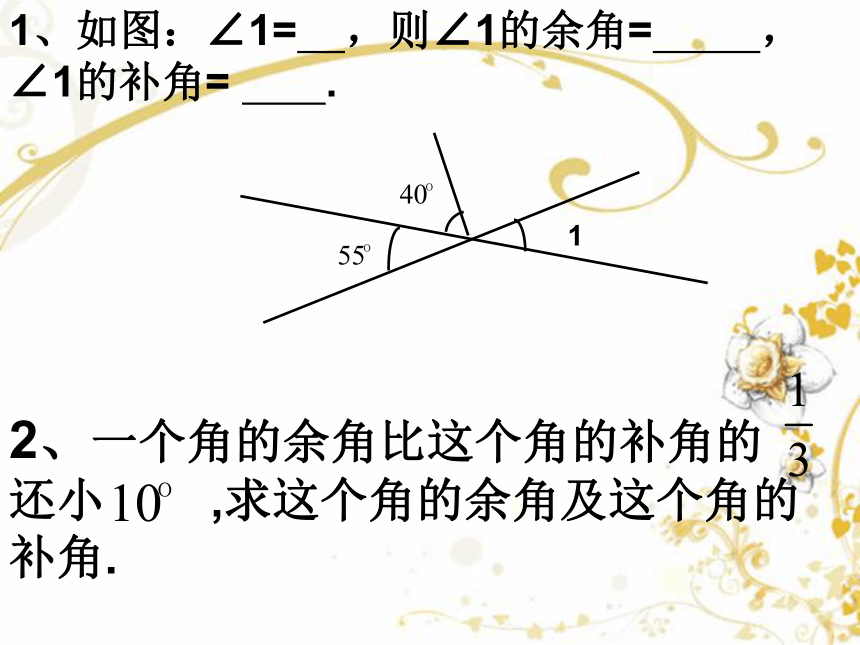
2、一个角的余角比这个角的补角的 还小 ,求这个角的余角及这个角的补角.
1、如图:∠1= ,则∠1的余角= ,
∠1的补角= .
1
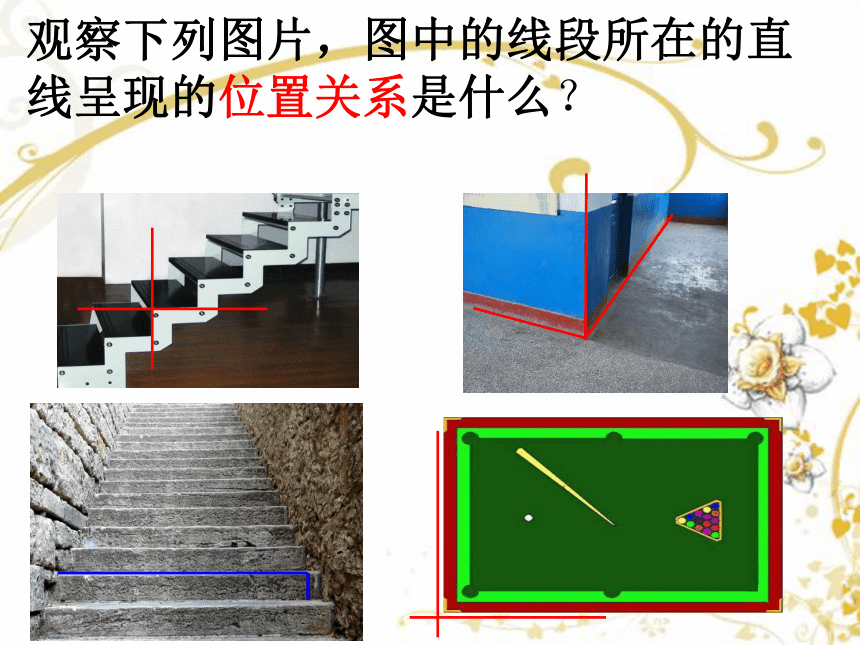
观察下列图片,图中的线段所在的直线呈现的位置关系是什么?
两条直线相交的一种特殊情况:垂直
特殊性1:相交所成的四个角都等于90°
特殊性4:记作:AB⊥CD (或 CD⊥AB),
垂足为点O
特殊性2:交点有专有名字:垂足
特殊性3:表示方法用
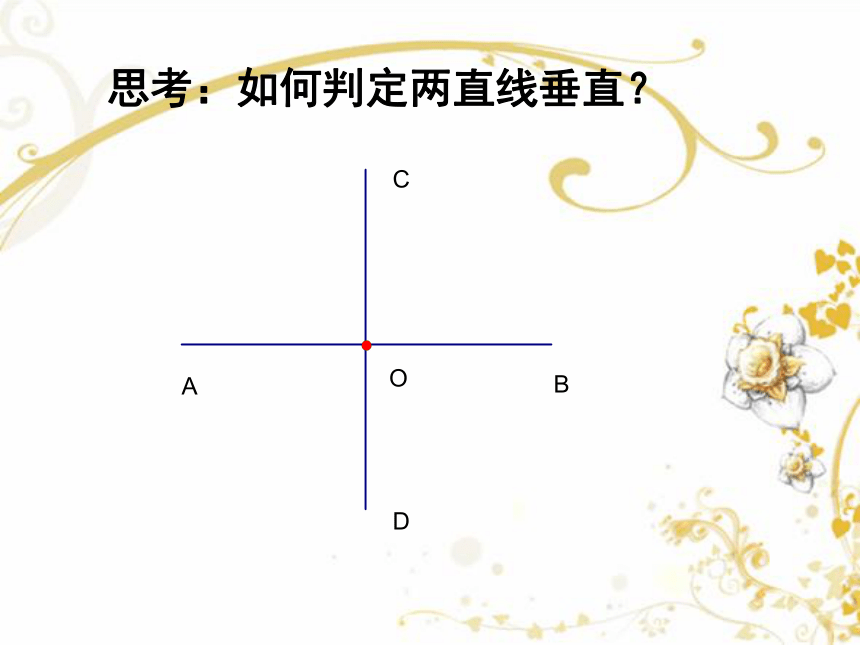
思考:如何判定两直线垂直?
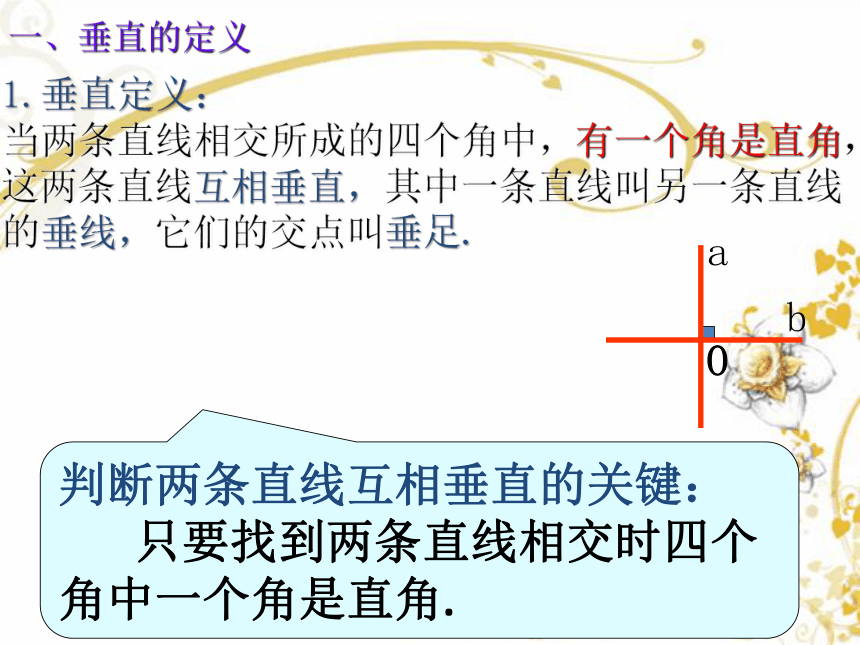
1.垂直定义:
当两条直线相交所成的四个角中,有一个角是直角,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
b
a
O
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个角中一个角是直角.
一、垂直的定义
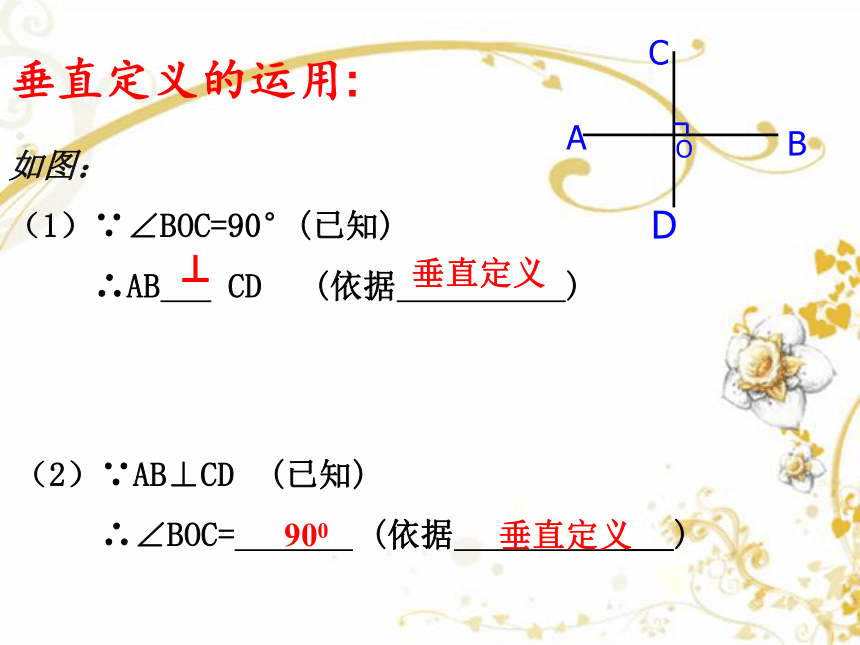
垂直定义的运用:
:
A
D
B
C
O
(2)∵AB⊥CD (已知)
∴∠BOC= (依据 ___)
如图:
(1)∵∠BOC=90°(已知)
∴AB CD (依据 )
⊥
垂直定义
垂直定义
900
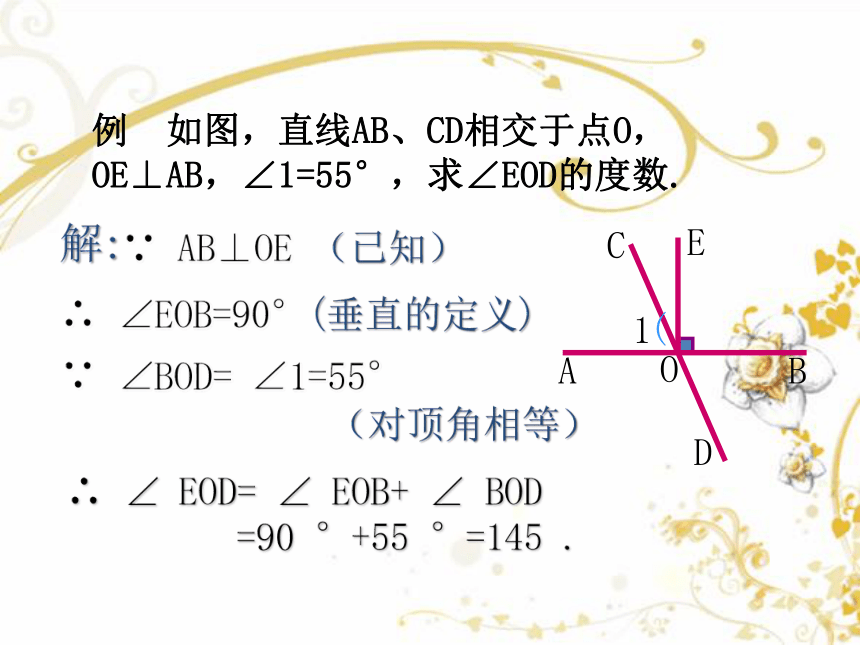
A
C
E
B
D
O
1
∴ ∠EOB=90°(垂直的定义)
∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 .
(
解:
∵ AB⊥OE (已知)
∵ ∠BOD= ∠1=55°
例 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
(对顶角相等)
问题:
直线n的垂线可以画几条?
n
O
m
无数条
问题1:
①你能借助三角尺,在一张白纸上画出两条互相垂直的直线吗?
动手画一画:
问题1:如图,过点A画直线m的垂线.
你能画出多少条?
.
m
A
.
A
m
.
A
m
结论:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线m和m上(或外)的一点A ,作m的垂线,可以作几条?
垂线的性质(一)
结论:
过一点(直线上或直线外)有且只有一条直线与已知直线垂直.
注意:
(1)“有且只有”中,“有”指存在,“只有”指唯一性.
(2)“过一点”中的点,可以在已知直线上,也可以在已知直线外.
(3)过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
垂线段最短
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
A
B
C
m
D
垂线段的长度
简单说成:垂线段最短.
垂线的性质(2)
问题2:
如图:已知∠ACB=90°若 BC=4cm, AC=3cm,AB=5cm,
1.点B到直线AC的距离等于 。
2.点A到直线BC的距离等于 。
3.你能求出点C到AB的距离吗?
C
B
A
D
第四环节
综合应用,开阔视野
C
A
B
如图,画出
(1)从村庄A到货场B怎样走最近?为什么?
(2)从货场B到铁道怎样走最近?为什么?
例1:如图,点O在直线AB上,OE⊥AB于点O,OC⊥OD,若∠DOE=320,请你求出∠EOC、∠BOD的度数,并说明理由。
A
O
B
D
C
E
例2:如图,点C在直线 AB上,过点C 引两条射线CE、CD,∠ACE=32°,∠DCB=58°,则CE、CD有何位置关系关系?为什么?
A
C
B
E
D
如图2.1—9中,点O在直线AB上,
OC平分∠BOD,OE平分∠AOD,
则OE和OC有何位置关系?
A
O
B
E
C
D
2.1--9
4. 如图:∠BAC=90°,AD⊥BC于点D,则下面结论中正确的有( )个。
①点B到AC的垂线段是线段AB;
②线段AC是点C到AB的垂线段;
③线段AD是点A到BC的垂线段;
④线段BD是点B到AD的垂线段。
A、1个;B、2个;C、3个;D、4个。
A
C
B
D
D
线段与线段垂直是指他们所在的直线垂直。
小结
1、垂直的概念:
如果两条直线相交所成的四个角中,有一个是直角,
就说这两条直线互相垂直.
2、同一平面内,经过一点有且只有一条直线与已知直 线垂直.画垂线的方法:用工具(量角器、三角板)
3、点到直线的距离:
从直线外一点到这条直线的垂线段的长度,叫做这个点到直线 的距离.
4、能过一点作出直线(或线段)的垂线(或垂线段),并能区别两点间的距离与点到直线的距离.
直线外一点与直线上各点的连线所有线段中,垂线段最短.
第二章 相交线与平行线2
两直线相交的特殊情况——垂直
同一平面内,两直线的
位置关系
平行
相交
重合
交点个数
没有交点
只有一个交点
有无数个交点
2、一个角的余角比这个角的补角的 还小 ,求这个角的余角及这个角的补角.
1、如图:∠1= ,则∠1的余角= ,
∠1的补角= .
1
观察下列图片,图中的线段所在的直线呈现的位置关系是什么?
两条直线相交的一种特殊情况:垂直
特殊性1:相交所成的四个角都等于90°
特殊性4:记作:AB⊥CD (或 CD⊥AB),
垂足为点O
特殊性2:交点有专有名字:垂足
特殊性3:表示方法用
思考:如何判定两直线垂直?
1.垂直定义:
当两条直线相交所成的四个角中,有一个角是直角,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
b
a
O
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个角中一个角是直角.
一、垂直的定义
垂直定义的运用:
:
A
D
B
C
O
(2)∵AB⊥CD (已知)
∴∠BOC= (依据 ___)
如图:
(1)∵∠BOC=90°(已知)
∴AB CD (依据 )
⊥
垂直定义
垂直定义
900
A
C
E
B
D
O
1
∴ ∠EOB=90°(垂直的定义)
∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 .
(
解:
∵ AB⊥OE (已知)
∵ ∠BOD= ∠1=55°
例 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
(对顶角相等)
问题:
直线n的垂线可以画几条?
n
O
m
无数条
问题1:
①你能借助三角尺,在一张白纸上画出两条互相垂直的直线吗?
动手画一画:
问题1:如图,过点A画直线m的垂线.
你能画出多少条?
.
m
A
.
A
m
.
A
m
结论:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线m和m上(或外)的一点A ,作m的垂线,可以作几条?
垂线的性质(一)
结论:
过一点(直线上或直线外)有且只有一条直线与已知直线垂直.
注意:
(1)“有且只有”中,“有”指存在,“只有”指唯一性.
(2)“过一点”中的点,可以在已知直线上,也可以在已知直线外.
(3)过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
垂线段最短
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
A
B
C
m
D
垂线段的长度
简单说成:垂线段最短.
垂线的性质(2)
问题2:
如图:已知∠ACB=90°若 BC=4cm, AC=3cm,AB=5cm,
1.点B到直线AC的距离等于 。
2.点A到直线BC的距离等于 。
3.你能求出点C到AB的距离吗?
C
B
A
D
第四环节
综合应用,开阔视野
C
A
B
如图,画出
(1)从村庄A到货场B怎样走最近?为什么?
(2)从货场B到铁道怎样走最近?为什么?
例1:如图,点O在直线AB上,OE⊥AB于点O,OC⊥OD,若∠DOE=320,请你求出∠EOC、∠BOD的度数,并说明理由。
A
O
B
D
C
E
例2:如图,点C在直线 AB上,过点C 引两条射线CE、CD,∠ACE=32°,∠DCB=58°,则CE、CD有何位置关系关系?为什么?
A
C
B
E
D
如图2.1—9中,点O在直线AB上,
OC平分∠BOD,OE平分∠AOD,
则OE和OC有何位置关系?
A
O
B
E
C
D
2.1--9
4. 如图:∠BAC=90°,AD⊥BC于点D,则下面结论中正确的有( )个。
①点B到AC的垂线段是线段AB;
②线段AC是点C到AB的垂线段;
③线段AD是点A到BC的垂线段;
④线段BD是点B到AD的垂线段。
A、1个;B、2个;C、3个;D、4个。
A
C
B
D
D
线段与线段垂直是指他们所在的直线垂直。
小结
1、垂直的概念:
如果两条直线相交所成的四个角中,有一个是直角,
就说这两条直线互相垂直.
2、同一平面内,经过一点有且只有一条直线与已知直 线垂直.画垂线的方法:用工具(量角器、三角板)
3、点到直线的距离:
从直线外一点到这条直线的垂线段的长度,叫做这个点到直线 的距离.
4、能过一点作出直线(或线段)的垂线(或垂线段),并能区别两点间的距离与点到直线的距离.
直线外一点与直线上各点的连线所有线段中,垂线段最短.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
