2021-2022学年鲁教版八年级数学下册《6-2矩形的性质与判定》同步练习题(Word版 附答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册《6-2矩形的性质与判定》同步练习题(Word版 附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 21:40:53 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学下册《1-2矩形的性质与判定》同步练习题(附答案)
1.一个长方形的三个顶点在平面直角坐标系中的坐标分别为(﹣1,﹣1),(﹣1,2),(3,﹣1),那么第四个顶点的坐标为( )
A.(3,2) B.(2,3) C.(3,3) D.(2,2)
2.四边形ABCD的对角线AC,BD,下面给出的三个条件中,选取两个,能使四边形ABCD是矩形,①AC,BD互相平分;②AC⊥BD;③AC=BD,则正确的选法是( )
A.①② B.①③ C.②③ D.以上都可以
3.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
4.如图,矩形ABCD中,点E是BC上一动点,连接AE、DE,以AE、DE为边作 AEDF,当点E从点B运动到点C的过程中, AEDF的面积( )
A.先变小后变大 B.先变大后变小
C.保持不变 D.一直变大
5.如图,在矩形ABCD中,AB=3,AD=5,点E在BC上,DF平分∠ADE,DE⊥EF,则BF长为( )
A. B.1 C. D.
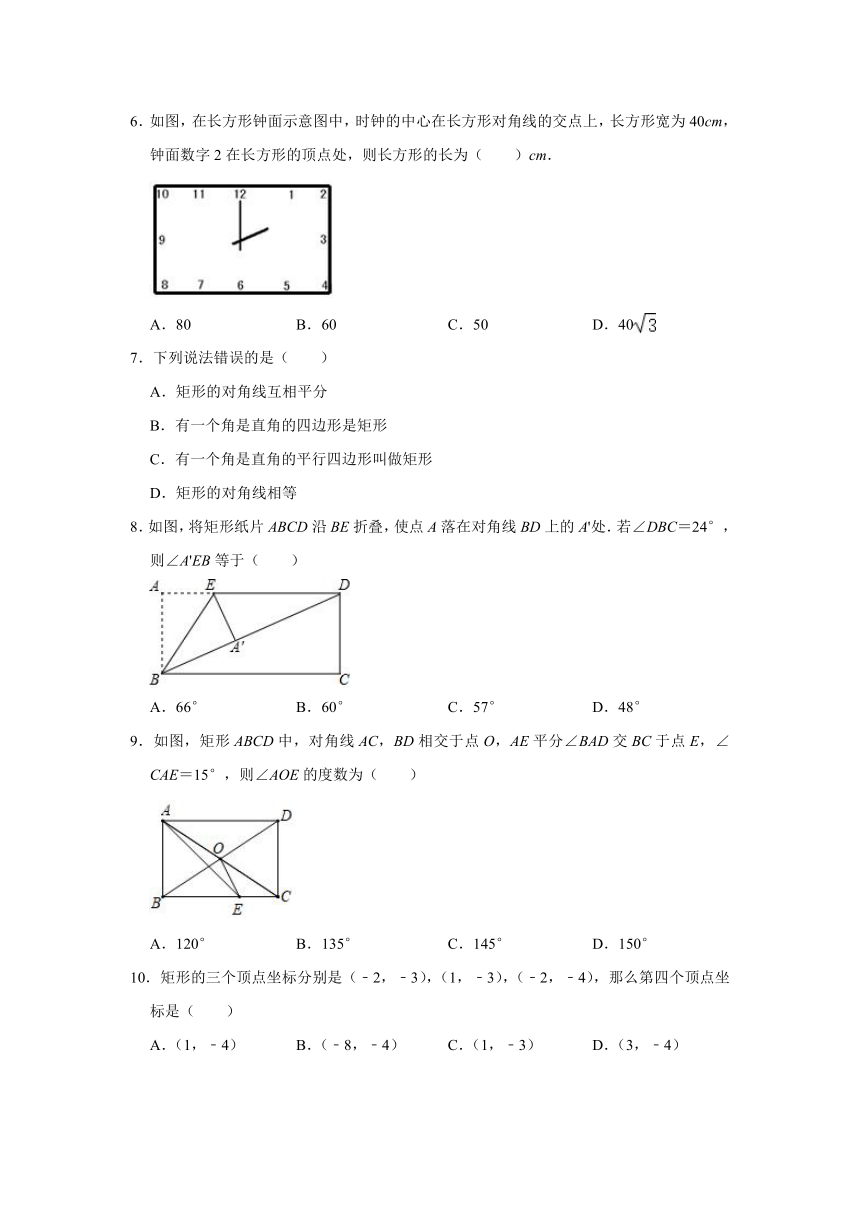
6.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为40cm,钟面数字2在长方形的顶点处,则长方形的长为( )cm.
A.80 B.60 C.50 D.40
7.下列说法错误的是( )
A.矩形的对角线互相平分
B.有一个角是直角的四边形是矩形
C.有一个角是直角的平行四边形叫做矩形
D.矩形的对角线相等
8.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
9.如图,矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,则∠AOE的度数为( )
A.120° B.135° C.145° D.150°
10.矩形的三个顶点坐标分别是(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),那么第四个顶点坐标是( )
A.(1,﹣4) B.(﹣8,﹣4) C.(1,﹣3) D.(3,﹣4)
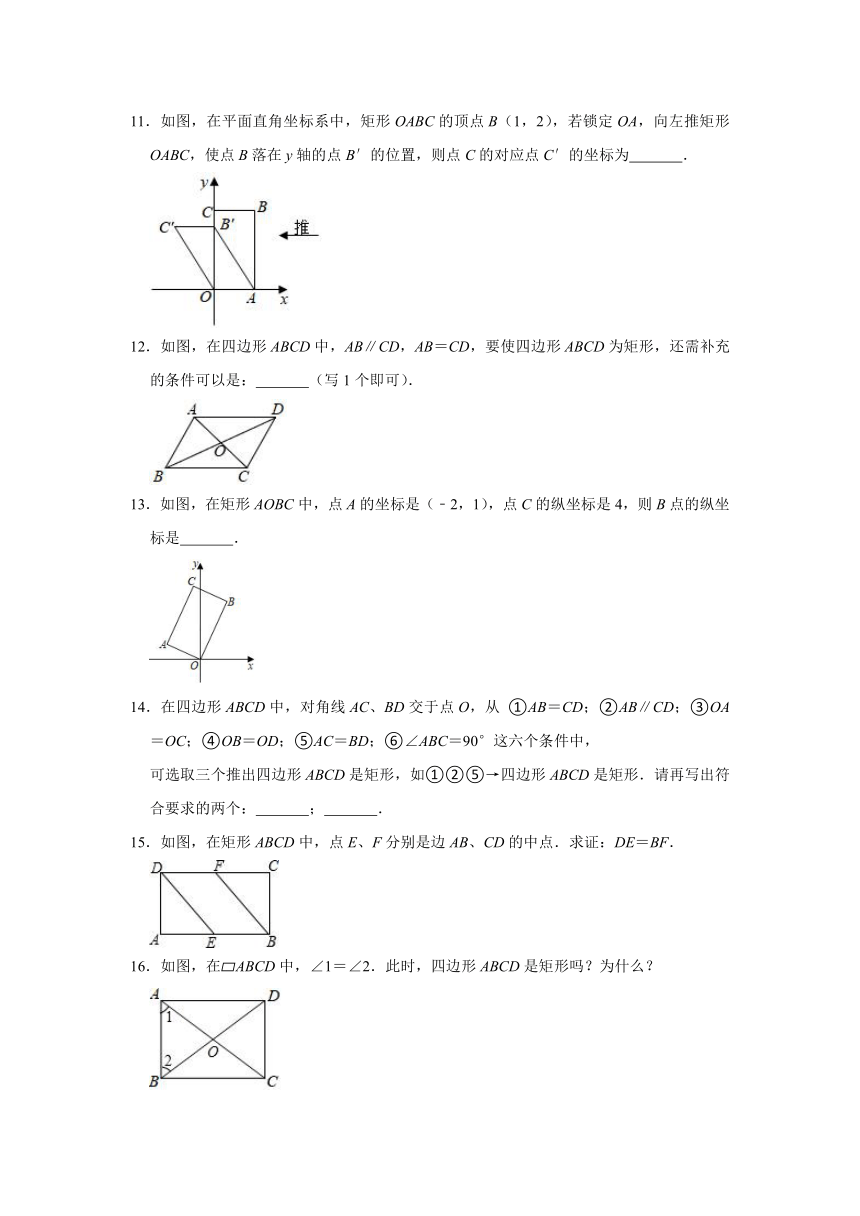
11.如图,在平面直角坐标系中,矩形OABC的顶点B(1,2),若锁定OA,向左推矩形OABC,使点B落在y轴的点B′的位置,则点C的对应点C′的坐标为 .
12.如图,在四边形ABCD中,AB∥CD,AB=CD,要使四边形ABCD为矩形,还需补充的条件可以是: (写1个即可).
13.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B点的纵坐标是 .
14.在四边形ABCD中,对角线AC、BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°这六个条件中,
可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个: ; .
15.如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.
16.如图,在 ABCD中,∠1=∠2.此时,四边形ABCD是矩形吗?为什么?
17.设矩形的一条对角线长为2cm,两条对角线组成的对顶角中,有一组是120°,求矩形的周长.
18.如图,在长方形ABCD中,点E在BC上,点F在CD上,且满足BE=CF=a,AB=EC=b.
(1)判断△AEF的形状,并证明你的结论;
(2)请用含a,b的代数式表示△AEF的面积;
(3)当△ABE的面积为24,BC长为14时,求△ADF的面积.
19.如图,在△ABC中,O是AC边上一点,过点O作BC的平行线,交∠BCA的平分线于点E,交外角∠ACD的平分线于点F.
(1)求证:EO=OF;
(2)连接AE,AF,当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由
20.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
参考答案
1.解:如图所示:
过(﹣1,2)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(﹣1,﹣1)和(3,2),
则第四个顶点坐标为(3,2),
故选:A.
2.解:当具备①③两个条件,能得到四边形ABCD是矩形.理由如下:
∵对角线AC、BD互相平分,
∴四边形ABCD为平行四边形.
又∵AC=BD,
∴四边形ABCD为矩形.
故选:B.
3.解:∵DE⊥BC,DF⊥AB,
∴∠DEB=∠DFB=90°,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ABC=90°,
∴四边形DEBF为矩形,
∴BF=DE=2.5,DF=EB,
设DF=3x,则EB=3x,
∵5DF=3AF,
∴AF=5x,AB=5x+2.5,
∵DE=2.5,
∴CE=3DE=7.5,
∴CB=7.5+3x,
∵AB=CB,
∴5x+2.5=7.5+3x,
解得x=2.5,
∴AF=5x=12.5,
故选:C.
4.解:过点E作EG⊥AD于G,如图所示:
则∠AGE=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠BAD=90°,
∴四边形ABEG是矩形,
∴EG=AB,
∵四边形AEDF是平行四边形,
∴平行四边形AEDF的面积=2△ADE的面积=2×AD×EG=AD×AB=矩形ABCD的面积,
即 AEDF的面积保持不变;
故选:C.
5.解:∵矩形ABCD中,DF平分∠ADE,DE⊥EF,
∴∠ADF=∠EDF,∠A=∠DEF=90°,
又∵DF=DF,
∴△ADF≌△EDF(AAS),
∴DE=DA=5,AF=EF,
∵四边形ABCD是矩形,
∴∠C=∠B=90°,CD=AB=3,BC=AD=5,
∴Rt△CDE中,CE==4,
∴BE=BC﹣CE=5﹣4=1,
设BF=x,则AF=EF=3﹣x,
∵Rt△BEF中,BE2+BF2=EF2,
∴12+x2=(3﹣x)2,
解得x=,
∴BF=,
故选:D.
6.解:由题意知∠AOC=2∠BOC,
∵∠AOC+∠BOC=90°,
∴∠BOC=30°,∠AOC=60°,
∴OB=BC,
∴矩形ABCD长是宽的倍,
∴长方形的长是40cm;
故选:D.
7.解:A、矩形的对角线互相平分;正确;
B、有一个角是直角的四边形是矩形;错误;
C、有一个角是直角的平行四边形叫做矩形;正确;
D、矩形的对角线相等;正确;
故选:B.
8.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
9.解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形中OA=OB,
∴△ABO是等边三角形,
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°,
∴∠BOE=(180°﹣30°)=75°,
∴∠AOE=∠AOB+∠BOE,
=60°+75°,
=135°.
故选:B.
10.解:如图所示:
∵矩形ABCD中,A、B、D三点的坐标分别(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),
∴点C的横坐标与B的横坐标相等,纵坐标与D的纵坐标相等,
即C的坐标是(1,﹣4).
故选:A.
11.解:∵四边形OABC是矩形,点B的坐标为(1,2),
∴OA=1,AB=2,
由题意得:AB'=AB=2,四边形OAB'C'是平行四边形,
∴OB'===,B'C'=OA=1,
∴点C的对应点C'的坐标为(﹣1,);
故答案为:(﹣1,).
12.解:还需补充的条件可以是:∠ABC=90°,理由如下:
∵AB∥CD,且AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故答案为:∠ABC=90°(答案不唯一).
13.解:如图,
过点A作AD⊥x轴于点D,
过点B作BE⊥x轴于点E,
过点C作CF∥y轴,过点A作AF∥x轴,交点为F,
则AF⊥CF,
延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴OB=AC,AC∥OB,
∴∠CAF=∠CHO=∠BOE,
∵∠AFC=∠OEB=90°,
∴△AFC≌△OEB(AAS),
∴CF=BE=4﹣1=3,
故答案为:3.
14.解:
①②⑥或③④⑥,
理由是:∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故答案为:①②⑥,③④⑥.
15.证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,又E、F分别是边AB、CD的中点,
∴DF=BE,又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE=BF.
16.解:四边形ABCD是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴OA=AC,OB=BD.
又∵∠1=∠2,
∴OA=OB,
∴AC=BD,
∴ ABCD是矩形.
17.解:如图所示:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OB=BD,AC=BD=2cm,
∴OA=OB=1cm,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=1cm,
∵在Rt△ABC中,∠ABC=90°,
∴BC===(cm),
∴矩形的周长=2AB+2BC=2×1cm+2×cm=(2+2)cm.
18.解:(1)△AEF是等腰直角三角形,理由如下:
∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°,AD=BC=a+b,
在△ABE和△ECF中,,
∴△ABE≌△ECF(SAS),
∴AE=EF,∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠CEF+∠AEB=90°,
∴∠AEF=90°,
∴△AEF是等腰直角三角形;
(2)∵∠B=90°,BE=CF=a,AB=CE=b,
∴AE2=AB2+BE2=a2+b2,
∴△AEF的面积=AE×EF=AE2=(a2+b2);
(3)∵△ABE的面积=24=ab,
∴ab=48,
∵BC=14,
∴a+b=14,
∴(a+b)2=142,
∴a2+2ab+b2=196,
∴a2+b2=100,
∴a2﹣2ab+b2=100﹣96=4,
即(a﹣b)2=4,
∵CD>FC,
∴b>a,
∴b﹣a=2,
∴△ADF的面积=AD×DF=BC×(b﹣a)=×14×2=14.
19.(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
又∵CE平分∠BCO,CF平分∠DCO,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形;理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,
即AC=EF,
∴平行四边形AECF是矩形,
即当点O沿AC移动时,四边形AECF能成为一个矩形,此时,点O在AC的中点.
20.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AD=10,
∴AD=AB=BC=10,
∵EC=4,
∴BE=10﹣4=6,
在Rt△ABE中,AE=,
在Rt△AEC中,AC=,
∵四边形ABCD是菱形,
∴OA=OC,
∴OE=AC=.
1.一个长方形的三个顶点在平面直角坐标系中的坐标分别为(﹣1,﹣1),(﹣1,2),(3,﹣1),那么第四个顶点的坐标为( )
A.(3,2) B.(2,3) C.(3,3) D.(2,2)
2.四边形ABCD的对角线AC,BD,下面给出的三个条件中,选取两个,能使四边形ABCD是矩形,①AC,BD互相平分;②AC⊥BD;③AC=BD,则正确的选法是( )
A.①② B.①③ C.②③ D.以上都可以
3.如图,在等腰直角△ABC中,AB=BC,点D是△ABC内部一点,DE⊥BC,DF⊥AB,垂足分别为E,F,若CE=3DE,5DF=3AF,DE=2.5,则AF=( )
A.8 B.10 C.12.5 D.15
4.如图,矩形ABCD中,点E是BC上一动点,连接AE、DE,以AE、DE为边作 AEDF,当点E从点B运动到点C的过程中, AEDF的面积( )
A.先变小后变大 B.先变大后变小
C.保持不变 D.一直变大
5.如图,在矩形ABCD中,AB=3,AD=5,点E在BC上,DF平分∠ADE,DE⊥EF,则BF长为( )
A. B.1 C. D.
6.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为40cm,钟面数字2在长方形的顶点处,则长方形的长为( )cm.
A.80 B.60 C.50 D.40
7.下列说法错误的是( )
A.矩形的对角线互相平分
B.有一个角是直角的四边形是矩形
C.有一个角是直角的平行四边形叫做矩形
D.矩形的对角线相等
8.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
9.如图,矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,则∠AOE的度数为( )
A.120° B.135° C.145° D.150°
10.矩形的三个顶点坐标分别是(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),那么第四个顶点坐标是( )
A.(1,﹣4) B.(﹣8,﹣4) C.(1,﹣3) D.(3,﹣4)
11.如图,在平面直角坐标系中,矩形OABC的顶点B(1,2),若锁定OA,向左推矩形OABC,使点B落在y轴的点B′的位置,则点C的对应点C′的坐标为 .
12.如图,在四边形ABCD中,AB∥CD,AB=CD,要使四边形ABCD为矩形,还需补充的条件可以是: (写1个即可).
13.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B点的纵坐标是 .
14.在四边形ABCD中,对角线AC、BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°这六个条件中,
可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个: ; .
15.如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.
16.如图,在 ABCD中,∠1=∠2.此时,四边形ABCD是矩形吗?为什么?
17.设矩形的一条对角线长为2cm,两条对角线组成的对顶角中,有一组是120°,求矩形的周长.
18.如图,在长方形ABCD中,点E在BC上,点F在CD上,且满足BE=CF=a,AB=EC=b.
(1)判断△AEF的形状,并证明你的结论;
(2)请用含a,b的代数式表示△AEF的面积;
(3)当△ABE的面积为24,BC长为14时,求△ADF的面积.
19.如图,在△ABC中,O是AC边上一点,过点O作BC的平行线,交∠BCA的平分线于点E,交外角∠ACD的平分线于点F.
(1)求证:EO=OF;
(2)连接AE,AF,当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由
20.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
参考答案
1.解:如图所示:
过(﹣1,2)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(﹣1,﹣1)和(3,2),
则第四个顶点坐标为(3,2),
故选:A.
2.解:当具备①③两个条件,能得到四边形ABCD是矩形.理由如下:
∵对角线AC、BD互相平分,
∴四边形ABCD为平行四边形.
又∵AC=BD,
∴四边形ABCD为矩形.
故选:B.
3.解:∵DE⊥BC,DF⊥AB,
∴∠DEB=∠DFB=90°,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ABC=90°,
∴四边形DEBF为矩形,
∴BF=DE=2.5,DF=EB,
设DF=3x,则EB=3x,
∵5DF=3AF,
∴AF=5x,AB=5x+2.5,
∵DE=2.5,
∴CE=3DE=7.5,
∴CB=7.5+3x,
∵AB=CB,
∴5x+2.5=7.5+3x,
解得x=2.5,
∴AF=5x=12.5,
故选:C.
4.解:过点E作EG⊥AD于G,如图所示:
则∠AGE=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠BAD=90°,
∴四边形ABEG是矩形,
∴EG=AB,
∵四边形AEDF是平行四边形,
∴平行四边形AEDF的面积=2△ADE的面积=2×AD×EG=AD×AB=矩形ABCD的面积,
即 AEDF的面积保持不变;
故选:C.
5.解:∵矩形ABCD中,DF平分∠ADE,DE⊥EF,
∴∠ADF=∠EDF,∠A=∠DEF=90°,
又∵DF=DF,
∴△ADF≌△EDF(AAS),
∴DE=DA=5,AF=EF,
∵四边形ABCD是矩形,
∴∠C=∠B=90°,CD=AB=3,BC=AD=5,
∴Rt△CDE中,CE==4,
∴BE=BC﹣CE=5﹣4=1,
设BF=x,则AF=EF=3﹣x,
∵Rt△BEF中,BE2+BF2=EF2,
∴12+x2=(3﹣x)2,
解得x=,
∴BF=,
故选:D.
6.解:由题意知∠AOC=2∠BOC,
∵∠AOC+∠BOC=90°,
∴∠BOC=30°,∠AOC=60°,
∴OB=BC,
∴矩形ABCD长是宽的倍,
∴长方形的长是40cm;
故选:D.
7.解:A、矩形的对角线互相平分;正确;
B、有一个角是直角的四边形是矩形;错误;
C、有一个角是直角的平行四边形叫做矩形;正确;
D、矩形的对角线相等;正确;
故选:B.
8.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
9.解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形中OA=OB,
∴△ABO是等边三角形,
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°,
∴∠BOE=(180°﹣30°)=75°,
∴∠AOE=∠AOB+∠BOE,
=60°+75°,
=135°.
故选:B.
10.解:如图所示:
∵矩形ABCD中,A、B、D三点的坐标分别(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),
∴点C的横坐标与B的横坐标相等,纵坐标与D的纵坐标相等,
即C的坐标是(1,﹣4).
故选:A.
11.解:∵四边形OABC是矩形,点B的坐标为(1,2),
∴OA=1,AB=2,
由题意得:AB'=AB=2,四边形OAB'C'是平行四边形,
∴OB'===,B'C'=OA=1,
∴点C的对应点C'的坐标为(﹣1,);
故答案为:(﹣1,).
12.解:还需补充的条件可以是:∠ABC=90°,理由如下:
∵AB∥CD,且AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故答案为:∠ABC=90°(答案不唯一).
13.解:如图,
过点A作AD⊥x轴于点D,
过点B作BE⊥x轴于点E,
过点C作CF∥y轴,过点A作AF∥x轴,交点为F,
则AF⊥CF,
延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴OB=AC,AC∥OB,
∴∠CAF=∠CHO=∠BOE,
∵∠AFC=∠OEB=90°,
∴△AFC≌△OEB(AAS),
∴CF=BE=4﹣1=3,
故答案为:3.
14.解:
①②⑥或③④⑥,
理由是:∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故答案为:①②⑥,③④⑥.
15.证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,又E、F分别是边AB、CD的中点,
∴DF=BE,又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE=BF.
16.解:四边形ABCD是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴OA=AC,OB=BD.
又∵∠1=∠2,
∴OA=OB,
∴AC=BD,
∴ ABCD是矩形.
17.解:如图所示:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OB=BD,AC=BD=2cm,
∴OA=OB=1cm,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=1cm,
∵在Rt△ABC中,∠ABC=90°,
∴BC===(cm),
∴矩形的周长=2AB+2BC=2×1cm+2×cm=(2+2)cm.
18.解:(1)△AEF是等腰直角三角形,理由如下:
∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°,AD=BC=a+b,
在△ABE和△ECF中,,
∴△ABE≌△ECF(SAS),
∴AE=EF,∠BAE=∠CEF,
∵∠BAE+∠AEB=90°,
∴∠CEF+∠AEB=90°,
∴∠AEF=90°,
∴△AEF是等腰直角三角形;
(2)∵∠B=90°,BE=CF=a,AB=CE=b,
∴AE2=AB2+BE2=a2+b2,
∴△AEF的面积=AE×EF=AE2=(a2+b2);
(3)∵△ABE的面积=24=ab,
∴ab=48,
∵BC=14,
∴a+b=14,
∴(a+b)2=142,
∴a2+2ab+b2=196,
∴a2+b2=100,
∴a2﹣2ab+b2=100﹣96=4,
即(a﹣b)2=4,
∵CD>FC,
∴b>a,
∴b﹣a=2,
∴△ADF的面积=AD×DF=BC×(b﹣a)=×14×2=14.
19.(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
又∵CE平分∠BCO,CF平分∠DCO,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形;理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,
即AC=EF,
∴平行四边形AECF是矩形,
即当点O沿AC移动时,四边形AECF能成为一个矩形,此时,点O在AC的中点.
20.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AD=10,
∴AD=AB=BC=10,
∵EC=4,
∴BE=10﹣4=6,
在Rt△ABE中,AE=,
在Rt△AEC中,AC=,
∵四边形ABCD是菱形,
∴OA=OC,
∴OE=AC=.
