2022年苏科版七年级数学下册7.5多边形的内角和与外角和训练(Word版 附答案)
文档属性
| 名称 | 2022年苏科版七年级数学下册7.5多边形的内角和与外角和训练(Word版 附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 258.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览



文档简介
7.5 多边形的内角和与外角和 提优训练
一、单选题
1.一个n边形的每个外角都是45°,则这个n边形的内角和是( )
A.1080° B.540° C.2700° D.2160°
2.一个多边形的外角和等于360°,则这个多边形的边数为( )
A.3 B.4
C.5 D.以上均有可能
3.如果一个多边形的外角和等于其内角和的2倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.如图,∠BDC=100°,∠C=35°,∠A=28°,则∠B的度数是( )
A.43° B.33° C.47° D.37°
5.如果一个多边形的内角和为,那么从这个多边形的一个顶点可以作( )条对角线.
A. B. C. D.
6.如图,在四边形中,,分别是两组对边延长线的交点,,分别是,的角平分线.若,,则( )
A. B. C. D.
7把一个正方形截去一个角后得到的多边形是
A. 三角形 B. 四边形 C. 五边形 D. 以上都有可能
8八边形一共有条对角线.
A. B. C. D.
9若一个多边形的内角和为,则从该多边形的一个顶点出发的对角线条数是
A. B. C. D.
10.(2020·江苏无锡市·七年级期中)图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
二、填空题
11.已知一个多边形的每个外角都是24°,此多边形是________边形.
12若一个正多边形的内角是外角的3倍还多20°,则这个多边形的边数是________.
13.如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于________.
14.(2021·陕西西安市·西北工业大学附属中学九年级一模)从正多边形一个顶点最多可以作7条对角线,这个正多边形每个内角的大小是_____.
15、通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是 度.
16、一个多边形的一个外角为α,且该多边形的内角和与α的和等于840°,则这个多边形的边数为 ,α= 度.
17、如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .
18.(2020·成都市金牛实验中学校七年级月考)如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
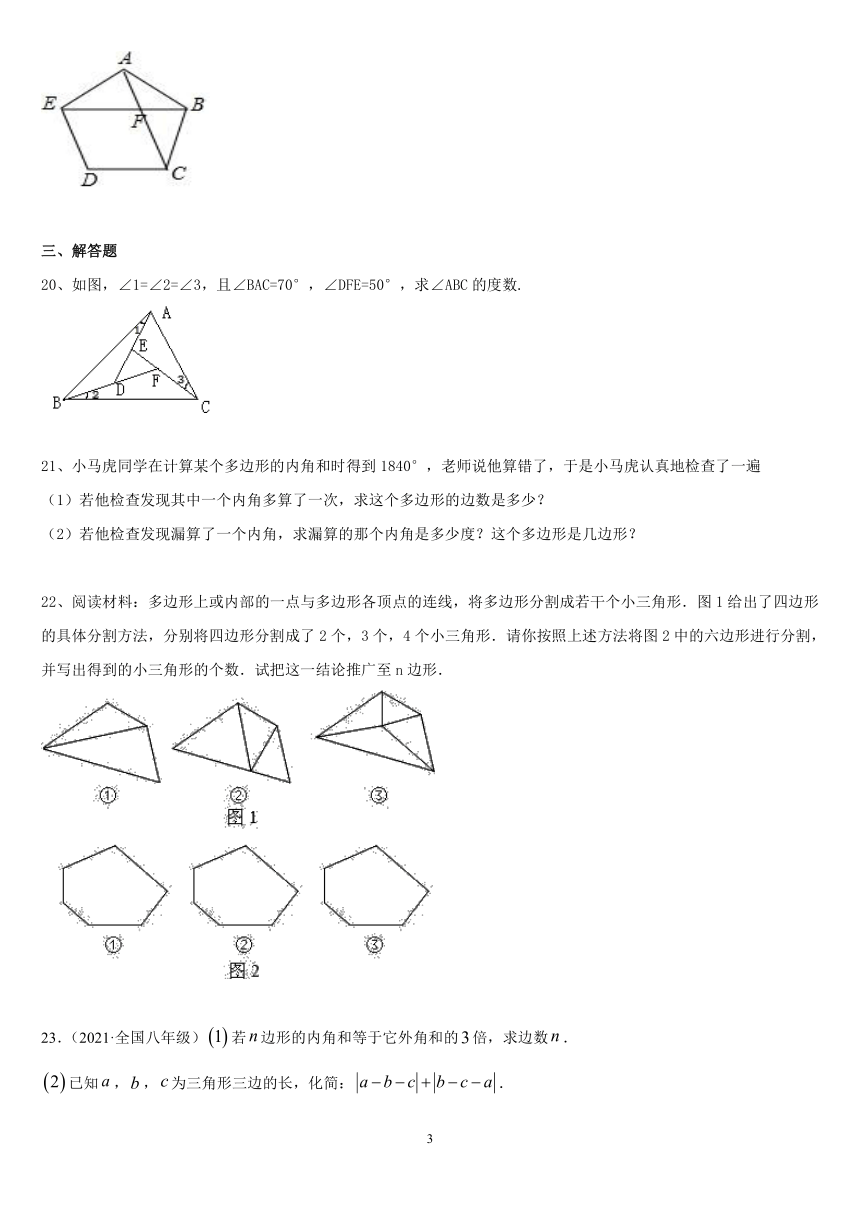
19.如图,正五边形ABCDE中,对角线AC与BE相交于点F,则_______度.
三、解答题
20、如图,∠1=∠2=∠3,且∠BAC=70°,∠DFE=50°,求∠ABC的度数.
21、小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
22、阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图1给出了四边形的具体分割方法,分别将四边形分割成了2个,3个,4个小三角形.请你按照上述方法将图2中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形.
23.(2021·全国八年级)若边形的内角和等于它外角和的倍,求边数.
已知,,为三角形三边的长,化简:.
24.(2020·内蒙古赤峰市·八年级期中)阅读材料
在平面中,我们把大于且小于的角称为优角.如果两个角相加等于,那么称这两个角互为组角,简称互组.
(1)若,互为组角,且,则______.
习惯上,我们把有一个内角大于的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角与钝角互为组角,试探索内角,,与钝角之间的数量关系,并至少用两种以上的方法说明理由.
参考答案
A
2.D
3.A
4.D
5.C
6.D
7.D
8.C
9.B
10.C
11.【答案】 十五
【考点】多边形内角与外角
解:多边形的外角和是360°,每个外角的度数是24°
360° 24=15
故答案:十五
【分析】任何多边形的外角和是360°,用外角和除以每个外角的度数即可得到边数.
12.【答案】 9
【考点】多边形内角与外角
解:设该正多边形的一个外角为 度,则其相邻的一个内角为 度,
∴ °,
解得: ,
∴该正多边形的一个外角为40°,
∵多边形外角和为360°,
∴该正多边形边数= ,
故答案为:9.
【分析】设该正多边形的一个外角为 度,则其相邻的一个内角为 度,根据二者互补进一步列出方程,求出其外角度数,然后进一步求出边数即可.
13【答案】 90°
【考点】平行线的性质,三角形内角和定理
解:设CD和BE的夹角为∠1,
∵AB∥CD,
∴∠1=∠B=50°;
∵∠C=40°,
∴∠E=180°﹣∠B﹣∠1=90°.
故答案为:90°.
【分析】根据平行线的性质得到∠1=∠B=50°,由三角形的内角和即可得到结论.
14.144°
15、540
16、3 120
17、540°或360°或180°
18.13 19.72.
20、70°
21、(1)12 (2) 140° 13
22、第一种分割法,分割成的三角形的个数比边数少2,
第二种分割法分割成的三角形的个数比边数少1,
第三种分割法分割成的三角形的个数等于多边形的边数.
23.8;.
【详解】
解:由题意得:,
解得:.
∵,,为三角形三边的长,
∴,,
∴.
24.(1)225°;(2)钝角∠BCD=∠A+∠B+∠D,理由见解析.
【详解】
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360° ,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
学习-----好资料
学习-----好资料
更多精品文档
更多精品文档
一、单选题
1.一个n边形的每个外角都是45°,则这个n边形的内角和是( )
A.1080° B.540° C.2700° D.2160°
2.一个多边形的外角和等于360°,则这个多边形的边数为( )
A.3 B.4
C.5 D.以上均有可能
3.如果一个多边形的外角和等于其内角和的2倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.如图,∠BDC=100°,∠C=35°,∠A=28°,则∠B的度数是( )
A.43° B.33° C.47° D.37°
5.如果一个多边形的内角和为,那么从这个多边形的一个顶点可以作( )条对角线.
A. B. C. D.
6.如图,在四边形中,,分别是两组对边延长线的交点,,分别是,的角平分线.若,,则( )
A. B. C. D.
7把一个正方形截去一个角后得到的多边形是
A. 三角形 B. 四边形 C. 五边形 D. 以上都有可能
8八边形一共有条对角线.
A. B. C. D.
9若一个多边形的内角和为,则从该多边形的一个顶点出发的对角线条数是
A. B. C. D.
10.(2020·江苏无锡市·七年级期中)图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
二、填空题
11.已知一个多边形的每个外角都是24°,此多边形是________边形.
12若一个正多边形的内角是外角的3倍还多20°,则这个多边形的边数是________.
13.如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于________.
14.(2021·陕西西安市·西北工业大学附属中学九年级一模)从正多边形一个顶点最多可以作7条对角线,这个正多边形每个内角的大小是_____.
15、通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是 度.
16、一个多边形的一个外角为α,且该多边形的内角和与α的和等于840°,则这个多边形的边数为 ,α= 度.
17、如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .
18.(2020·成都市金牛实验中学校七年级月考)如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
19.如图,正五边形ABCDE中,对角线AC与BE相交于点F,则_______度.
三、解答题
20、如图,∠1=∠2=∠3,且∠BAC=70°,∠DFE=50°,求∠ABC的度数.
21、小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
22、阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图1给出了四边形的具体分割方法,分别将四边形分割成了2个,3个,4个小三角形.请你按照上述方法将图2中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形.
23.(2021·全国八年级)若边形的内角和等于它外角和的倍,求边数.
已知,,为三角形三边的长,化简:.
24.(2020·内蒙古赤峰市·八年级期中)阅读材料
在平面中,我们把大于且小于的角称为优角.如果两个角相加等于,那么称这两个角互为组角,简称互组.
(1)若,互为组角,且,则______.
习惯上,我们把有一个内角大于的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角与钝角互为组角,试探索内角,,与钝角之间的数量关系,并至少用两种以上的方法说明理由.
参考答案
A
2.D
3.A
4.D
5.C
6.D
7.D
8.C
9.B
10.C
11.【答案】 十五
【考点】多边形内角与外角
解:多边形的外角和是360°,每个外角的度数是24°
360° 24=15
故答案:十五
【分析】任何多边形的外角和是360°,用外角和除以每个外角的度数即可得到边数.
12.【答案】 9
【考点】多边形内角与外角
解:设该正多边形的一个外角为 度,则其相邻的一个内角为 度,
∴ °,
解得: ,
∴该正多边形的一个外角为40°,
∵多边形外角和为360°,
∴该正多边形边数= ,
故答案为:9.
【分析】设该正多边形的一个外角为 度,则其相邻的一个内角为 度,根据二者互补进一步列出方程,求出其外角度数,然后进一步求出边数即可.
13【答案】 90°
【考点】平行线的性质,三角形内角和定理
解:设CD和BE的夹角为∠1,
∵AB∥CD,
∴∠1=∠B=50°;
∵∠C=40°,
∴∠E=180°﹣∠B﹣∠1=90°.
故答案为:90°.
【分析】根据平行线的性质得到∠1=∠B=50°,由三角形的内角和即可得到结论.
14.144°
15、540
16、3 120
17、540°或360°或180°
18.13 19.72.
20、70°
21、(1)12 (2) 140° 13
22、第一种分割法,分割成的三角形的个数比边数少2,
第二种分割法分割成的三角形的个数比边数少1,
第三种分割法分割成的三角形的个数等于多边形的边数.
23.8;.
【详解】
解:由题意得:,
解得:.
∵,,为三角形三边的长,
∴,,
∴.
24.(1)225°;(2)钝角∠BCD=∠A+∠B+∠D,理由见解析.
【详解】
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360° ,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
学习-----好资料
学习-----好资料
更多精品文档
更多精品文档
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
