三角形全等的判定课件
图片预览


文档简介
课件29张PPT。三角形全等的判定
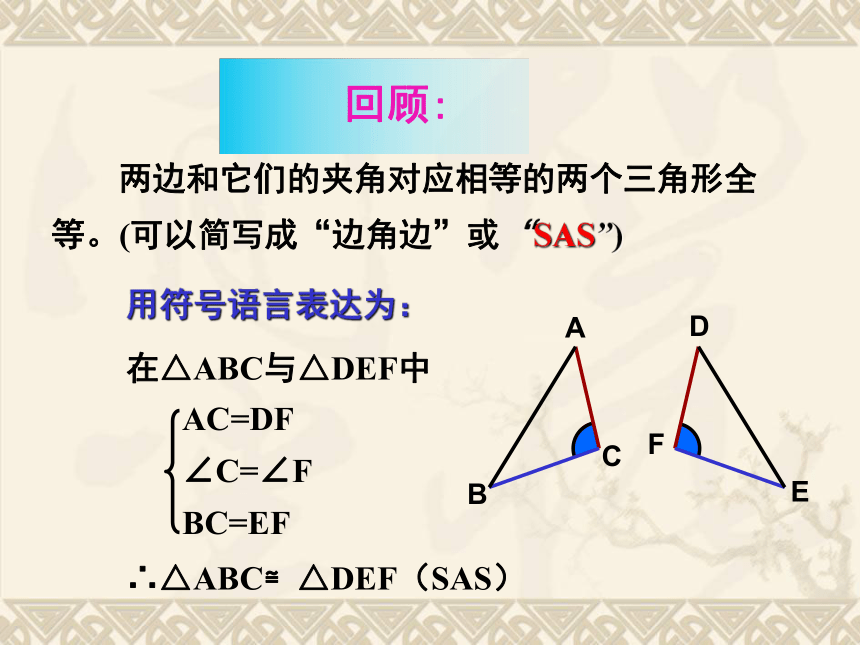
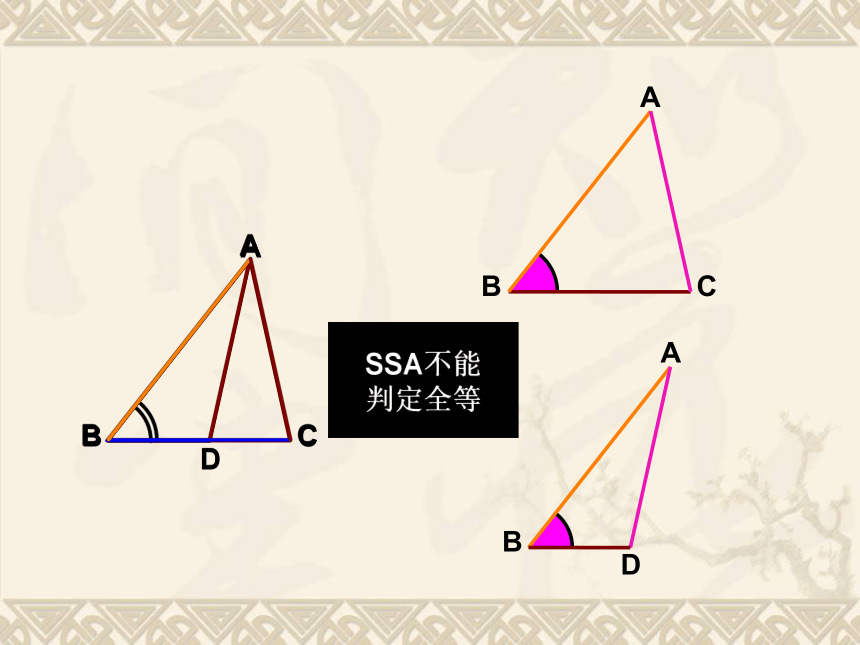
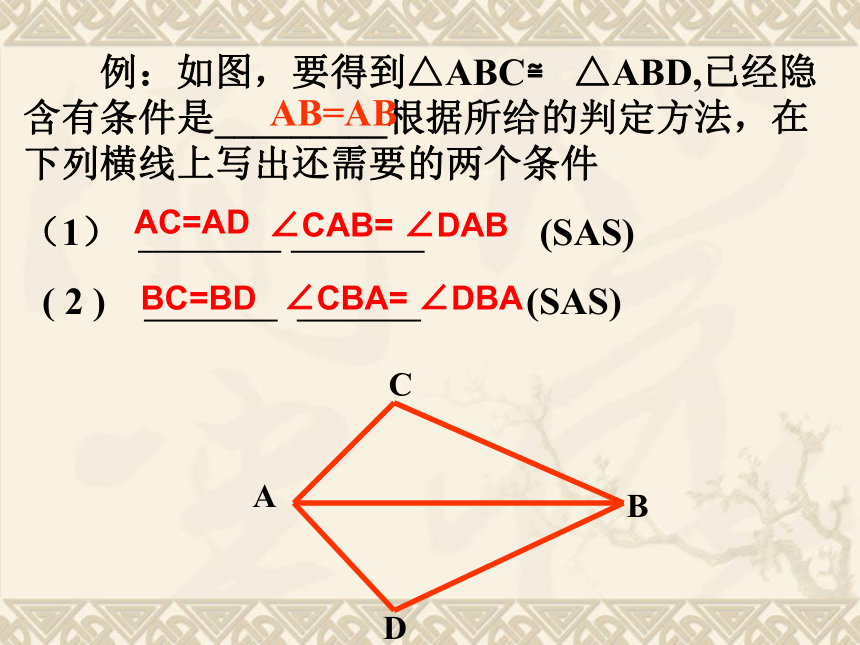
ASA或AAS用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBAABDABCSSA不能判定全等 例:如图,要得到△ABC≌ △ABD,已经隐含有条件是_________根据所给的判定方法,在下列横线上写出还需要的两个条件
(1) (SAS)
( 2 ) (SAS)AB=ABAC=AD∠CAB= ∠DABBC=BD∠CBA= ∠DBA两个三角形的全等,
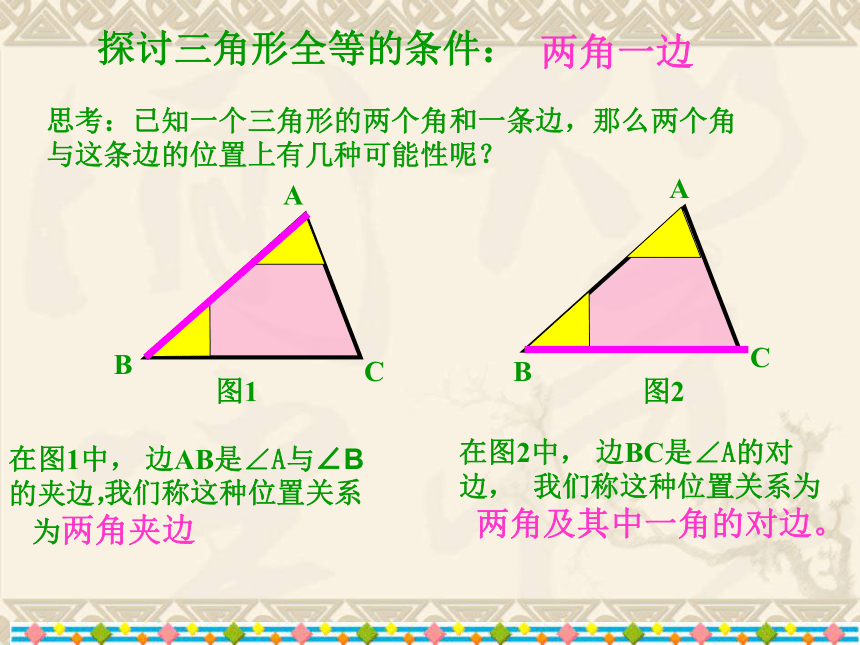
我们进行了哪些探索?③三个条件②两个条件①一个条件一边一角两角一边一角三角两边两角一边?(两边夹角) 探讨三角形全等的条件:两角一边思考:已知一个三角形的两个角和一条边,那么两个角
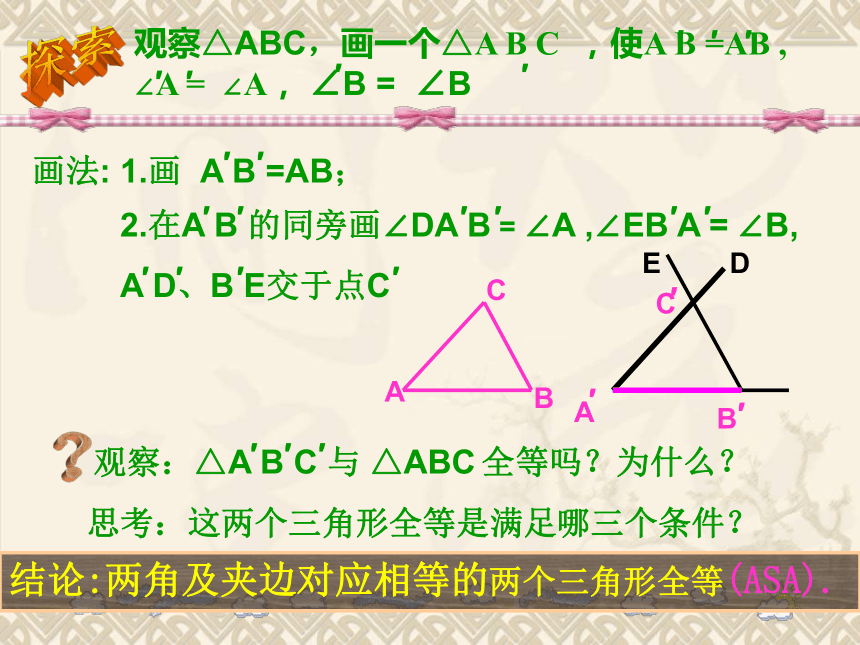
与这条边的位置上有几种可能性呢?ABCABC图1图2在图1中, 边AB是∠A与∠B的夹边,在图2中, 边BC是∠A的对边, 我们称这种位置关系为两角夹边 我们称这种位置关系为两角及其中一角的对边。观察△ABC,画一个△A B C ,使A B =AB , ∠A = ∠A, ∠B = ∠B结论:两角及夹边对应相等的两个三角形全等(ASA).′′′′′′′探索?观察:△A B C 与 △ABC 全等吗?为什么?画法: 1.画 A B =AB;2.在A B 的同旁画∠DA B = ∠A ,∠EB A = ∠B,
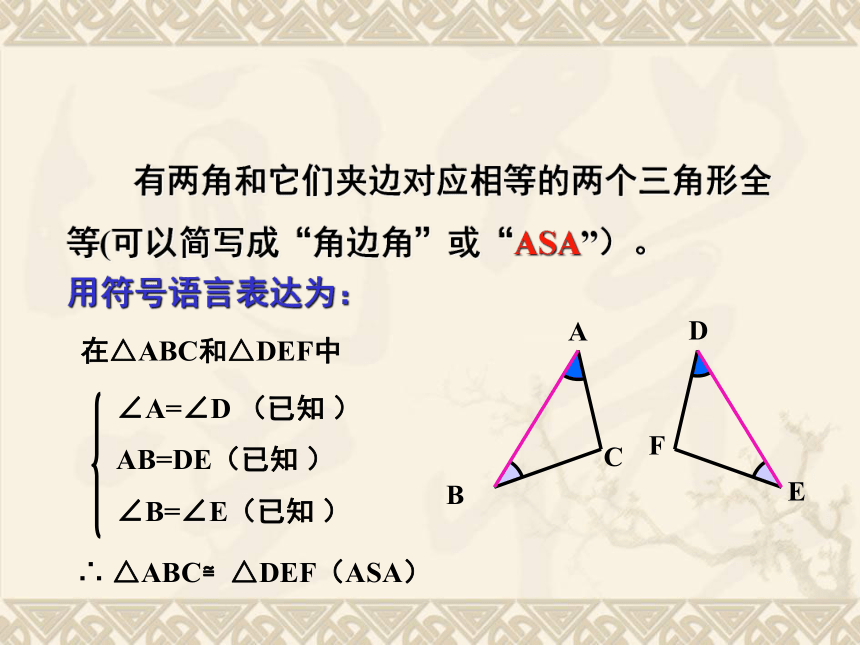
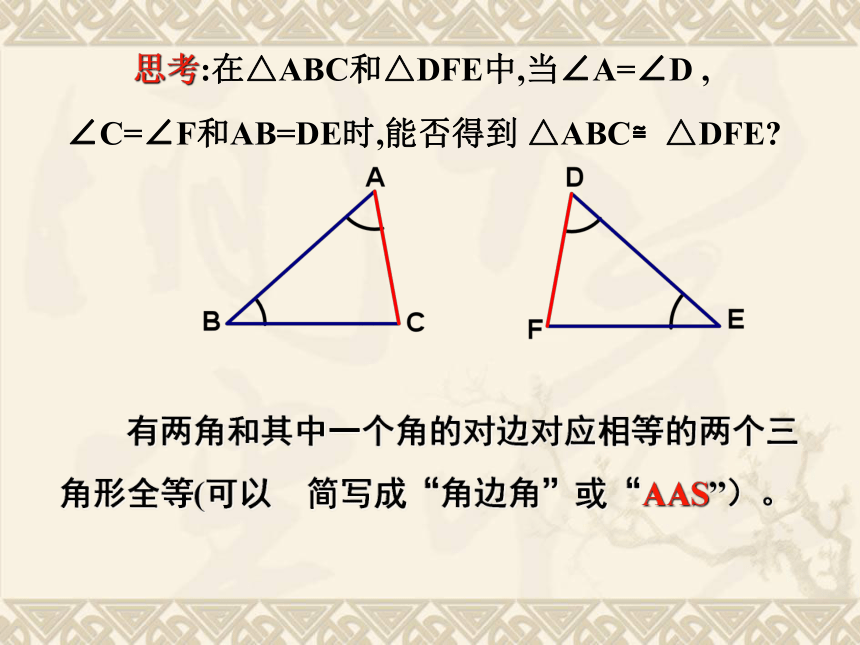
A D、B E交于点C′′′′′′′′′A′EDCB′′′思考:这两个三角形全等是满足哪三个条件?′′′′′在△ABC和△DEF中∴ △ABC≌△DEF(ASA) 有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。用符号语言表达为:FEDCBA 思考:在△ABC和△DFE中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE? 有两角和其中一个角的对边对应相等的两个三角形全等(可以 简写成“角边角”或“AAS”)。1.两个直角三角形中,斜边和一锐角对应相等,这两个
直角三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相
等,这两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS 例1:如图,点D在AB上,点E在AC上,AB=AC, ∠B= ∠C,求证:AD=AE ∠B=∠C(已知) 证明:在△ABE和△ACD中AB=AC(已知)∠A=∠A(公共角)∴△ABE≌△ACD(ASA)∴AD=AE(全等三角形的对应边相等)例2:如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF。证明:∵ BE=CF(已知) ∴BC=EF(等式性质) ∠B=∠E 在△ABC和△DEF中BC=EF ∠C=∠F∴△ABC≌△DEF(ASA) 例3:已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:例4:如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD234证明:∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2
∠3=∠4 (两直线平行,内错角相等)
∴在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA)
∴ AB=CD BC=AD(全等三角形对应边相等)1例5:如图,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明在△ABC和△DCB中,∵
∴ △ABC≌△DCB( )A.S.A.AAS?例6:如图,已知AB=AC,∠ADB= ∠AEC,
求证:△ABD≌△ACE证明:∵ AB=AC,
∴ ∠B= ∠C(等边对等角)
∵ ∠ADB= ∠AEC, AB=AC,
∴ △ABD≌△ACE(AAS)ABCDEF 如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ------------------------- ,才能使△ABC≌△DEF (写出一个即可)。∠B=∠E或∠A=∠D或 AC=DF你能吗(ASA)(AAS)(SAS)利用“角边角定理”可知,带B块去,可以配到一个与原来全等的三角形玻璃。如图,小明不慎将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃?如果可以,带哪块去合适?说明理由。玻璃问题若△ABC中, BE⊥AD于E, CF⊥AD于F,且BE=CF,那么BD与CD相等吗?为什么?证明:∵ BE⊥AD, CF⊥AD(已知)∴∠BED=∠CFD= (垂直的定义) 在△BDE和△CDF中∠BED=∠CFD(已证)∠BDE=∠CDF(对顶角相等)BE=CF(已知)∴△BDE≌△CDF(AAS)更上一层楼ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。
∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC ∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中即∠BAC=∠DAE ???í=(已知)ADAB更上一层楼练一练1.已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′,
则△ABC≌△ A′B′C′的根据是( )
A; SAS B: ASA C: AAS D:都不对
BD2.已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
3.如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。∠AEC=∠BFDAC=BD∠A=∠B∠C=∠DAC=BD∠A=∠B 4.如图,O是AB的中点, = , 与 全等吗?
为什么?两角和夹边对应相等(已知)(中点的定义)(对顶角相等)在 和 中( ) 5、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。
因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,所以不全等。 7. 如图,△ABC是等腰三角形,AD、 BE分别是
∠BAC、∠ABC的角平分线,△ABD和△BAE全等吗?
试说明理由.
全等。
∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE
∵ AD、 BE分别是
∠BAC、∠ABC的角平分线
∴ ∠BAD=∠ABE=等腰△ABC底角的一半
∵AB=BA
∴ △ABD≌△BAE(ASA)8.已知 和 中, = ,AB=AC.求证: (1) (3) AB=AC(4) BD=CE证明: (2) AE=AD (全等三角形对应边相等)(已知)(已知)(公共角)(全等三角形对应边相等)(等式的性质)1. 已知:点E是正方形ABCD的边CD上一点,
点F是CB的延长线上一点,且EA⊥AF,
求证:DE=BF2. 如图,CD⊥AB于D,BE⊥AC与E,BE、CD交于O,且AO平分∠BAC,求证:OB=OC作业:3.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A, C,E在一条直线上,这时测得DE的长就是AB的长。为什么?4、如图,已知∠1=∠2 ∠3=∠4
求证:BD=CD小结(1) 两角和它们的夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.(2) 两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.(3)三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
ASA或AAS用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBAABDABCSSA不能判定全等 例:如图,要得到△ABC≌ △ABD,已经隐含有条件是_________根据所给的判定方法,在下列横线上写出还需要的两个条件
(1) (SAS)
( 2 ) (SAS)AB=ABAC=AD∠CAB= ∠DABBC=BD∠CBA= ∠DBA两个三角形的全等,
我们进行了哪些探索?③三个条件②两个条件①一个条件一边一角两角一边一角三角两边两角一边?(两边夹角) 探讨三角形全等的条件:两角一边思考:已知一个三角形的两个角和一条边,那么两个角
与这条边的位置上有几种可能性呢?ABCABC图1图2在图1中, 边AB是∠A与∠B的夹边,在图2中, 边BC是∠A的对边, 我们称这种位置关系为两角夹边 我们称这种位置关系为两角及其中一角的对边。观察△ABC,画一个△A B C ,使A B =AB , ∠A = ∠A, ∠B = ∠B结论:两角及夹边对应相等的两个三角形全等(ASA).′′′′′′′探索?观察:△A B C 与 △ABC 全等吗?为什么?画法: 1.画 A B =AB;2.在A B 的同旁画∠DA B = ∠A ,∠EB A = ∠B,
A D、B E交于点C′′′′′′′′′A′EDCB′′′思考:这两个三角形全等是满足哪三个条件?′′′′′在△ABC和△DEF中∴ △ABC≌△DEF(ASA) 有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。用符号语言表达为:FEDCBA 思考:在△ABC和△DFE中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE? 有两角和其中一个角的对边对应相等的两个三角形全等(可以 简写成“角边角”或“AAS”)。1.两个直角三角形中,斜边和一锐角对应相等,这两个
直角三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相
等,这两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS 例1:如图,点D在AB上,点E在AC上,AB=AC, ∠B= ∠C,求证:AD=AE ∠B=∠C(已知) 证明:在△ABE和△ACD中AB=AC(已知)∠A=∠A(公共角)∴△ABE≌△ACD(ASA)∴AD=AE(全等三角形的对应边相等)例2:如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF。证明:∵ BE=CF(已知) ∴BC=EF(等式性质) ∠B=∠E 在△ABC和△DEF中BC=EF ∠C=∠F∴△ABC≌△DEF(ASA) 例3:已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:例4:如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD234证明:∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2
∠3=∠4 (两直线平行,内错角相等)
∴在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA)
∴ AB=CD BC=AD(全等三角形对应边相等)1例5:如图,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明在△ABC和△DCB中,∵
∴ △ABC≌△DCB( )A.S.A.AAS?例6:如图,已知AB=AC,∠ADB= ∠AEC,
求证:△ABD≌△ACE证明:∵ AB=AC,
∴ ∠B= ∠C(等边对等角)
∵ ∠ADB= ∠AEC, AB=AC,
∴ △ABD≌△ACE(AAS)ABCDEF 如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ------------------------- ,才能使△ABC≌△DEF (写出一个即可)。∠B=∠E或∠A=∠D或 AC=DF你能吗(ASA)(AAS)(SAS)利用“角边角定理”可知,带B块去,可以配到一个与原来全等的三角形玻璃。如图,小明不慎将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃?如果可以,带哪块去合适?说明理由。玻璃问题若△ABC中, BE⊥AD于E, CF⊥AD于F,且BE=CF,那么BD与CD相等吗?为什么?证明:∵ BE⊥AD, CF⊥AD(已知)∴∠BED=∠CFD= (垂直的定义) 在△BDE和△CDF中∠BED=∠CFD(已证)∠BDE=∠CDF(对顶角相等)BE=CF(已知)∴△BDE≌△CDF(AAS)更上一层楼ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。
∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC ∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中即∠BAC=∠DAE ???í=(已知)ADAB更上一层楼练一练1.已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′,
则△ABC≌△ A′B′C′的根据是( )
A; SAS B: ASA C: AAS D:都不对
BD2.已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
3.如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。∠AEC=∠BFDAC=BD∠A=∠B∠C=∠DAC=BD∠A=∠B 4.如图,O是AB的中点, = , 与 全等吗?
为什么?两角和夹边对应相等(已知)(中点的定义)(对顶角相等)在 和 中( ) 5、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。
因为虽然有两组内角相等,且BC=BC,但不都是两个三角形两组内角的夹边,所以不全等。 7. 如图,△ABC是等腰三角形,AD、 BE分别是
∠BAC、∠ABC的角平分线,△ABD和△BAE全等吗?
试说明理由.
全等。
∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE
∵ AD、 BE分别是
∠BAC、∠ABC的角平分线
∴ ∠BAD=∠ABE=等腰△ABC底角的一半
∵AB=BA
∴ △ABD≌△BAE(ASA)8.已知 和 中, = ,AB=AC.求证: (1) (3) AB=AC(4) BD=CE证明: (2) AE=AD (全等三角形对应边相等)(已知)(已知)(公共角)(全等三角形对应边相等)(等式的性质)1. 已知:点E是正方形ABCD的边CD上一点,
点F是CB的延长线上一点,且EA⊥AF,
求证:DE=BF2. 如图,CD⊥AB于D,BE⊥AC与E,BE、CD交于O,且AO平分∠BAC,求证:OB=OC作业:3.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A, C,E在一条直线上,这时测得DE的长就是AB的长。为什么?4、如图,已知∠1=∠2 ∠3=∠4
求证:BD=CD小结(1) 两角和它们的夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.(2) 两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.(3)三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
