2021-2022学年鲁教版六年级数学下册《6-7完全平方公式》同步练习题(Word版 附答案)
文档属性
| 名称 | 2021-2022学年鲁教版六年级数学下册《6-7完全平方公式》同步练习题(Word版 附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 58.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 22:18:58 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学下册《6-7完全平方公式》同步练习题(附答案)
1.若关于x的二次三项式x2﹣ax+36是一个完全平方式,那么a的值是( )
A.12 B.±12 C.6 D.±6
2.已知xy=﹣3,x+y=﹣4,则x2+3xy+y2值为( )
A.1 B.7 C.13 D.31
3.若a2+ab+b2+A=(a﹣b)2,那么A等于( )
A.﹣3ab B.﹣ab C.0 D.ab
4.(a﹣b+c)(﹣a+b﹣c)等于( )
A.﹣(a﹣b+c)2 B.c2﹣(a﹣b)2 C.(a﹣b)2﹣c2 D.c2﹣a+b2
5.已知a+b=3,ab=,则a2+b2的值等于( )
A.6 B.7 C.8 D.9
6.已知x﹣y=4,xy=2,那么(x+y)2的值为( )
A.24 B.20 C.12 D.8
7.若n满足(n﹣2021)2+(2022﹣n)2=1,则(n﹣2021)(2022﹣n)的值为( )
A.﹣1 B.0 C. D.1
8.已知(m﹣53)(m﹣47)=25,则(m﹣53)2+(m﹣47)2的值为( )
A.136 B.86 C.36 D.50
9.对于代数式x2﹣2(k﹣1)x+2k+6,甲同学认为:当x=1时,该代数式的值与k无关;乙同学认为:当该代数式是一个完全平方式时,k只能为5.则下列结论正确的是( )
A.只有甲正确 B.只有乙正确 C.甲乙都正确 D.甲乙都错误
10.如果(a+b)2=16,(a﹣b)2=4,且a、b是长方形的长和宽,则这个长方形的面积是( )
A.3 B.4 C.5 D.6
11.如图中,利用面积的等量关系验证的公式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+2b)(a﹣b)=a2+ab﹣2b2 D.(a+b)2=a2+2ab+b2
12.已知多项式x2+4与一个单项式的和是一个多项式的平方,则下列选项中的单项式不满足条件的是( )
A.4x B.﹣4x C.x4 D.x4
13.如果x2+(m﹣1)x+9是一个完全平方式,那么m的值是( )
A.7 B.﹣7 C.﹣5或7 D.﹣5或5
14.计算:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2].
15.已知:|3﹣xy|+(x+y﹣2)2=0,求x2+y2+4xy的值.
16.若x、y满足x2+y2=5,xy=﹣1,求下列各式的值.
(1)(x+y)2.
(2)x4+y4.
17.阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路回答下列问题:
(1)已知a+b=5,ab=7,求,a2﹣ab+b2的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
18.阅读下列解答过程:
已知:x≠0,且满足x2﹣3x=1.求:的值.
解:∵x2﹣3x=1,∴x2﹣3x﹣1=0
∴,即.
∴==32+2=11.
请通过阅读以上内容,解答下列问题:
已知a≠0,且满足(2a+1)(1﹣2a)﹣(3﹣2a)2+9a2=14a﹣7,
求:(1)的值;(2)的值.
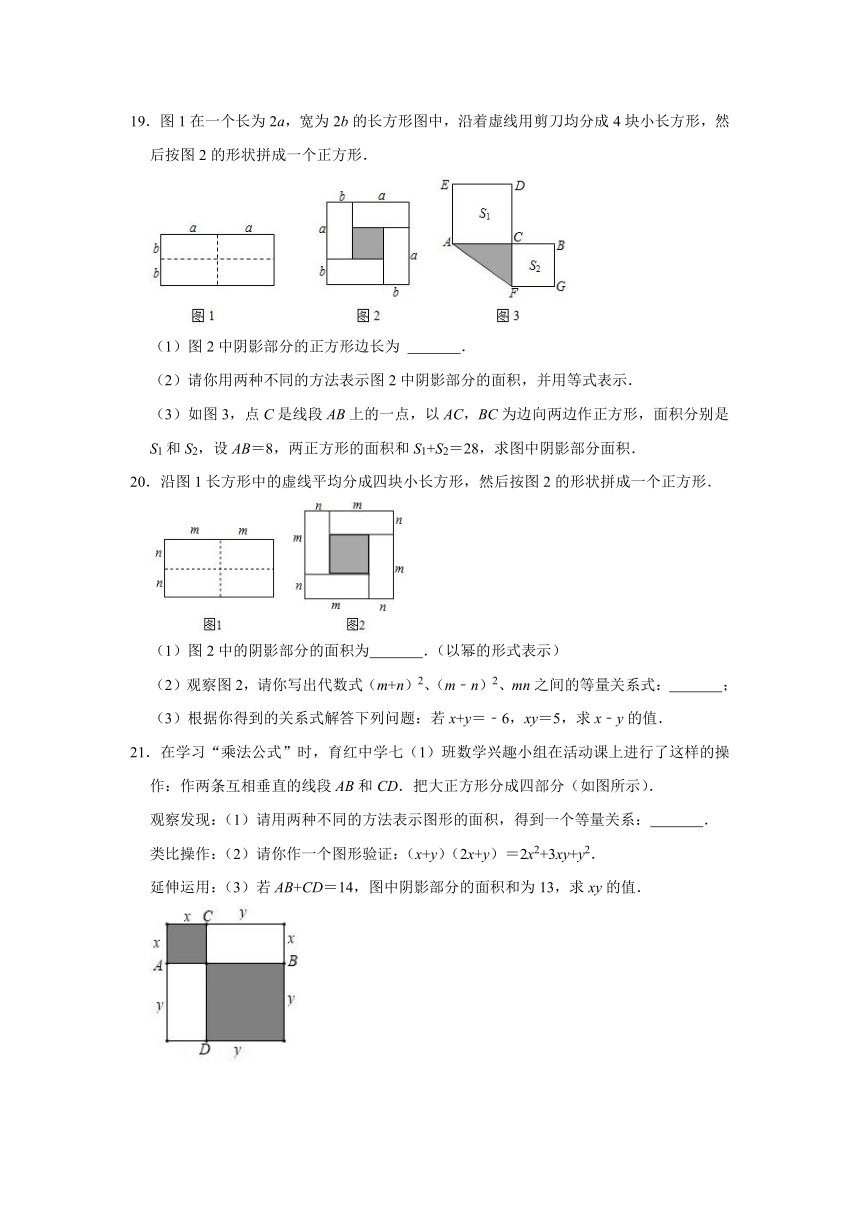
19.图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=28,求图中阴影部分面积.
20.沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中的阴影部分的面积为 .(以幂的形式表示)
(2)观察图2,请你写出代数式(m+n)2、(m﹣n)2、mn之间的等量关系式: ;
(3)根据你得到的关系式解答下列问题:若x+y=﹣6,xy=5,求x﹣y的值.
21.在学习“乘法公式”时,育红中学七(1)班数学兴趣小组在活动课上进行了这样的操作:作两条互相垂直的线段AB和CD.把大正方形分成四部分(如图所示).
观察发现:(1)请用两种不同的方法表示图形的面积,得到一个等量关系: .
类比操作:(2)请你作一个图形验证:(x+y)(2x+y)=2x2+3xy+y2.
延伸运用:(3)若AB+CD=14,图中阴影部分的面积和为13,求xy的值.
参考答案
1.解:∵x2﹣ax+36是一个完全平方式,
∴a=±12,
故选:B.
2.解:∵xy=﹣3,x+y=﹣4,
∴x2+3xy+y2
=(x+y)2+xy
=(﹣4)2+(﹣3)
=13,
故选:C.
3.解:∵(a﹣b)2=a2﹣2ab+b2
又∵a2+ab+b2+A=(a﹣b)2,
∴A=a2﹣2ab+b2﹣(a2+ab+b2)=﹣3ab.
故选:A.
4.解:(a﹣b+c)(﹣a+b﹣c)=﹣(a﹣b+c)2.
故选:A.
5.解:∵a+b=3,
∴(a+b)2=32=9,
∴a2+b2=(a+b)2﹣2ab=9﹣3=6.
故选:A.
6.解:设n﹣2021=x,2022﹣n=y,
∴x+y
=n﹣2021+2022﹣n
=1,
∵(n﹣2021)2+(2022﹣n)2=1,
∴x2+y2=1,
∵x+y=1,
∴(x+y)2=1,
∴x2+2xy+y2=1,
∴xy=0,
∴(n﹣2021)(2022﹣n)=0,
故选:B.
7.解:设a=m﹣53,b=m﹣47,则ab=25,a﹣b=﹣6,
∴a2+b2=(a﹣b)2+2ab=(﹣6)2+50=86,
∴(m﹣53)2+(m﹣47)2=86,
故选:B.
8.解:(1)当x=1时,该代数式=1﹣2(k﹣1)+2k+6=9,
∴当x=1时,该代数式的值与k无关,故甲同学的结论正确;
当代数式x2﹣2(k﹣1)x+2k+6是一个完全平方式时,
(k﹣1)2=2k+6,
k2﹣2k+1=2k+6,
k2﹣4k﹣5=0,
(k﹣5)(k+1)=0,
k=5或k=﹣1,
当k=5时,原式=x2﹣8x+16=(x﹣4)2,
当k=﹣1时,原式=x2+4x+4=(x+2)2,
∴k=5或k=﹣1均符合题意,
故乙同学的结论错误.
故选:A.
9.解:(x+y)2=(x﹣y)2+4xy,
因为x﹣y=4,xy=2,
所以(x+y)2=42+4×2=24.
故选:A.
10.解:∵(a+b)2=16,(a﹣b)2=4,
∴(a+b)2﹣(a﹣b)2=4ab=12,
∴ab=3,
∴长方形的面积为3,
故选:A.
11.解:图中正方形的面积可表示为:a2+2ab+b2,
也可表示为:(a+b)2,
故a2+2ab+b2=(a+b)2.
故选:D.
12.解:∵(x±2)2=x2±4x+4,
+x2+4=,
∴多项式x2+4与4x或﹣4x或的和是一个整式的完全平方式.
多项式x2+4与的和不是一个多项式的平方,
故选:D.
13.解:∵x2+(m﹣1)x+9是一个完全平方式,
∴(m﹣1)x=±2 x 3,
∴m﹣1=±6,
∴m=﹣5或7,
故选:C.
14.解:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2]
=(2a+b)2(a2﹣2ab+b2+2a2﹣2ab+a2)
=(2a+b)2(4a2﹣4ab+b2)
=(2a+b)2(2a﹣b)2
=(4a2﹣b2)2
=16a4﹣8a2b2+b4.
15.解:∵|3﹣xy|+(x+y﹣2)2=0,
∴3﹣xy=0,x+y﹣2=0,
∴xy=3,x+y=2,
∴x2+y2+4xy=(x+y)2+2xy=22+2×3=10.
16.解:(1)原式=x2+y2+2xy,
当x2+y2=5,xy=﹣1时,原式=5+2×(﹣1)=3;
(2)原式=(x2+y2)2﹣2x2y2
=(x2+y2)2﹣2(xy)2,
当x2+y2=5,xy=﹣1时,原式=52﹣2×(﹣1)2=23.
17.解:(1)∵a+b=5,ab=7,
∴===,
a2﹣ab+b2=(a+b)2﹣2ab﹣ab=(a+b)2﹣3ab=52﹣3×7=4.
(2)(a﹣b)2+c2=[(a﹣b)﹣c]2+2(a﹣b)c
=(a﹣c﹣b)2+2(a﹣b)c
=(﹣10)2+2×(﹣12)
=76.
18.解:(1)(2a+1)(1﹣2a)﹣(3﹣2a)2+9a2=14a﹣71﹣4a2﹣(9﹣12a+4a2)+9a2﹣14a+7=0,
整理得:a2﹣2a﹣1=0
∴,
∴;
(2)解:的倒数为,
∵,
∴.
19.解:(1)由大、小正方形的边长与长方形边长之间的关系可得,
阴影部分是边长为(a﹣b)的正方形,
故答案为:a﹣b;
(2)方法一:阴影部分是边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
方法2:从边长为(a+b)的正方形面积减去4个长为a,宽为b长方形的面积可得,
(a+b)2﹣4ab,
于是有:(a﹣b)2=(a+b)2﹣4ab;
(3)设大正方形的边长为a、小正方形的边长b,
则a+b=8,a2+b2=28,
由(a+b)2=a2+b2+2ab得,
82=28+2ab,
即ab=18,
因此阴影部分的面积为ab=9,
答:阴影部分的面积为9.
20.解:(1)图2中的阴影部分的边长为m﹣n,
∴其面积为(m﹣n)2;
故答案为:(m﹣n)2;
(2)图2中的阴影部分的面积也可以为(m+n)2﹣4mn,
∴代数式(m+n)2、(m﹣n)2、mn之间的等量关系式:(m+n)2﹣4mn=(m﹣n)2;
故答案为:(m+n)2﹣4mn=(m﹣n)2;
(3)(x﹣y)2=(x+y)2﹣4xy=36﹣20=16,
∴x﹣y=±4.
21.解:(1)由图知,大正方形的边长为x+y,则大正方形的面积为(x+y)2,
∵大正方形的面积为各部分面积和:x2+2xy+y2,
∴(x+y)2=x2+2xy+y2,
故答案为(x+y)2=x2+2xy+y2;
(2)如图所示,
(3)∵AB+CD=14,
∴x+y=7,
∵阴影部分的面积和为13,
∴x2+y2=13,
∵(x+y)2=x2+2xy+y2,
∴72=13+2xy,
∴xy=18.
1.若关于x的二次三项式x2﹣ax+36是一个完全平方式,那么a的值是( )
A.12 B.±12 C.6 D.±6
2.已知xy=﹣3,x+y=﹣4,则x2+3xy+y2值为( )
A.1 B.7 C.13 D.31
3.若a2+ab+b2+A=(a﹣b)2,那么A等于( )
A.﹣3ab B.﹣ab C.0 D.ab
4.(a﹣b+c)(﹣a+b﹣c)等于( )
A.﹣(a﹣b+c)2 B.c2﹣(a﹣b)2 C.(a﹣b)2﹣c2 D.c2﹣a+b2
5.已知a+b=3,ab=,则a2+b2的值等于( )
A.6 B.7 C.8 D.9
6.已知x﹣y=4,xy=2,那么(x+y)2的值为( )
A.24 B.20 C.12 D.8
7.若n满足(n﹣2021)2+(2022﹣n)2=1,则(n﹣2021)(2022﹣n)的值为( )
A.﹣1 B.0 C. D.1
8.已知(m﹣53)(m﹣47)=25,则(m﹣53)2+(m﹣47)2的值为( )
A.136 B.86 C.36 D.50
9.对于代数式x2﹣2(k﹣1)x+2k+6,甲同学认为:当x=1时,该代数式的值与k无关;乙同学认为:当该代数式是一个完全平方式时,k只能为5.则下列结论正确的是( )
A.只有甲正确 B.只有乙正确 C.甲乙都正确 D.甲乙都错误
10.如果(a+b)2=16,(a﹣b)2=4,且a、b是长方形的长和宽,则这个长方形的面积是( )
A.3 B.4 C.5 D.6
11.如图中,利用面积的等量关系验证的公式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+2b)(a﹣b)=a2+ab﹣2b2 D.(a+b)2=a2+2ab+b2
12.已知多项式x2+4与一个单项式的和是一个多项式的平方,则下列选项中的单项式不满足条件的是( )
A.4x B.﹣4x C.x4 D.x4
13.如果x2+(m﹣1)x+9是一个完全平方式,那么m的值是( )
A.7 B.﹣7 C.﹣5或7 D.﹣5或5
14.计算:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2].
15.已知:|3﹣xy|+(x+y﹣2)2=0,求x2+y2+4xy的值.
16.若x、y满足x2+y2=5,xy=﹣1,求下列各式的值.
(1)(x+y)2.
(2)x4+y4.
17.阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路回答下列问题:
(1)已知a+b=5,ab=7,求,a2﹣ab+b2的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
18.阅读下列解答过程:
已知:x≠0,且满足x2﹣3x=1.求:的值.
解:∵x2﹣3x=1,∴x2﹣3x﹣1=0
∴,即.
∴==32+2=11.
请通过阅读以上内容,解答下列问题:
已知a≠0,且满足(2a+1)(1﹣2a)﹣(3﹣2a)2+9a2=14a﹣7,
求:(1)的值;(2)的值.
19.图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=28,求图中阴影部分面积.
20.沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中的阴影部分的面积为 .(以幂的形式表示)
(2)观察图2,请你写出代数式(m+n)2、(m﹣n)2、mn之间的等量关系式: ;
(3)根据你得到的关系式解答下列问题:若x+y=﹣6,xy=5,求x﹣y的值.
21.在学习“乘法公式”时,育红中学七(1)班数学兴趣小组在活动课上进行了这样的操作:作两条互相垂直的线段AB和CD.把大正方形分成四部分(如图所示).
观察发现:(1)请用两种不同的方法表示图形的面积,得到一个等量关系: .
类比操作:(2)请你作一个图形验证:(x+y)(2x+y)=2x2+3xy+y2.
延伸运用:(3)若AB+CD=14,图中阴影部分的面积和为13,求xy的值.
参考答案
1.解:∵x2﹣ax+36是一个完全平方式,
∴a=±12,
故选:B.
2.解:∵xy=﹣3,x+y=﹣4,
∴x2+3xy+y2
=(x+y)2+xy
=(﹣4)2+(﹣3)
=13,
故选:C.
3.解:∵(a﹣b)2=a2﹣2ab+b2
又∵a2+ab+b2+A=(a﹣b)2,
∴A=a2﹣2ab+b2﹣(a2+ab+b2)=﹣3ab.
故选:A.
4.解:(a﹣b+c)(﹣a+b﹣c)=﹣(a﹣b+c)2.
故选:A.
5.解:∵a+b=3,
∴(a+b)2=32=9,
∴a2+b2=(a+b)2﹣2ab=9﹣3=6.
故选:A.
6.解:设n﹣2021=x,2022﹣n=y,
∴x+y
=n﹣2021+2022﹣n
=1,
∵(n﹣2021)2+(2022﹣n)2=1,
∴x2+y2=1,
∵x+y=1,
∴(x+y)2=1,
∴x2+2xy+y2=1,
∴xy=0,
∴(n﹣2021)(2022﹣n)=0,
故选:B.
7.解:设a=m﹣53,b=m﹣47,则ab=25,a﹣b=﹣6,
∴a2+b2=(a﹣b)2+2ab=(﹣6)2+50=86,
∴(m﹣53)2+(m﹣47)2=86,
故选:B.
8.解:(1)当x=1时,该代数式=1﹣2(k﹣1)+2k+6=9,
∴当x=1时,该代数式的值与k无关,故甲同学的结论正确;
当代数式x2﹣2(k﹣1)x+2k+6是一个完全平方式时,
(k﹣1)2=2k+6,
k2﹣2k+1=2k+6,
k2﹣4k﹣5=0,
(k﹣5)(k+1)=0,
k=5或k=﹣1,
当k=5时,原式=x2﹣8x+16=(x﹣4)2,
当k=﹣1时,原式=x2+4x+4=(x+2)2,
∴k=5或k=﹣1均符合题意,
故乙同学的结论错误.
故选:A.
9.解:(x+y)2=(x﹣y)2+4xy,
因为x﹣y=4,xy=2,
所以(x+y)2=42+4×2=24.
故选:A.
10.解:∵(a+b)2=16,(a﹣b)2=4,
∴(a+b)2﹣(a﹣b)2=4ab=12,
∴ab=3,
∴长方形的面积为3,
故选:A.
11.解:图中正方形的面积可表示为:a2+2ab+b2,
也可表示为:(a+b)2,
故a2+2ab+b2=(a+b)2.
故选:D.
12.解:∵(x±2)2=x2±4x+4,
+x2+4=,
∴多项式x2+4与4x或﹣4x或的和是一个整式的完全平方式.
多项式x2+4与的和不是一个多项式的平方,
故选:D.
13.解:∵x2+(m﹣1)x+9是一个完全平方式,
∴(m﹣1)x=±2 x 3,
∴m﹣1=±6,
∴m=﹣5或7,
故选:C.
14.解:(2a+b)2[(a﹣b)2+2a(a﹣b)+a2]
=(2a+b)2(a2﹣2ab+b2+2a2﹣2ab+a2)
=(2a+b)2(4a2﹣4ab+b2)
=(2a+b)2(2a﹣b)2
=(4a2﹣b2)2
=16a4﹣8a2b2+b4.
15.解:∵|3﹣xy|+(x+y﹣2)2=0,
∴3﹣xy=0,x+y﹣2=0,
∴xy=3,x+y=2,
∴x2+y2+4xy=(x+y)2+2xy=22+2×3=10.
16.解:(1)原式=x2+y2+2xy,
当x2+y2=5,xy=﹣1时,原式=5+2×(﹣1)=3;
(2)原式=(x2+y2)2﹣2x2y2
=(x2+y2)2﹣2(xy)2,
当x2+y2=5,xy=﹣1时,原式=52﹣2×(﹣1)2=23.
17.解:(1)∵a+b=5,ab=7,
∴===,
a2﹣ab+b2=(a+b)2﹣2ab﹣ab=(a+b)2﹣3ab=52﹣3×7=4.
(2)(a﹣b)2+c2=[(a﹣b)﹣c]2+2(a﹣b)c
=(a﹣c﹣b)2+2(a﹣b)c
=(﹣10)2+2×(﹣12)
=76.
18.解:(1)(2a+1)(1﹣2a)﹣(3﹣2a)2+9a2=14a﹣71﹣4a2﹣(9﹣12a+4a2)+9a2﹣14a+7=0,
整理得:a2﹣2a﹣1=0
∴,
∴;
(2)解:的倒数为,
∵,
∴.
19.解:(1)由大、小正方形的边长与长方形边长之间的关系可得,
阴影部分是边长为(a﹣b)的正方形,
故答案为:a﹣b;
(2)方法一:阴影部分是边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
方法2:从边长为(a+b)的正方形面积减去4个长为a,宽为b长方形的面积可得,
(a+b)2﹣4ab,
于是有:(a﹣b)2=(a+b)2﹣4ab;
(3)设大正方形的边长为a、小正方形的边长b,
则a+b=8,a2+b2=28,
由(a+b)2=a2+b2+2ab得,
82=28+2ab,
即ab=18,
因此阴影部分的面积为ab=9,
答:阴影部分的面积为9.
20.解:(1)图2中的阴影部分的边长为m﹣n,
∴其面积为(m﹣n)2;
故答案为:(m﹣n)2;
(2)图2中的阴影部分的面积也可以为(m+n)2﹣4mn,
∴代数式(m+n)2、(m﹣n)2、mn之间的等量关系式:(m+n)2﹣4mn=(m﹣n)2;
故答案为:(m+n)2﹣4mn=(m﹣n)2;
(3)(x﹣y)2=(x+y)2﹣4xy=36﹣20=16,
∴x﹣y=±4.
21.解:(1)由图知,大正方形的边长为x+y,则大正方形的面积为(x+y)2,
∵大正方形的面积为各部分面积和:x2+2xy+y2,
∴(x+y)2=x2+2xy+y2,
故答案为(x+y)2=x2+2xy+y2;
(2)如图所示,
(3)∵AB+CD=14,
∴x+y=7,
∵阴影部分的面积和为13,
∴x2+y2=13,
∵(x+y)2=x2+2xy+y2,
∴72=13+2xy,
∴xy=18.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
