江西省南康中学高一上学期期中考试数学试卷
文档属性
| 名称 | 江西省南康中学高一上学期期中考试数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 145.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-30 15:33:33 | ||
图片预览



文档简介
南康中学2012~2013学年度第一学期高一期中考试
数 学 试 卷
命题人:范湘霖 刘佩红 审题人:蓝建平
一、选择题(每小题5分,共50分)
1.集合的子集的个数是( )
A.64 B.8 C.6 D.3
2.设集合A、B都是正整数集,映射是把集合A中的元素n对应到集合B的元素,则在映射下象1023的原象是( )
A.11 B.10 C.9 D.8
3.为了得到函数的图像,只需把函数的图像上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向右平移3个单位长度,再向下平移1个单位长度
D.向左平移3个单位长度,再向下平移1个单位长度
4.设,则( )
A. B. C. D.
5. 设函数,现用二分法求方程在区间(1,2)内的近似解,计算得,则方程的根所在的区间是( )
A. (1,1.5) B. (1.5,1.75) C.(1,2) D. (1.75,2)
6.函数的值域是( )
A. B. C. D.
7.某林场计划第一年造林10000亩,以后每年比前一年多造林20%,则第四年造林( )亩
A.14400 B.172800 C.17280 D.20736
8.函数y=f(x)与y=g(x)的图象如所示,则函数y=f(x)·g(x)的图象可能为( )
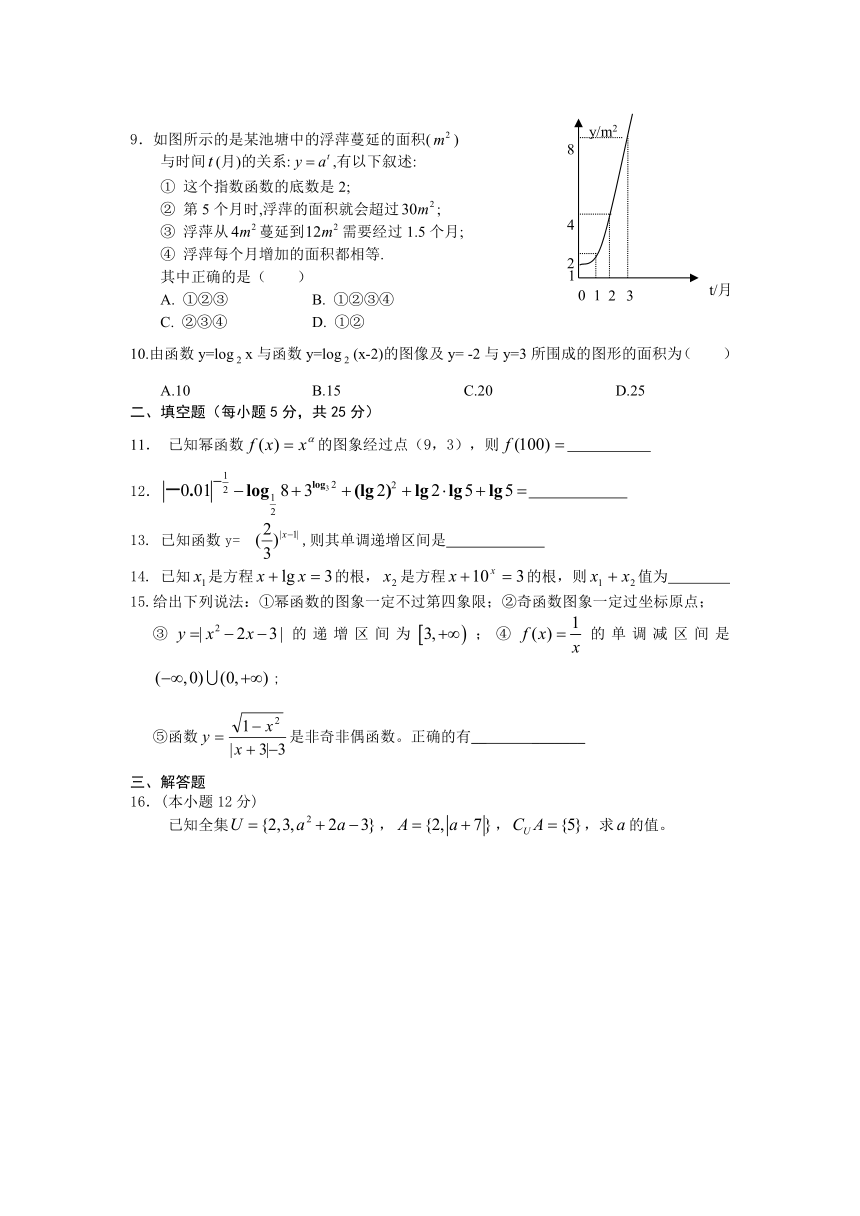
9.如图所示的是某池塘中的浮萍蔓延的面积()
与时间(月)的关系:,有以下叙述:
① 这个指数函数的底数是2;
② 第5个月时,浮萍的面积就会超过;
③ 浮萍从蔓延到需要经过1.5个月;
④ 浮萍每个月增加的面积都相等.
其中正确的是( )
A. ①②③ B. ①②③④
C. ②③④ D. ①②
10.由函数y=logx与函数y=log(x-2)的图像及y= -2与y=3所围成的图形的面积为( )
A.10 B.15 C.20 D.25
二、填空题(每小题5分,共25分)
11. 已知幂函数的图象经过点(9,3),则
12.
13. 已知函数y=,则其单调递增区间是
14. 已知是方程的根,是方程的根,则值为
15.给出下列说法:①幂函数的图象一定不过第四象限;②奇函数图象一定过坐标原点;
③的递增区间为;④的单调减区间是;
⑤函数是非奇非偶函数。正确的有__ _______
三、解答题
16.(本小题12分)
已知全集,,,求的值。
17. (本小题12分)
的定义域为,的定义域为Q,
求及.
18.(本小题12分)
已知奇函数,在时的图象是如图所示的抛物线的一部分,
(1)请补全函数的图象
(2)求函数的表达式。
19.(本小题12分)
某企业为适应市场需求,准备投入资金16万元生产R和W型两种产品。经市场预测,生产R型产品所获利润y(万元)与投入资金x(万元)满足关系y=,生产W型产品所获利润y(万元)与投入资金x(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5万元。为获得最大总利润,问生产R、W型产品各应投入资金多少万元?获得的最大总利润Q是多少?
20.(本小题13分)
设函数,
(1)若,求的取值范围;
(2)求的最值,并给出取得最值时对应的的值;
(3)讨论函数的单调性。
21. (本小题14分)
已知函数
(1)若且函数的值域为,求的表达式;
(2)在(1)的条件下, 当时, 是单调函数, 求实数k的取值范围;
(3)设, 且为偶函数, 判断+能否大于零?请说明理由。
南康中学2012~2013学年度第一学期高一期中考试
数学参考答案
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
D
C
D
A
C
A
D
A
二、填空题(每小题5分,共25分)
11、10 12、16 13、 14、3 15、①
三、解答题
16、解:据题意,有,即 ……………………2分
解得或 …………………………6分
当时, 不合题意 ………………8分
当时, 适合 ……………………10分
……………………12分
17 解:由…………4分
由 ………………8分
………………10分
………………12分
18.解:(1)
…………………………6分
(2)当时,设把代入得
………………9分
当时,由图像或利用奇函数可得 ………………11分
……………………12分
19. 解:设生产R型产品投入资金为x万元,则生产W型产品的投入资金为(16-x)万元…2分
则…………………………6分
令, 则 ………………8分
所以 ,即(万元),Q取最大值,(万元)
此时,16-x=15(万元) ………………11分
答:生产R型产品投入资金为1万元,生产W型产品的投入资金为15万元,
获得的最大总利润是万元 ……………………12分
20.解:⑴且在是增函数
………………3分
即 ……………………4分
⑵
令,则 ………………6分
函数对称轴为
当即即时, ………………7分
当即即时, ……………………8分
⑶
令,则 ………………9分
函数在上是增函数 ………………10分
函数在即在是减函数
在时,是增函数 ………………12分
原函数在上是减函数,在是增函数 ………………13分
21.解:(1) ∵,
∴ ① ……1分
又函数的值域为, 所以
且 ②
由①②得
………3分
∴.
∴ ……5分
(2) 由(1)有
, ………7分
函数的对称轴为x=
函数g(x)是上的单调函数,或,
或 ……9分
(3) ∵是偶函数 ………………10分
∴ ∴, ……11分
∵又
∴+,
∴+能大于零. ………14分
数 学 试 卷
命题人:范湘霖 刘佩红 审题人:蓝建平
一、选择题(每小题5分,共50分)
1.集合的子集的个数是( )
A.64 B.8 C.6 D.3
2.设集合A、B都是正整数集,映射是把集合A中的元素n对应到集合B的元素,则在映射下象1023的原象是( )
A.11 B.10 C.9 D.8
3.为了得到函数的图像,只需把函数的图像上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向右平移3个单位长度,再向下平移1个单位长度
D.向左平移3个单位长度,再向下平移1个单位长度
4.设,则( )
A. B. C. D.
5. 设函数,现用二分法求方程在区间(1,2)内的近似解,计算得,则方程的根所在的区间是( )
A. (1,1.5) B. (1.5,1.75) C.(1,2) D. (1.75,2)
6.函数的值域是( )
A. B. C. D.
7.某林场计划第一年造林10000亩,以后每年比前一年多造林20%,则第四年造林( )亩
A.14400 B.172800 C.17280 D.20736
8.函数y=f(x)与y=g(x)的图象如所示,则函数y=f(x)·g(x)的图象可能为( )
9.如图所示的是某池塘中的浮萍蔓延的面积()
与时间(月)的关系:,有以下叙述:
① 这个指数函数的底数是2;
② 第5个月时,浮萍的面积就会超过;
③ 浮萍从蔓延到需要经过1.5个月;
④ 浮萍每个月增加的面积都相等.
其中正确的是( )
A. ①②③ B. ①②③④
C. ②③④ D. ①②
10.由函数y=logx与函数y=log(x-2)的图像及y= -2与y=3所围成的图形的面积为( )
A.10 B.15 C.20 D.25
二、填空题(每小题5分,共25分)
11. 已知幂函数的图象经过点(9,3),则
12.
13. 已知函数y=,则其单调递增区间是
14. 已知是方程的根,是方程的根,则值为
15.给出下列说法:①幂函数的图象一定不过第四象限;②奇函数图象一定过坐标原点;
③的递增区间为;④的单调减区间是;
⑤函数是非奇非偶函数。正确的有__ _______
三、解答题
16.(本小题12分)
已知全集,,,求的值。
17. (本小题12分)
的定义域为,的定义域为Q,
求及.
18.(本小题12分)
已知奇函数,在时的图象是如图所示的抛物线的一部分,
(1)请补全函数的图象
(2)求函数的表达式。
19.(本小题12分)
某企业为适应市场需求,准备投入资金16万元生产R和W型两种产品。经市场预测,生产R型产品所获利润y(万元)与投入资金x(万元)满足关系y=,生产W型产品所获利润y(万元)与投入资金x(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5万元。为获得最大总利润,问生产R、W型产品各应投入资金多少万元?获得的最大总利润Q是多少?
20.(本小题13分)
设函数,
(1)若,求的取值范围;
(2)求的最值,并给出取得最值时对应的的值;
(3)讨论函数的单调性。
21. (本小题14分)
已知函数
(1)若且函数的值域为,求的表达式;
(2)在(1)的条件下, 当时, 是单调函数, 求实数k的取值范围;
(3)设, 且为偶函数, 判断+能否大于零?请说明理由。
南康中学2012~2013学年度第一学期高一期中考试
数学参考答案
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
D
C
D
A
C
A
D
A
二、填空题(每小题5分,共25分)
11、10 12、16 13、 14、3 15、①
三、解答题
16、解:据题意,有,即 ……………………2分
解得或 …………………………6分
当时, 不合题意 ………………8分
当时, 适合 ……………………10分
……………………12分
17 解:由…………4分
由 ………………8分
………………10分
………………12分
18.解:(1)
…………………………6分
(2)当时,设把代入得
………………9分
当时,由图像或利用奇函数可得 ………………11分
……………………12分
19. 解:设生产R型产品投入资金为x万元,则生产W型产品的投入资金为(16-x)万元…2分
则…………………………6分
令, 则 ………………8分
所以 ,即(万元),Q取最大值,(万元)
此时,16-x=15(万元) ………………11分
答:生产R型产品投入资金为1万元,生产W型产品的投入资金为15万元,
获得的最大总利润是万元 ……………………12分
20.解:⑴且在是增函数
………………3分
即 ……………………4分
⑵
令,则 ………………6分
函数对称轴为
当即即时, ………………7分
当即即时, ……………………8分
⑶
令,则 ………………9分
函数在上是增函数 ………………10分
函数在即在是减函数
在时,是增函数 ………………12分
原函数在上是减函数,在是增函数 ………………13分
21.解:(1) ∵,
∴ ① ……1分
又函数的值域为, 所以
且 ②
由①②得
………3分
∴.
∴ ……5分
(2) 由(1)有
, ………7分
函数的对称轴为x=
函数g(x)是上的单调函数,或,
或 ……9分
(3) ∵是偶函数 ………………10分
∴ ∴, ……11分
∵又
∴+,
∴+能大于零. ………14分
