2021-2022学年苏科版九年级下《第7章 锐角三角函数》章末强化训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级下《第7章 锐角三角函数》章末强化训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 396.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 22:19:55 | ||
图片预览



文档简介
2021-2022学年苏科版九年级下《第7章 锐角三角函数》章末强化训练
(时间:90分钟 满分:120分)
一.选择题(共30分)
1.如图,△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( )
A.sinA= B.cosA= C.sinA= D.tanA=
第1题图 第2题图 第5题图 第7题图 第8题图 第9题图
2.如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα=,则tanα=( )
A. B. C. D.
3.tan45°sin45°-2sin30°cos45°+tan30°=( )
A. B. C. D.
4.在△ABC中,已知∠A,∠B都是锐角,+(1-tanB)2=0,那么∠C的度数为( ) A.75° B.90° C.105° D.120°
5.如图,AC是旗杆AB的一根拉线,测得AC=6 m,∠ACB=50°,则BC的长为( )
A.6cos50° m B.6sin50° m C. m D. m
6.已知抛物线y=-x2-2x+3与x轴交于A,B两点,将这条抛物线的顶点记为C,连结AC,则tan∠CAB的值为( )
A. B. C. D. 2
7.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,则=( )
A. sin∠ABC B. cos∠ABC C. tan∠ABC D. sinA
8. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为( )
A. B. C. D.
9.如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3.若∠B+∠B′=90°,则△ABC与△A′B′C′的面积之比为( )
A. 25∶9 B. 5∶3 C. ∶ D. 5 ∶3
10.关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ,tan(α+β)=(1-tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°·cos60°+cos30°sin60°=×+×=1.
利用上述公式计算下列三角函数:①sin105°=;②tan105°=-2-;③sin15°=;④cos90°=0.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共30分)
11.△ABC中,AB=AC,sinA=,则tanB= .
12.如图,在四边形ABCD中,AB=,AD=7,BC=8,tan∠B=,∠C=∠D,则线段CD的长为 .
第12题图 第13题图 第14题图 第15题图
13.如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为 .
14.如图,在笔直的海岸线l上有两个观测点A和B,点A在点B的正西方向,AB=2km.若从点A测得船C在北偏东60°的方向,从点B测得船C在北偏东45°的方向,则船C离海岸线l的距离为 km.(结果保留根号)
15.如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC于点E,若BD=8,sin∠CBD=,则AE的长为 .
16.已知α是锐角,tan(α+20°)=3,则α=___度.
17.如图将∠BAC放置在5×5的正方形网格中,顶点A在格点上.则sin∠BAC的值为____.
第17题图 第19题图 第20题图
18.在Rt△ABC中,∠C=90°,若cosB=,则tanB=____.
19.如图P(12,a)在反比例函数y=的图象上,PH⊥x轴于H,则tan∠POH的值为__
如图,在△ABC中,sinB=,BC=2,D是BC的中点,AC=2AD,则AB的长为____.
三.解答题(共60分)
21.(6分)在Rt△ABC中,已知∠C=90°,AB=15,AC=9,分别求出sinA和tanB的值.
22.(6分)计算:
(1)sin230°+sin60°-sin245°+cos230°; (2).
23.(6分)已知:,,求的算术平方根.
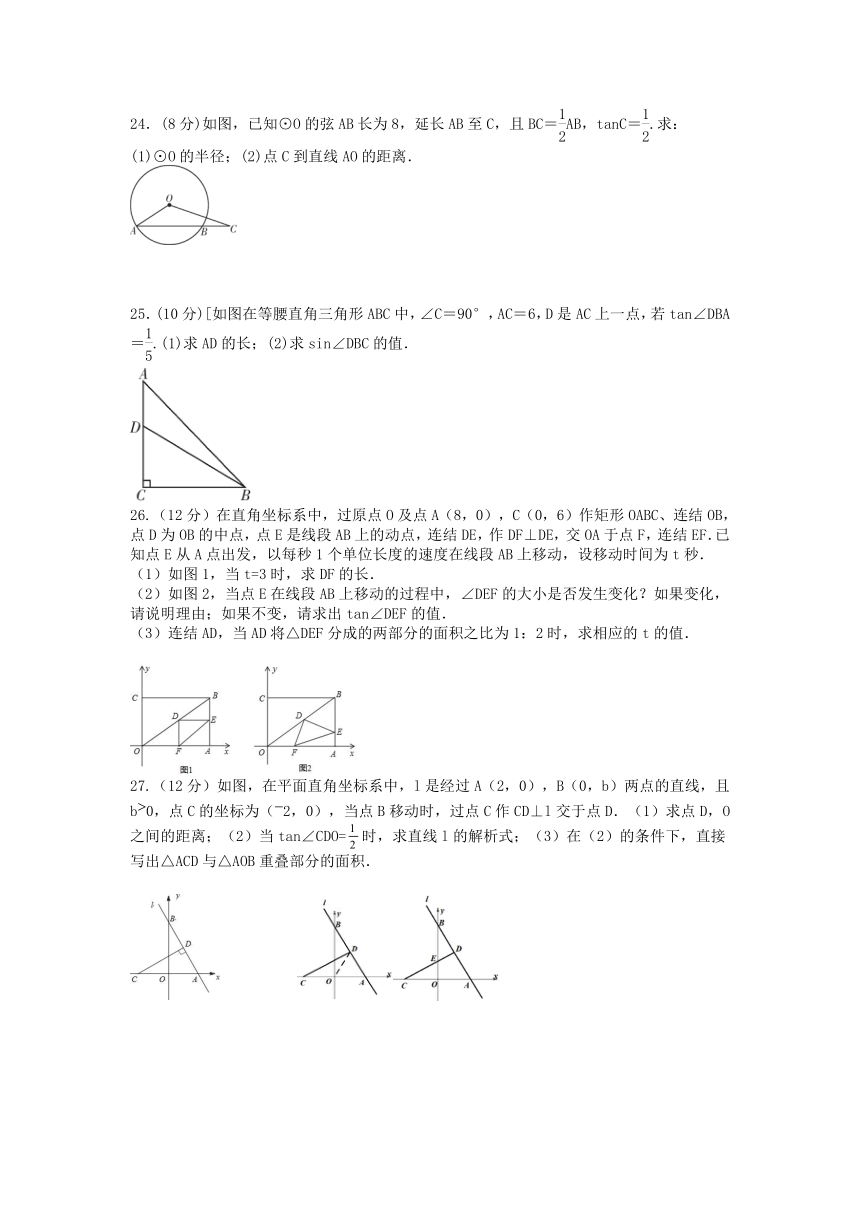
24.(8分)如图,已知⊙O的弦AB长为8,延长AB至C,且BC=AB,tanC=.求:
(1)⊙O的半径;(2)点C到直线AO的距离.
25.(10分)[如图在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=.(1)求AD的长;(2)求sin∠DBC的值.
26.(12分)在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
27.(12分)如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.(1)求点D,O之间的距离;(2)当tan∠CDO=时,求直线l的解析式;(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
教师样卷
一.选择题(共30分)
1.如图,△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( D )
A.sinA= B.cosA= C.sinA= D.tanA=
【解析】 ∵△ABC中,∠C=90°,BC=2,AB=3,∴AC===,sinA=,cosA=,tanA==,只有选项D正确.
第1题图 第2题图 第5题图 第7题图 第8题图 第9题图
2.如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα=,则tanα=( C)
A. B. C. D.
【解析】 如答图,作PQ⊥x轴,由sinα==,可设PQ=4a,OP=5a,∵OQ=3,∴由OQ2+PQ2=OP2,可得32+(4a)2=(5a)2,解得a=1(负值舍去),∴PQ=4,OP=5,则tanα==.
3.tan45°sin45°-2sin30°cos45°+tan30°=( D )
A. B. C. D.
【解析】 原式=1×-2××+=.
4.在△ABC中,已知∠A,∠B都是锐角,+(1-tanB)2=0,那么∠C的度数为( C )
A.75° B.90° C.105° D.120°
【解析】 ∵+(1-tanB)2=0,∴=0,(1-tanB)2=0,∴sinA=,tanB=1,∴∠A=30°,∠B=45°,∴∠C的度数为180°-30°-45°=105°.
5.如图,AC是旗杆AB的一根拉线,测得AC=6 m,∠ACB=50°,则BC的长为( A )
A.6cos50° m B.6sin50° m C. m D. m
6.已知抛物线y=-x2-2x+3与x轴交于A,B两点,将这条抛物线的顶点记为C,连结AC,则tan∠CAB的值为(D)
A. B. C. D. 2
7.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,则=(A)
A. sin∠ABC B. cos∠ABC C. tan∠ABC D. sinA
【解】 提示:过点D作DE⊥AB于点E,证BE=BC.
8. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为(B)
A. B. C. D.
【解】 设AC=x,则AB==,AD==, ∴==.
9.如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3.若∠B+∠B′=90°,则△ABC与△A′B′C′的面积之比为(A)
A. 25∶9 B. 5∶3 C. ∶ D. 5 ∶3
【解】 如解图.过点A 作AD⊥BC于点D,过点A′作A′D′⊥B′C′于点D′.∵AB=AC,A′B′=A′C′,∴∠B=∠C,∠B′=∠C′,BC=2BD,B′C′=2B′D′,∴AD=AB·sinB,A′D′=A′B′·sinB′,BC=2BD=2AB·cosB,B′C′=2B′D′=2A′B′·cosB′.
∵∠B+∠B′=90°,∴sinB=cosB′,sinB′=cosB.∵S△ABC=AD·BC=AB·sinB·2AB·cosB=25sinB·cosB,S△A′B′C′=A′D′·B′C′=A′B′·sinB′·2A′B′·cosB′=9sinB′·cosB′,
∴S△ABC∶S△A′B′C′=25∶9.
10.关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ,tan(α+β)=(1-tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°·cos60°+cos30°sin60°=×+×=1.
利用上述公式计算下列三角函数:①sin105°=;②tan105°=-2-;③sin15°=;④cos90°=0.其中正确的个数有( D )
A.1个 B.2个 C.3个 D.4个
【解析】 ①sin105°=sin(45°+60°)=sin60°cos45°+cos60°sin45°=×+×=,故此选项正确;②tan105°=tan(60°+45°)===-2-,故此选项正确;③sin15°=sin(60°-45°)=sin60°cos45°-cos60°sin45°=×-×=,故此选项正确;④cos90°=cos(45°+45°)=cos45°cos45°-sin45°sin45°=×-×=0,故此选项正确.故正确的有4个,故选D.
二.填空题(共30分)
11.△ABC中,AB=AC,sinA=,则tanB= .【答案】
12.如图,在四边形ABCD中,AB=,AD=7,BC=8,tan∠B=,∠C=∠D,则线段CD的长为 .【答案】..
第12题图 第13题图 第14题图 第15题图
13.如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为 .【答案】.5..
14.如图,在笔直的海岸线l上有两个观测点A和B,点A在点B的正西方向,AB=2km.若从点A测得船C在北偏东60°的方向,从点B测得船C在北偏东45°的方向,则船C离海岸线l的距离为 km.(结果保留根号)【答案】.1+.
15.如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC于点E,若BD=8,sin∠CBD=,则AE的长为 .【答案】.9.
16.已知α是锐角,tan(α+20°)=3,则α=__40__度.
【解析】 tan(α+20°)=3,则tan(α+20°)=,故α+20°=60°,则α=40°.
17.如图将∠BAC放置在5×5的正方形网格中,顶点A在格点上.则sin∠BAC的值为____.
【解析】 如答图所示,连结BC,∵AB=BC=,AC=2,∴AB2+BC2=AC2,∴∠ABC=90°,∴∠BAC=∠ACB=45°,∴sin∠BAC=.
第17题图 第19题图 第20题图
18.在Rt△ABC中,∠C=90°,若cosB=,则tanB=____.
【解析】 如答图,∵在Rt△ABC中,∠C=90°,cosB=,∴设BC=4x,AB=5x,由勾股定理得AC==3x,∴tanB==.
19.如图P(12,a)在反比例函数y=的图象上,PH⊥x轴于H,则tan∠POH的值为____.
【解析】 ∵P(12,a)在反比例函数y=的图象上,∴a==5,∵PH⊥x轴于H,∴PH=5,OH=12,∴tan∠POH=.
如图,在△ABC中,sinB=,BC=2,D是BC的中点,AC=2AD,则AB的长为____.
【解析】 如答图,过A作AE⊥BC于E,∵sinB==,
设AE=4x,AB=5x,∴BE=3x,∵D是BC的中点,BC=2,∴BD=1,∴ED=1-3x,CE=2-3x,∵AC=2AD,∴AC2=4AD2,由勾股定理得AE2+CE2=4(AE2+DE2),∴(4x)2+(2-3x)2=4[(4x)2+(1-3x)2],解得x=0(舍)或,∴AB=5×=.
三.解答题(共60分)
21.(6分)在Rt△ABC中,已知∠C=90°,AB=15,AC=9,分别求出sinA和tanB的值.
解:如答图,∵∠C=90°,AB=15,AC=9,∴BC==12,∴sinA==,tanB==.
22.(6分)计算:
(1)sin230°+sin60°-sin245°+cos230°; (2).
解:(1)原式=+-+=+-+=;
(2)原式==.
23.(6分)已知:,,求的算术平方根.
解:,
.
.
.
24.(8分)如图,已知⊙O的弦AB长为8,延长AB至C,且BC=AB,tanC=.求:
(1)⊙O的半径;(2)点C到直线AO的距离.
解:(1)如答图①,过点O作OD⊥AB于D,则∠ODC=90°,∵OD过点O,∴AD=BD,∵AB=8,∴AD=BD=4,∵BC=AB,∴BC=4,∴DC=4+4=8,∵tanC==,∴OD=4,在Rt△ODA中,由勾股定理得OA===4,即⊙O的半径是4;
① ②
(2)如答图②,过点C作CE⊥AO于E,则S△AOC=·AC·OD=·AO·CE,即×12×4=×4·CE,解得CE=6,即点C到直线AO的距离是6.
25.(10分)[如图在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=.(1)求AD的长;(2)求sin∠DBC的值.
解:(1)如答图,过点D作DH⊥AB于点H,∵△ABC为等腰直角三角形,∠C=90°,∴∠A=45°,∴AH=DH,设AH=x,∴DH=x,∵tan∠DBA=,∴BH=5x,∴AB=6x,∵AC=6,∴由勾股定理可知AB=6,∴x=,∴AH=DH=,∴由勾股定理可知AD=2;
(2)∵AD=2,∴DC=4,∴由勾股定理可知DB=2,∴sin∠DBC==.
26.(12分)在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
【答案】(1)3;(2)∠DEF的大小不变,tan∠DEF=;(3)或.
解:(1)当t=3时,点E为AB的中点,∵A(8,0),C(0,6),∴OA=8,OC=6,
∵点D为OB的中点,∴DE∥OA,DE=OA=4,∵四边形OABC是矩形,∴OA⊥AB,∴DE⊥AB,
∴∠OAB=∠DEA=90°,又∵DF⊥DE,∴∠EDF=90°,∴四边形DFAE是矩形,∴DF=AE=3;
(2)∠DEF的大小不变;理由如下:作DM⊥OA于M,DN⊥AB于N,如图2所示:∵四边形OABC是矩形,∴OA⊥AB,∴四边形DMAN是矩形,∴∠MDN=90°,DM∥AB,DN∥OA,
∴, ,∵点D为OB的中点,∴M、N分别是OA、AB的中点,∴DM=AB=3,DN=OA=4,∵∠EDF=90°,∴∠FDM=∠EDN,又∵∠DMF=∠DNE=90°,∴△DMF∽△DNE,
∴,∵∠EDF=90°,∴tan∠DEF=;
(3)作DM⊥OA于M,DN⊥AB于N,若AD将△DEF的面积分成1:2的两部分,设AD交EF于点G,则点G为EF的三等分点;①当点E到达中点之前时,如图3所示,NE=3﹣t,
由△DMF∽△DNE得:MF=(3﹣t),∴AF=4+MF=﹣t+,∵点G为EF的三等分点,
∴G(,),设直线AD的解析式为y=kx+b,把A(8,0),D(4,3)代入得: ,
解得: ,∴直线AD的解析式为y=﹣x+6,把G(,)代入得:t=;
②当点E越过中点之后,如图4所示,NE=t﹣3,由△DMF∽△DNE得:MF=(t﹣3),
∴AF=4﹣MF=﹣t+,∵点G为EF的三等分点,∴G(,),代入直线AD的解析式y=﹣x+6得:t=;综上所述,当AD将△DEF分成的两部分的面积之比为1:2时,t的值为或.
27.(12分)如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.(1)求点D,O之间的距离;(2)当tan∠CDO=时,求直线l的解析式;(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
【答案】(1)2;(2);(3)
解:解:(1)连接OD,,. , ,
;(2), .
,., ,
.,,,.
设直线l的解析式为,将代入解析式中得,解得,
∴直线l解析式为;
设CD与y轴的交点为E, ,
,. ,
,∴△ACD与△AOB重叠部分的面积为.
(时间:90分钟 满分:120分)
一.选择题(共30分)
1.如图,△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( )
A.sinA= B.cosA= C.sinA= D.tanA=
第1题图 第2题图 第5题图 第7题图 第8题图 第9题图
2.如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα=,则tanα=( )
A. B. C. D.
3.tan45°sin45°-2sin30°cos45°+tan30°=( )
A. B. C. D.
4.在△ABC中,已知∠A,∠B都是锐角,+(1-tanB)2=0,那么∠C的度数为( ) A.75° B.90° C.105° D.120°
5.如图,AC是旗杆AB的一根拉线,测得AC=6 m,∠ACB=50°,则BC的长为( )
A.6cos50° m B.6sin50° m C. m D. m
6.已知抛物线y=-x2-2x+3与x轴交于A,B两点,将这条抛物线的顶点记为C,连结AC,则tan∠CAB的值为( )
A. B. C. D. 2
7.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,则=( )
A. sin∠ABC B. cos∠ABC C. tan∠ABC D. sinA
8. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为( )
A. B. C. D.
9.如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3.若∠B+∠B′=90°,则△ABC与△A′B′C′的面积之比为( )
A. 25∶9 B. 5∶3 C. ∶ D. 5 ∶3
10.关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ,tan(α+β)=(1-tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°·cos60°+cos30°sin60°=×+×=1.
利用上述公式计算下列三角函数:①sin105°=;②tan105°=-2-;③sin15°=;④cos90°=0.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共30分)
11.△ABC中,AB=AC,sinA=,则tanB= .
12.如图,在四边形ABCD中,AB=,AD=7,BC=8,tan∠B=,∠C=∠D,则线段CD的长为 .
第12题图 第13题图 第14题图 第15题图
13.如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为 .
14.如图,在笔直的海岸线l上有两个观测点A和B,点A在点B的正西方向,AB=2km.若从点A测得船C在北偏东60°的方向,从点B测得船C在北偏东45°的方向,则船C离海岸线l的距离为 km.(结果保留根号)
15.如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC于点E,若BD=8,sin∠CBD=,则AE的长为 .
16.已知α是锐角,tan(α+20°)=3,则α=___度.
17.如图将∠BAC放置在5×5的正方形网格中,顶点A在格点上.则sin∠BAC的值为____.
第17题图 第19题图 第20题图
18.在Rt△ABC中,∠C=90°,若cosB=,则tanB=____.
19.如图P(12,a)在反比例函数y=的图象上,PH⊥x轴于H,则tan∠POH的值为__
如图,在△ABC中,sinB=,BC=2,D是BC的中点,AC=2AD,则AB的长为____.
三.解答题(共60分)
21.(6分)在Rt△ABC中,已知∠C=90°,AB=15,AC=9,分别求出sinA和tanB的值.
22.(6分)计算:
(1)sin230°+sin60°-sin245°+cos230°; (2).
23.(6分)已知:,,求的算术平方根.
24.(8分)如图,已知⊙O的弦AB长为8,延长AB至C,且BC=AB,tanC=.求:
(1)⊙O的半径;(2)点C到直线AO的距离.
25.(10分)[如图在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=.(1)求AD的长;(2)求sin∠DBC的值.
26.(12分)在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
27.(12分)如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.(1)求点D,O之间的距离;(2)当tan∠CDO=时,求直线l的解析式;(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
教师样卷
一.选择题(共30分)
1.如图,△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( D )
A.sinA= B.cosA= C.sinA= D.tanA=
【解析】 ∵△ABC中,∠C=90°,BC=2,AB=3,∴AC===,sinA=,cosA=,tanA==,只有选项D正确.
第1题图 第2题图 第5题图 第7题图 第8题图 第9题图
2.如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα=,则tanα=( C)
A. B. C. D.
【解析】 如答图,作PQ⊥x轴,由sinα==,可设PQ=4a,OP=5a,∵OQ=3,∴由OQ2+PQ2=OP2,可得32+(4a)2=(5a)2,解得a=1(负值舍去),∴PQ=4,OP=5,则tanα==.
3.tan45°sin45°-2sin30°cos45°+tan30°=( D )
A. B. C. D.
【解析】 原式=1×-2××+=.
4.在△ABC中,已知∠A,∠B都是锐角,+(1-tanB)2=0,那么∠C的度数为( C )
A.75° B.90° C.105° D.120°
【解析】 ∵+(1-tanB)2=0,∴=0,(1-tanB)2=0,∴sinA=,tanB=1,∴∠A=30°,∠B=45°,∴∠C的度数为180°-30°-45°=105°.
5.如图,AC是旗杆AB的一根拉线,测得AC=6 m,∠ACB=50°,则BC的长为( A )
A.6cos50° m B.6sin50° m C. m D. m
6.已知抛物线y=-x2-2x+3与x轴交于A,B两点,将这条抛物线的顶点记为C,连结AC,则tan∠CAB的值为(D)
A. B. C. D. 2
7.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,则=(A)
A. sin∠ABC B. cos∠ABC C. tan∠ABC D. sinA
【解】 提示:过点D作DE⊥AB于点E,证BE=BC.
8. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为(B)
A. B. C. D.
【解】 设AC=x,则AB==,AD==, ∴==.
9.如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3.若∠B+∠B′=90°,则△ABC与△A′B′C′的面积之比为(A)
A. 25∶9 B. 5∶3 C. ∶ D. 5 ∶3
【解】 如解图.过点A 作AD⊥BC于点D,过点A′作A′D′⊥B′C′于点D′.∵AB=AC,A′B′=A′C′,∴∠B=∠C,∠B′=∠C′,BC=2BD,B′C′=2B′D′,∴AD=AB·sinB,A′D′=A′B′·sinB′,BC=2BD=2AB·cosB,B′C′=2B′D′=2A′B′·cosB′.
∵∠B+∠B′=90°,∴sinB=cosB′,sinB′=cosB.∵S△ABC=AD·BC=AB·sinB·2AB·cosB=25sinB·cosB,S△A′B′C′=A′D′·B′C′=A′B′·sinB′·2A′B′·cosB′=9sinB′·cosB′,
∴S△ABC∶S△A′B′C′=25∶9.
10.关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ,cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ,tan(α+β)=(1-tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°·cos60°+cos30°sin60°=×+×=1.
利用上述公式计算下列三角函数:①sin105°=;②tan105°=-2-;③sin15°=;④cos90°=0.其中正确的个数有( D )
A.1个 B.2个 C.3个 D.4个
【解析】 ①sin105°=sin(45°+60°)=sin60°cos45°+cos60°sin45°=×+×=,故此选项正确;②tan105°=tan(60°+45°)===-2-,故此选项正确;③sin15°=sin(60°-45°)=sin60°cos45°-cos60°sin45°=×-×=,故此选项正确;④cos90°=cos(45°+45°)=cos45°cos45°-sin45°sin45°=×-×=0,故此选项正确.故正确的有4个,故选D.
二.填空题(共30分)
11.△ABC中,AB=AC,sinA=,则tanB= .【答案】
12.如图,在四边形ABCD中,AB=,AD=7,BC=8,tan∠B=,∠C=∠D,则线段CD的长为 .【答案】..
第12题图 第13题图 第14题图 第15题图
13.如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为 .【答案】.5..
14.如图,在笔直的海岸线l上有两个观测点A和B,点A在点B的正西方向,AB=2km.若从点A测得船C在北偏东60°的方向,从点B测得船C在北偏东45°的方向,则船C离海岸线l的距离为 km.(结果保留根号)【答案】.1+.
15.如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC于点E,若BD=8,sin∠CBD=,则AE的长为 .【答案】.9.
16.已知α是锐角,tan(α+20°)=3,则α=__40__度.
【解析】 tan(α+20°)=3,则tan(α+20°)=,故α+20°=60°,则α=40°.
17.如图将∠BAC放置在5×5的正方形网格中,顶点A在格点上.则sin∠BAC的值为____.
【解析】 如答图所示,连结BC,∵AB=BC=,AC=2,∴AB2+BC2=AC2,∴∠ABC=90°,∴∠BAC=∠ACB=45°,∴sin∠BAC=.
第17题图 第19题图 第20题图
18.在Rt△ABC中,∠C=90°,若cosB=,则tanB=____.
【解析】 如答图,∵在Rt△ABC中,∠C=90°,cosB=,∴设BC=4x,AB=5x,由勾股定理得AC==3x,∴tanB==.
19.如图P(12,a)在反比例函数y=的图象上,PH⊥x轴于H,则tan∠POH的值为____.
【解析】 ∵P(12,a)在反比例函数y=的图象上,∴a==5,∵PH⊥x轴于H,∴PH=5,OH=12,∴tan∠POH=.
如图,在△ABC中,sinB=,BC=2,D是BC的中点,AC=2AD,则AB的长为____.
【解析】 如答图,过A作AE⊥BC于E,∵sinB==,
设AE=4x,AB=5x,∴BE=3x,∵D是BC的中点,BC=2,∴BD=1,∴ED=1-3x,CE=2-3x,∵AC=2AD,∴AC2=4AD2,由勾股定理得AE2+CE2=4(AE2+DE2),∴(4x)2+(2-3x)2=4[(4x)2+(1-3x)2],解得x=0(舍)或,∴AB=5×=.
三.解答题(共60分)
21.(6分)在Rt△ABC中,已知∠C=90°,AB=15,AC=9,分别求出sinA和tanB的值.
解:如答图,∵∠C=90°,AB=15,AC=9,∴BC==12,∴sinA==,tanB==.
22.(6分)计算:
(1)sin230°+sin60°-sin245°+cos230°; (2).
解:(1)原式=+-+=+-+=;
(2)原式==.
23.(6分)已知:,,求的算术平方根.
解:,
.
.
.
24.(8分)如图,已知⊙O的弦AB长为8,延长AB至C,且BC=AB,tanC=.求:
(1)⊙O的半径;(2)点C到直线AO的距离.
解:(1)如答图①,过点O作OD⊥AB于D,则∠ODC=90°,∵OD过点O,∴AD=BD,∵AB=8,∴AD=BD=4,∵BC=AB,∴BC=4,∴DC=4+4=8,∵tanC==,∴OD=4,在Rt△ODA中,由勾股定理得OA===4,即⊙O的半径是4;
① ②
(2)如答图②,过点C作CE⊥AO于E,则S△AOC=·AC·OD=·AO·CE,即×12×4=×4·CE,解得CE=6,即点C到直线AO的距离是6.
25.(10分)[如图在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=.(1)求AD的长;(2)求sin∠DBC的值.
解:(1)如答图,过点D作DH⊥AB于点H,∵△ABC为等腰直角三角形,∠C=90°,∴∠A=45°,∴AH=DH,设AH=x,∴DH=x,∵tan∠DBA=,∴BH=5x,∴AB=6x,∵AC=6,∴由勾股定理可知AB=6,∴x=,∴AH=DH=,∴由勾股定理可知AD=2;
(2)∵AD=2,∴DC=4,∴由勾股定理可知DB=2,∴sin∠DBC==.
26.(12分)在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
【答案】(1)3;(2)∠DEF的大小不变,tan∠DEF=;(3)或.
解:(1)当t=3时,点E为AB的中点,∵A(8,0),C(0,6),∴OA=8,OC=6,
∵点D为OB的中点,∴DE∥OA,DE=OA=4,∵四边形OABC是矩形,∴OA⊥AB,∴DE⊥AB,
∴∠OAB=∠DEA=90°,又∵DF⊥DE,∴∠EDF=90°,∴四边形DFAE是矩形,∴DF=AE=3;
(2)∠DEF的大小不变;理由如下:作DM⊥OA于M,DN⊥AB于N,如图2所示:∵四边形OABC是矩形,∴OA⊥AB,∴四边形DMAN是矩形,∴∠MDN=90°,DM∥AB,DN∥OA,
∴, ,∵点D为OB的中点,∴M、N分别是OA、AB的中点,∴DM=AB=3,DN=OA=4,∵∠EDF=90°,∴∠FDM=∠EDN,又∵∠DMF=∠DNE=90°,∴△DMF∽△DNE,
∴,∵∠EDF=90°,∴tan∠DEF=;
(3)作DM⊥OA于M,DN⊥AB于N,若AD将△DEF的面积分成1:2的两部分,设AD交EF于点G,则点G为EF的三等分点;①当点E到达中点之前时,如图3所示,NE=3﹣t,
由△DMF∽△DNE得:MF=(3﹣t),∴AF=4+MF=﹣t+,∵点G为EF的三等分点,
∴G(,),设直线AD的解析式为y=kx+b,把A(8,0),D(4,3)代入得: ,
解得: ,∴直线AD的解析式为y=﹣x+6,把G(,)代入得:t=;
②当点E越过中点之后,如图4所示,NE=t﹣3,由△DMF∽△DNE得:MF=(t﹣3),
∴AF=4﹣MF=﹣t+,∵点G为EF的三等分点,∴G(,),代入直线AD的解析式y=﹣x+6得:t=;综上所述,当AD将△DEF分成的两部分的面积之比为1:2时,t的值为或.
27.(12分)如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.(1)求点D,O之间的距离;(2)当tan∠CDO=时,求直线l的解析式;(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
【答案】(1)2;(2);(3)
解:解:(1)连接OD,,. , ,
;(2), .
,., ,
.,,,.
设直线l的解析式为,将代入解析式中得,解得,
∴直线l解析式为;
设CD与y轴的交点为E, ,
,. ,
,∴△ACD与△AOB重叠部分的面积为.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
