安徽省合肥市包河区九年级下学期开学考试数学试题 (word版含答案)
文档属性
| 名称 | 安徽省合肥市包河区九年级下学期开学考试数学试题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 526.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 08:46:33 | ||
图片预览



文档简介
安徽省合肥市包河区九年级下学期开学考试数学试题
一、单选题
1.新型冠状病毒疫情引起全国人民的关注,在社会各界贡献力量的同时,演艺圈也进行着公益接力.据有关报道称:截至2月16日20点,演艺圈人士共捐赠口罩近300万个,募集善款金额达到约577 000 000元.数据“577 000 000”用科学记数法表示为( )
A. B. C. D.
2.图中的内容是某同学完成的作业,嘉琪帮他做了批改,嘉琪批改正确的题数是( )
A.2个 B.3个 C.4个 D.5个
3.如图,梯形中,点在上,点是的中点,且若则的长为( )
A. B. C. D.
4.如图1是一座立交桥的示意图(道路宽度忽略不计),A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF;弯道为以点O为圆心的一段弧,且,,所对的圆心角为90o.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出,其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法正确的是( )
A.甲车在立交桥上共行驶9s
B.从F口出比从G口出多行驶40m
C.甲车从F口出,乙车从G口出
D.立交桥总长为120m
5.将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个正方形重叠形成的重叠部分的面积和为( )
A.cm2 B.cm2 C. cm2 D.()ncm2
6.分式方程的根是( )
A. B. C. D.
7.如图,长方形中有两个半圆和一个圆,已知长方形宽为,则阴影部分的面积为( )
A. B. C. D.
8.如图,在同一直线上,≌,,,则的值为( )
A. B. C. D.
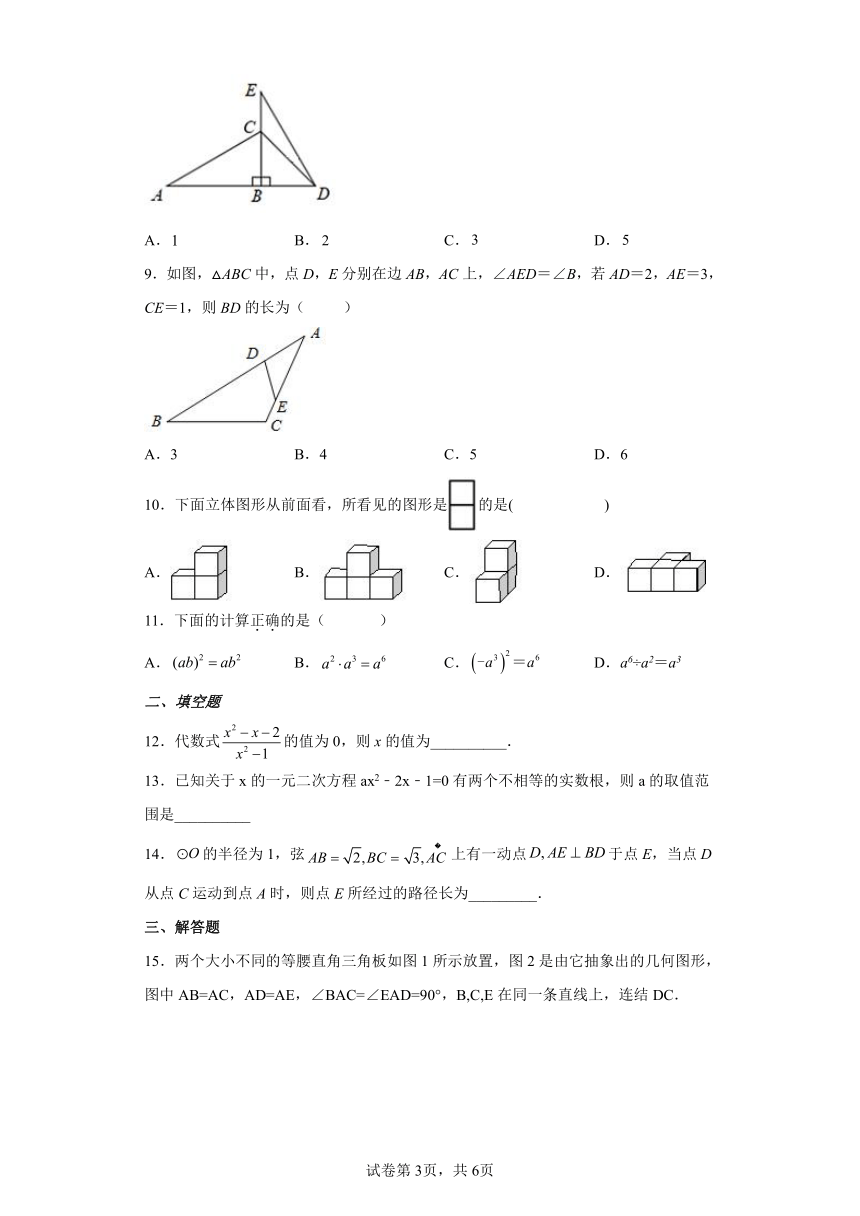
9.如图,△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,若AD=2,AE=3,CE=1,则BD的长为( )
A.3 B.4 C.5 D.6
10.下面立体图形从前面看,所看见的图形是的是( )
A. B. C. D.
11.下面的计算正确的是( )
A. B. C. D.a6÷a2=a3
二、填空题
12.代数式的值为0,则x的值为__________.
13.已知关于x的一元二次方程ax2﹣2x﹣1=0有两个不相等的实数根,则a的取值范围是__________
14.的半径为1,弦上有一动点于点E,当点D从点C运动到点A时,则点E所经过的路径长为_________.
三、解答题
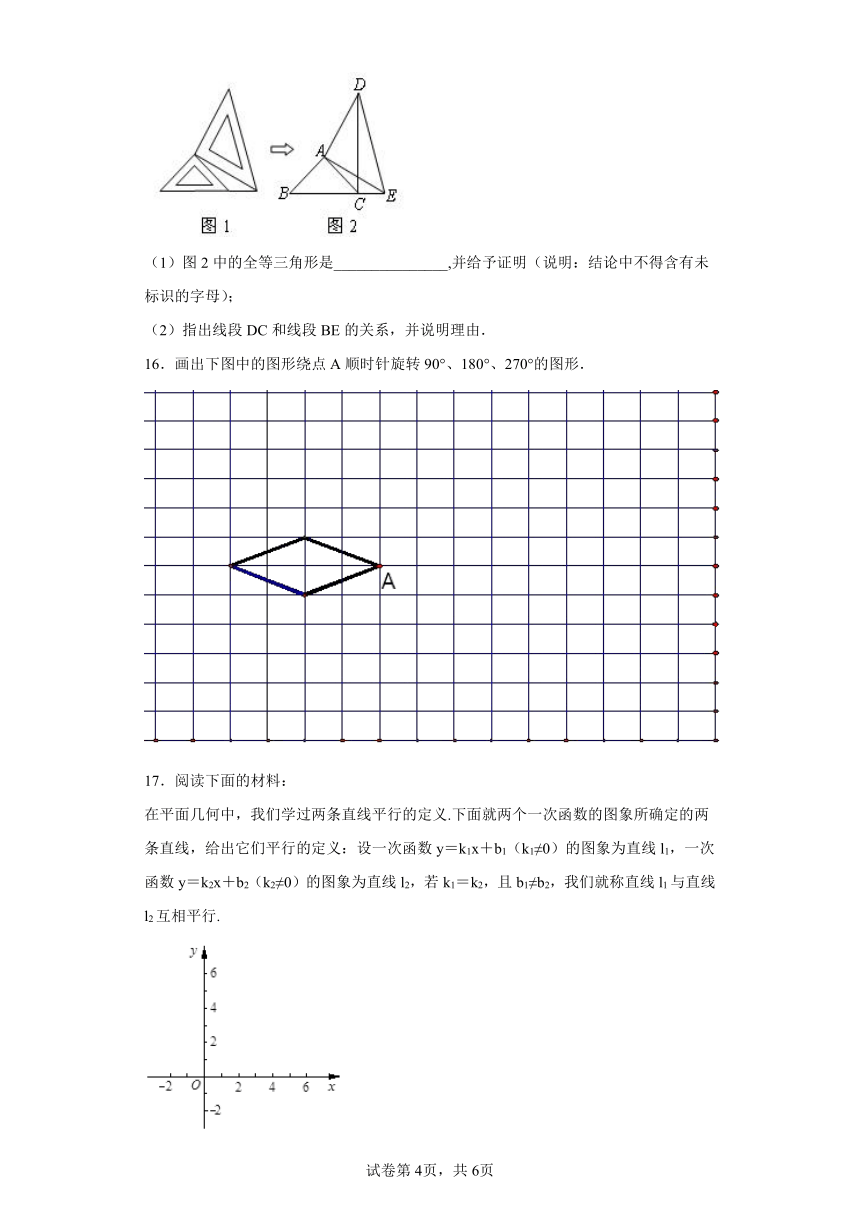
15.两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
16.画出下图中的图形绕点A顺时针旋转90°、180°、270°的图形.
17.阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
18.用适当的方法解方程:
(1);
(2).
19.某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元.为了扩大销售量,增加盈利,尽快减少库存,商场采取适当的降价措施.经调查发现,如果每件降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)该商场平均每天盈利能达到1500元吗?如果能,求出此时应降价多少;如果不能,请说明理由;
(3)该商场平均每天盈利最多多少元?达到最大值时应降价多少元?
20.正数x的两个平方根分别为3﹣a和2a+7.
(1)求a的值;
(2)求44﹣x这个数的立方根.
21.在武胜县中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生棵根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.
请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 人,表示最喜爱甲类图书的人数扇形的圆心角的度数是 ;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的倍,若这所学校共有学生人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
22.小明家所在居民楼的对面有一座大厦AB=74米,为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
(1)求小明家所在居民楼与大厦的距离CD的长度.(参考数据:sin37°≈,tan37°≈,sin48°≈,tan48°≈)
(2)冬季,在阳光的照射下测得一根1m长的竹竿在地面的影长是1.6m,试问此时太阳光是否能直射到小明家?请通过计算说明.
23.如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是正方形,请直接给出OA应满足的条件是 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于577 000 000有9位,所以可以确定n=9-1=8.
【详解】
577 000 000 =5.77×108.
故选:C.
【点睛】
此题考查科学记数法表示较大的数的方法,准确确定a与n值是关键.
2.B
【解析】
【分析】
分析各项计算得到结果,即可作出判断.
【详解】
①﹣1的倒数=﹣1,符合题意;
②1的平方根为±1,立方根等于本身,不符合题意;
③(﹣)2=,符合题意;
④|1﹣|=﹣1,符合题意;
⑤=﹣=﹣2,不符合题意,
故选:B.
【点睛】
此题主要考查对倒数、平方根、立方根以及绝对值的理解,熟练掌握,即可解题.
3.D
【解析】
【详解】
解:延长AF,交BC的延长线于G
∵AD∥BC
∴∠D=∠FCG
∵DF=FC,∠DFA=∠CFG
∴△ADF≌△GCF
∴CG=AD=2.7,FG=AF=4
∴AG=8
∵∠BAG=90°
∴
∵BE=AE
∴∠B=∠BAE
∵∠BAG=90°
∴∠B+∠G=90°,∠BAE+∠EAG=90°
∴∠G=∠EAG
∴EG=EA=EB
∴EG=5
∴EC=2.3
4.B
【解析】
【分析】
根据题意、结合图象问题可得.
【详解】
解:由图象可知,甲车驶出立交桥时,一共行驶的时间为3+2+3=8(s),故选项A不合题意;
根据两车运行路线,从F口驶出比从G口多走,弧长之和,用时为4s,则走40m,故选项B符合题意;
甲车先驶出立交桥,乙车后驶出立交桥,所以甲车从G口出,乙车从F口出,故选项C不合题意;
图中立交桥总长为:3×3×10+3×2×10=150(m),故选项D不合题意,
故选:B.
【点睛】
本题考查了动点问题的函数图象,理解题意、数形结合是解决问题的关键
5.B
【解析】
【分析】
根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n-1阴影部分的和.
【详解】
由题意可得阴影部分面积等于正方形面积的,即是,5个这样的正方形重叠部分(阴影部分)的面积和为×4,n个这样的正方形重叠部分(阴影部分)的面积和为×(n-1)=cm2.
故选B.
【点睛】
考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.
6.D
【解析】
【详解】
试题分析:方程的两边同乘,得:,解得.
检验:把代入.所以原方程的解为:.故选D.
考点:解分式方程.
7.C
【解析】
【分析】
如图,两个半圆和一个圆的直径都是相等为a,故可求出阴影部分的面积.
【详解】
解:由图形可知,
这两个半圆和一个圆的直径都相等是a,所以阴影部分的面积=2a2-2×圆的面积,
∴2a2-2×π×()2=2a2 =,
故选:C.
【点睛】
本题考查了列代数式问题,关键是得到阴影部分面积的等量关系.
8.C
【解析】
【分析】
设BD=x,根据全等的性质得到BC=x,故BE=AB=x+2,再根据得到方程即可求解.
【详解】
设BD=x
∵≌
∴BD=BC=x
∴BE=AB=x+2,
∵
∴AB+BD=8,即x+2+x=8
解得x=3
∴=EC×BD=×2×3=3
故选C.
【点睛】
此题主要考查全等的性质,解题的关键是熟知三角形的性质及三角形的面积公式.
9.B
【解析】
【详解】
∵AE=3,CE=1,
.
∵∠AED=∠B,∠A=∠A,
,
,
,
,
.
故选B.
10.C
【解析】
【详解】
根据题干分析可得:从前面看到的图形是 的是选项C中的图形,故选C.
11.C
【解析】
【分析】
根据幂的运算法则逐项计算即可.
【详解】
解:A. ,原选项不正确,不符合题意;
B. ,原选项不正确,不符合题意;
C. ,原选项正确,符合题意;
D. a6÷a2=a4,原选项不正确,不符合题意;
故选:C.
【点睛】
本题考查了幂的运算,解题关键是熟练运用幂的运算法则,准确进行计算.
12.2
【解析】
【分析】
根据分式值为0的条件:分子为0,分母不为0,列方程与不等式,求解即可.
【详解】
解:∵分式的值为零,
∴=0且,
=0
因式分解得
解方程得,;
解不等式得,或,
∴
故答案为:.
【点睛】
本题考查了分式值为零的条件,包含一元二次方程和一元一次不等式,解题关键是明确分式值为0,分子为0分母不为0,列出方程和不等式求解.
13.a>﹣1且a≠0
【解析】
【详解】
解∵关于的一元二次方程有两个不相等的实数根,
∴ ,解得:且.
即的取值范围是:且.
【点睛】
本题考查根据一元二次根的情况求参数.由本题题意可知字母的取值需同时满足2个条件:(1)由原方程是一元二次方程可知二次项系数;(2)由原方程有两个不相等的实数根可知,“根的判别式△的值大于0”.
14.或
【解析】
【分析】
利用定线AB所对得角是定角∠AEB=90°,可知点E得运动路径是以AB中点H为圆心,AH为半径的,注意求圆心角∠AHG的度数时分两种情况,AB,BC在圆心O的同侧或异侧.
【详解】
解:连接,,,过点作于点,
在中,,
动点的运动路径是以中点为圆心,为半径的,
分两种情况:
①,在圆心的同侧,
中,,
,,
在中,,
,
,得圆心角,
.
②,在圆心的异侧.
,得圆心角,
.
故答案为:或.
【点睛】
本题考查了90°的圆周角所对得弦是直径这一知识点得灵活运用,分类讨论的思想方法.
15.(1)△ACD≌△ABE,证明见解析;(2)线段DC和线段BE的关系是:垂直且相等,理由见解析.
【解析】
【分析】
(1)根据SAS证明△ACD≌△ABE 即可;
(2)线段DC和线段BE的关系是:垂直且相等.利用全等三角形的性质即可证明.
【详解】
解:(1)图2中的全等三角形是:△ACD≌△ABE.
证明:∵∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
∴∠BAE=∠CAD,
在△ABE与△ACD中,,
∴△ACD≌△ABE(SAS).
故答案为△ACD≌△ABE;
(2)线段DC和线段BE的关系是:垂直且相等.
理由:由(1)知:△ACD≌△ABE
∴DC=BE,∠ACD=∠B,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,即∠BCD=90°,
∴BE⊥DC,
∴线段DC和线段BE的关系是:垂直且相等.
【点睛】
本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
16.画图见解析.
【解析】
【分析】
根据旋转的特征,图形绕点A顺时针旋转90°、180°、270°,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可分别画出90°、180°、270°后的图形.
【详解】
画出图形绕点A顺时针旋转90°(红)、180°(绿)、270°(蓝)后的图形如图所示:
【点睛】
本题考查了旋转作图,旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.
17.(1)y=—2x+6,图象见详解:
(2)△的面积关于的函数表达式为
【解析】
【分析】
试题分析:(1)设直线l的函数表达式为y=k x+b,根据平行的性质可得k=—2,再根据直线l过点(1,4),即可求得直线l的函数表达式,最后根据描点法即可做出直线的图象;
(2)先分别求得直线l分别与y轴、x轴的交点A、B的坐标,再根据l∥,可设直线为y=—2x+t,从而表示出C点的坐标为(,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
【详解】
(1)设直线l的函数表达式为y=k x+b.
∵直线l与直线y=—2x—1平行,∴k=—2.
∵直线l过点(1,4),∴—2+b=4,∴b=6.
∴直线l的函数表达式为y=—2x+6,直线的图象如图:
(2)∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,6)、(3,0).
∵l∥,
∴直线为y=—2x+t.
∴C点的坐标为(,0).
∵t>0,
∴>0.
∴C点在x轴的正半轴上.
当C点在B点的左侧时,;
当C点在B点的右侧时,.
∴△的面积关于的函数表达式为
【点睛】
本题考查一次函数的综合题,本题知识点多,综合性强,难度较大,主要考查学生对一次函数的知识的熟练掌握情况.
18.(1);(2),
【解析】
【分析】
(1)利用配方法解方程;
(2)利用提公因式法解方程.
【详解】
解:(1),
,
,即,
,
;
(2),
,
,
或,
,.
【点睛】
本题考查的是一元二次方程的解法,解题的关键是掌握配方法、因式分解法解一元二次方程的一般步骤.
19.(1)20元;(2)不能达到1500元,理由见详解;(3)平均每天盈利最多1250元,达到最大值时应降价15元.
【解析】
【分析】
(1)设每件衬衫应降价元,则每件盈利元,每天可以售出,所以此时商场平均每天要盈利元,根据商场平均每天要盈利元,为等量关系列出方程求解即可.
(2)假设能达到,根据商场平均每天要盈利元,为等量关系列出方程,看该方程是否有解,有解则说明能达到,否则不能.
(3)设商场平均每天盈利元,由(1)可知商场平均每天盈利元与每件衬衫应降价元之间的函数关系为:,用“配方法”求出该函数的最大值,并求出降价多少.
【详解】
解:(1)设每件衬衫应降价元,则每件盈利元,每天可以售出,
由题意,得,
即:,
解,得,,
为了扩大销售量,增加盈利,尽快减少库存,所以的值应为20,
所以,若商场平均每天要盈利1200元,每件衬衫应降价20元;
(2)假设能达到,由题意,得,
整理,得,
,
即:该方程无解,
所以,商场平均每天盈利不能达到1500元;
(3)设商场平均每天盈利元,每件衬衫应降价元,
由题意,得,
,
,
,
当元时,该函数取得最大值为1250元,
所以,商场平均每天盈利最多1250元,达到最大值时应降价15元.
【点睛】
本题主要考查一元二次方程的应用,和二次函数的最值,关键在于理解清楚题意找出等量关系列出方程求解,另外还用到的知识点有“根的判别式”和用“配方法”求函数的最大值.
20.(1) a=﹣10;(2) 4-x的立方根是﹣5
【解析】
【分析】
(1)理解一个正数有几个平方根及其两个平方根间关系:一个正数有两个平方根,它们互为相反数,求出a的值;
根据a的值得出这个正数的两个平方根,即可得出这个正数,计算出44-x的值,再根据立方根的定义即可解答.
【详解】
解:(1)由题意得:3﹣a+2a+7=0,∴a=﹣10,
(2)由(1)可知x=169,则44-x=﹣125,
∴44-x的立方根是-5.
【点睛】
此题考查了立方根,平方根,注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
21.(1);(2); (3)估计该校最喜爱丙类图书的男生人数为人;女生人数为人.
【解析】
【分析】
(1)根据百分比=频数÷总数可得共调查的学生数;
(2)最喜爱丁类图书的学生数=总数减去喜欢甲、乙、丙三类图书的人数即可;再根据百分比=频数÷总数计算可得最喜爱甲类图书的人数所占百分比,扇形的圆心角的度数=百分比乘以360度即可得出.
(3)设男生人数为x人,则女生人数为1.2x人,由题意得方程x+1.2x=1500×20%,解出x的值可得答案.
【详解】
(1)共调查的学生数:40÷20%=200(人)
(2)最喜爱丁类图书的学生数:200 80 65 40=15(人);
最喜爱甲类图书的人数所占百分比:80÷200×100%=40%;
最喜爱甲类图书的人数扇形的圆心角的度数是:40%×=.
故答案为:
(3)设最喜爱丙类图书的男生人数为人,则女生人数为人.根据题意得
解得
当时,.
答:估计该校最喜爱丙类图书的男生人数为人;女生人数为人.
【点睛】
本题考查了条形统计图,用样本估计总体,扇形统计图,熟练掌握计算公式是解题的关键.
22.(1)小明家所在居民楼与大厦的距离CD的长度是40米;(2)太阳光不能直射到小明家.
【解析】
【分析】
(1)利用所给角的三角函数用CD表示出AD、BD;根据AB=AD+BD=74米,即可求得居民楼与大厦的距离.
(2)作FE∥AC,根据已知条件求出EB,再根据AE=AB﹣EB,求出AE,从而得出答案.
【详解】
解:(1)设CD=x米.
在Rt△ACD中,tan37°= ,
则
∴
在Rt△BCD中,
tan48°=,则
∴
∵AD+BD=AB,
∴
解得:x=40,
答:小明家所在居民楼与大厦的距离CD的长度是40米;
(2)作FE∥AC,由题意得:
解得:EB=25米,
∵AE=AB﹣EB=74﹣25=49米,
∴49>CF=44,
此时太阳光不能直射到小明家.
【点睛】
本题考查直角三角形的解法,首先构造直角三角形,再运用三角函数的定义解题.
23.(1)参见解析;(2)AO=BC且AO的延长线垂直BC.
【解析】
【分析】
(1)利用一组对边平行且相等的四边形是平行四边形的判定方法来四边形DGFE是平行四边形;(2)利用有一个角是直角的菱形是正方形找到OA应满足的条件.
【详解】
解:(1)由题意知:D,E分别是AB,AC的中点,
∴DE∥BC,DE=BC,又G,F分别是OB,OC的中点,
∴GF∥BC,GF=BC ,
∴DE∥GF,DE=GF,∴四边形DGFE是平行四边形.
(2)∵四边形DGFE是平行四边形,若四边形DGFE是正方形,则要满足有一组邻边相等,且有一个角是直角,
连接AO,因为DG平行且等于,GF平行且等于 ,
所以要想使DG=GF,则有= ,
即AO=BC;当∠EDG=90 ,
∵DG∥AO,
∴AO⊥DE,
∵DE∥BC,
∴AO的延长线垂直BC.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.新型冠状病毒疫情引起全国人民的关注,在社会各界贡献力量的同时,演艺圈也进行着公益接力.据有关报道称:截至2月16日20点,演艺圈人士共捐赠口罩近300万个,募集善款金额达到约577 000 000元.数据“577 000 000”用科学记数法表示为( )
A. B. C. D.
2.图中的内容是某同学完成的作业,嘉琪帮他做了批改,嘉琪批改正确的题数是( )
A.2个 B.3个 C.4个 D.5个
3.如图,梯形中,点在上,点是的中点,且若则的长为( )
A. B. C. D.
4.如图1是一座立交桥的示意图(道路宽度忽略不计),A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF;弯道为以点O为圆心的一段弧,且,,所对的圆心角为90o.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出,其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法正确的是( )
A.甲车在立交桥上共行驶9s
B.从F口出比从G口出多行驶40m
C.甲车从F口出,乙车从G口出
D.立交桥总长为120m
5.将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个正方形重叠形成的重叠部分的面积和为( )
A.cm2 B.cm2 C. cm2 D.()ncm2
6.分式方程的根是( )
A. B. C. D.
7.如图,长方形中有两个半圆和一个圆,已知长方形宽为,则阴影部分的面积为( )
A. B. C. D.
8.如图,在同一直线上,≌,,,则的值为( )
A. B. C. D.
9.如图,△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,若AD=2,AE=3,CE=1,则BD的长为( )
A.3 B.4 C.5 D.6
10.下面立体图形从前面看,所看见的图形是的是( )
A. B. C. D.
11.下面的计算正确的是( )
A. B. C. D.a6÷a2=a3
二、填空题
12.代数式的值为0,则x的值为__________.
13.已知关于x的一元二次方程ax2﹣2x﹣1=0有两个不相等的实数根,则a的取值范围是__________
14.的半径为1,弦上有一动点于点E,当点D从点C运动到点A时,则点E所经过的路径长为_________.
三、解答题
15.两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
16.画出下图中的图形绕点A顺时针旋转90°、180°、270°的图形.
17.阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
18.用适当的方法解方程:
(1);
(2).
19.某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元.为了扩大销售量,增加盈利,尽快减少库存,商场采取适当的降价措施.经调查发现,如果每件降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)该商场平均每天盈利能达到1500元吗?如果能,求出此时应降价多少;如果不能,请说明理由;
(3)该商场平均每天盈利最多多少元?达到最大值时应降价多少元?
20.正数x的两个平方根分别为3﹣a和2a+7.
(1)求a的值;
(2)求44﹣x这个数的立方根.
21.在武胜县中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生棵根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.
请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 人,表示最喜爱甲类图书的人数扇形的圆心角的度数是 ;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的倍,若这所学校共有学生人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
22.小明家所在居民楼的对面有一座大厦AB=74米,为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
(1)求小明家所在居民楼与大厦的距离CD的长度.(参考数据:sin37°≈,tan37°≈,sin48°≈,tan48°≈)
(2)冬季,在阳光的照射下测得一根1m长的竹竿在地面的影长是1.6m,试问此时太阳光是否能直射到小明家?请通过计算说明.
23.如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是正方形,请直接给出OA应满足的条件是 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于577 000 000有9位,所以可以确定n=9-1=8.
【详解】
577 000 000 =5.77×108.
故选:C.
【点睛】
此题考查科学记数法表示较大的数的方法,准确确定a与n值是关键.
2.B
【解析】
【分析】
分析各项计算得到结果,即可作出判断.
【详解】
①﹣1的倒数=﹣1,符合题意;
②1的平方根为±1,立方根等于本身,不符合题意;
③(﹣)2=,符合题意;
④|1﹣|=﹣1,符合题意;
⑤=﹣=﹣2,不符合题意,
故选:B.
【点睛】
此题主要考查对倒数、平方根、立方根以及绝对值的理解,熟练掌握,即可解题.
3.D
【解析】
【详解】
解:延长AF,交BC的延长线于G
∵AD∥BC
∴∠D=∠FCG
∵DF=FC,∠DFA=∠CFG
∴△ADF≌△GCF
∴CG=AD=2.7,FG=AF=4
∴AG=8
∵∠BAG=90°
∴
∵BE=AE
∴∠B=∠BAE
∵∠BAG=90°
∴∠B+∠G=90°,∠BAE+∠EAG=90°
∴∠G=∠EAG
∴EG=EA=EB
∴EG=5
∴EC=2.3
4.B
【解析】
【分析】
根据题意、结合图象问题可得.
【详解】
解:由图象可知,甲车驶出立交桥时,一共行驶的时间为3+2+3=8(s),故选项A不合题意;
根据两车运行路线,从F口驶出比从G口多走,弧长之和,用时为4s,则走40m,故选项B符合题意;
甲车先驶出立交桥,乙车后驶出立交桥,所以甲车从G口出,乙车从F口出,故选项C不合题意;
图中立交桥总长为:3×3×10+3×2×10=150(m),故选项D不合题意,
故选:B.
【点睛】
本题考查了动点问题的函数图象,理解题意、数形结合是解决问题的关键
5.B
【解析】
【分析】
根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n-1阴影部分的和.
【详解】
由题意可得阴影部分面积等于正方形面积的,即是,5个这样的正方形重叠部分(阴影部分)的面积和为×4,n个这样的正方形重叠部分(阴影部分)的面积和为×(n-1)=cm2.
故选B.
【点睛】
考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.
6.D
【解析】
【详解】
试题分析:方程的两边同乘,得:,解得.
检验:把代入.所以原方程的解为:.故选D.
考点:解分式方程.
7.C
【解析】
【分析】
如图,两个半圆和一个圆的直径都是相等为a,故可求出阴影部分的面积.
【详解】
解:由图形可知,
这两个半圆和一个圆的直径都相等是a,所以阴影部分的面积=2a2-2×圆的面积,
∴2a2-2×π×()2=2a2 =,
故选:C.
【点睛】
本题考查了列代数式问题,关键是得到阴影部分面积的等量关系.
8.C
【解析】
【分析】
设BD=x,根据全等的性质得到BC=x,故BE=AB=x+2,再根据得到方程即可求解.
【详解】
设BD=x
∵≌
∴BD=BC=x
∴BE=AB=x+2,
∵
∴AB+BD=8,即x+2+x=8
解得x=3
∴=EC×BD=×2×3=3
故选C.
【点睛】
此题主要考查全等的性质,解题的关键是熟知三角形的性质及三角形的面积公式.
9.B
【解析】
【详解】
∵AE=3,CE=1,
.
∵∠AED=∠B,∠A=∠A,
,
,
,
,
.
故选B.
10.C
【解析】
【详解】
根据题干分析可得:从前面看到的图形是 的是选项C中的图形,故选C.
11.C
【解析】
【分析】
根据幂的运算法则逐项计算即可.
【详解】
解:A. ,原选项不正确,不符合题意;
B. ,原选项不正确,不符合题意;
C. ,原选项正确,符合题意;
D. a6÷a2=a4,原选项不正确,不符合题意;
故选:C.
【点睛】
本题考查了幂的运算,解题关键是熟练运用幂的运算法则,准确进行计算.
12.2
【解析】
【分析】
根据分式值为0的条件:分子为0,分母不为0,列方程与不等式,求解即可.
【详解】
解:∵分式的值为零,
∴=0且,
=0
因式分解得
解方程得,;
解不等式得,或,
∴
故答案为:.
【点睛】
本题考查了分式值为零的条件,包含一元二次方程和一元一次不等式,解题关键是明确分式值为0,分子为0分母不为0,列出方程和不等式求解.
13.a>﹣1且a≠0
【解析】
【详解】
解∵关于的一元二次方程有两个不相等的实数根,
∴ ,解得:且.
即的取值范围是:且.
【点睛】
本题考查根据一元二次根的情况求参数.由本题题意可知字母的取值需同时满足2个条件:(1)由原方程是一元二次方程可知二次项系数;(2)由原方程有两个不相等的实数根可知,“根的判别式△的值大于0”.
14.或
【解析】
【分析】
利用定线AB所对得角是定角∠AEB=90°,可知点E得运动路径是以AB中点H为圆心,AH为半径的,注意求圆心角∠AHG的度数时分两种情况,AB,BC在圆心O的同侧或异侧.
【详解】
解:连接,,,过点作于点,
在中,,
动点的运动路径是以中点为圆心,为半径的,
分两种情况:
①,在圆心的同侧,
中,,
,,
在中,,
,
,得圆心角,
.
②,在圆心的异侧.
,得圆心角,
.
故答案为:或.
【点睛】
本题考查了90°的圆周角所对得弦是直径这一知识点得灵活运用,分类讨论的思想方法.
15.(1)△ACD≌△ABE,证明见解析;(2)线段DC和线段BE的关系是:垂直且相等,理由见解析.
【解析】
【分析】
(1)根据SAS证明△ACD≌△ABE 即可;
(2)线段DC和线段BE的关系是:垂直且相等.利用全等三角形的性质即可证明.
【详解】
解:(1)图2中的全等三角形是:△ACD≌△ABE.
证明:∵∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
∴∠BAE=∠CAD,
在△ABE与△ACD中,,
∴△ACD≌△ABE(SAS).
故答案为△ACD≌△ABE;
(2)线段DC和线段BE的关系是:垂直且相等.
理由:由(1)知:△ACD≌△ABE
∴DC=BE,∠ACD=∠B,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,即∠BCD=90°,
∴BE⊥DC,
∴线段DC和线段BE的关系是:垂直且相等.
【点睛】
本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
16.画图见解析.
【解析】
【分析】
根据旋转的特征,图形绕点A顺时针旋转90°、180°、270°,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可分别画出90°、180°、270°后的图形.
【详解】
画出图形绕点A顺时针旋转90°(红)、180°(绿)、270°(蓝)后的图形如图所示:
【点睛】
本题考查了旋转作图,旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.
17.(1)y=—2x+6,图象见详解:
(2)△的面积关于的函数表达式为
【解析】
【分析】
试题分析:(1)设直线l的函数表达式为y=k x+b,根据平行的性质可得k=—2,再根据直线l过点(1,4),即可求得直线l的函数表达式,最后根据描点法即可做出直线的图象;
(2)先分别求得直线l分别与y轴、x轴的交点A、B的坐标,再根据l∥,可设直线为y=—2x+t,从而表示出C点的坐标为(,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
【详解】
(1)设直线l的函数表达式为y=k x+b.
∵直线l与直线y=—2x—1平行,∴k=—2.
∵直线l过点(1,4),∴—2+b=4,∴b=6.
∴直线l的函数表达式为y=—2x+6,直线的图象如图:
(2)∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,6)、(3,0).
∵l∥,
∴直线为y=—2x+t.
∴C点的坐标为(,0).
∵t>0,
∴>0.
∴C点在x轴的正半轴上.
当C点在B点的左侧时,;
当C点在B点的右侧时,.
∴△的面积关于的函数表达式为
【点睛】
本题考查一次函数的综合题,本题知识点多,综合性强,难度较大,主要考查学生对一次函数的知识的熟练掌握情况.
18.(1);(2),
【解析】
【分析】
(1)利用配方法解方程;
(2)利用提公因式法解方程.
【详解】
解:(1),
,
,即,
,
;
(2),
,
,
或,
,.
【点睛】
本题考查的是一元二次方程的解法,解题的关键是掌握配方法、因式分解法解一元二次方程的一般步骤.
19.(1)20元;(2)不能达到1500元,理由见详解;(3)平均每天盈利最多1250元,达到最大值时应降价15元.
【解析】
【分析】
(1)设每件衬衫应降价元,则每件盈利元,每天可以售出,所以此时商场平均每天要盈利元,根据商场平均每天要盈利元,为等量关系列出方程求解即可.
(2)假设能达到,根据商场平均每天要盈利元,为等量关系列出方程,看该方程是否有解,有解则说明能达到,否则不能.
(3)设商场平均每天盈利元,由(1)可知商场平均每天盈利元与每件衬衫应降价元之间的函数关系为:,用“配方法”求出该函数的最大值,并求出降价多少.
【详解】
解:(1)设每件衬衫应降价元,则每件盈利元,每天可以售出,
由题意,得,
即:,
解,得,,
为了扩大销售量,增加盈利,尽快减少库存,所以的值应为20,
所以,若商场平均每天要盈利1200元,每件衬衫应降价20元;
(2)假设能达到,由题意,得,
整理,得,
,
即:该方程无解,
所以,商场平均每天盈利不能达到1500元;
(3)设商场平均每天盈利元,每件衬衫应降价元,
由题意,得,
,
,
,
当元时,该函数取得最大值为1250元,
所以,商场平均每天盈利最多1250元,达到最大值时应降价15元.
【点睛】
本题主要考查一元二次方程的应用,和二次函数的最值,关键在于理解清楚题意找出等量关系列出方程求解,另外还用到的知识点有“根的判别式”和用“配方法”求函数的最大值.
20.(1) a=﹣10;(2) 4-x的立方根是﹣5
【解析】
【分析】
(1)理解一个正数有几个平方根及其两个平方根间关系:一个正数有两个平方根,它们互为相反数,求出a的值;
根据a的值得出这个正数的两个平方根,即可得出这个正数,计算出44-x的值,再根据立方根的定义即可解答.
【详解】
解:(1)由题意得:3﹣a+2a+7=0,∴a=﹣10,
(2)由(1)可知x=169,则44-x=﹣125,
∴44-x的立方根是-5.
【点睛】
此题考查了立方根,平方根,注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
21.(1);(2); (3)估计该校最喜爱丙类图书的男生人数为人;女生人数为人.
【解析】
【分析】
(1)根据百分比=频数÷总数可得共调查的学生数;
(2)最喜爱丁类图书的学生数=总数减去喜欢甲、乙、丙三类图书的人数即可;再根据百分比=频数÷总数计算可得最喜爱甲类图书的人数所占百分比,扇形的圆心角的度数=百分比乘以360度即可得出.
(3)设男生人数为x人,则女生人数为1.2x人,由题意得方程x+1.2x=1500×20%,解出x的值可得答案.
【详解】
(1)共调查的学生数:40÷20%=200(人)
(2)最喜爱丁类图书的学生数:200 80 65 40=15(人);
最喜爱甲类图书的人数所占百分比:80÷200×100%=40%;
最喜爱甲类图书的人数扇形的圆心角的度数是:40%×=.
故答案为:
(3)设最喜爱丙类图书的男生人数为人,则女生人数为人.根据题意得
解得
当时,.
答:估计该校最喜爱丙类图书的男生人数为人;女生人数为人.
【点睛】
本题考查了条形统计图,用样本估计总体,扇形统计图,熟练掌握计算公式是解题的关键.
22.(1)小明家所在居民楼与大厦的距离CD的长度是40米;(2)太阳光不能直射到小明家.
【解析】
【分析】
(1)利用所给角的三角函数用CD表示出AD、BD;根据AB=AD+BD=74米,即可求得居民楼与大厦的距离.
(2)作FE∥AC,根据已知条件求出EB,再根据AE=AB﹣EB,求出AE,从而得出答案.
【详解】
解:(1)设CD=x米.
在Rt△ACD中,tan37°= ,
则
∴
在Rt△BCD中,
tan48°=,则
∴
∵AD+BD=AB,
∴
解得:x=40,
答:小明家所在居民楼与大厦的距离CD的长度是40米;
(2)作FE∥AC,由题意得:
解得:EB=25米,
∵AE=AB﹣EB=74﹣25=49米,
∴49>CF=44,
此时太阳光不能直射到小明家.
【点睛】
本题考查直角三角形的解法,首先构造直角三角形,再运用三角函数的定义解题.
23.(1)参见解析;(2)AO=BC且AO的延长线垂直BC.
【解析】
【分析】
(1)利用一组对边平行且相等的四边形是平行四边形的判定方法来四边形DGFE是平行四边形;(2)利用有一个角是直角的菱形是正方形找到OA应满足的条件.
【详解】
解:(1)由题意知:D,E分别是AB,AC的中点,
∴DE∥BC,DE=BC,又G,F分别是OB,OC的中点,
∴GF∥BC,GF=BC ,
∴DE∥GF,DE=GF,∴四边形DGFE是平行四边形.
(2)∵四边形DGFE是平行四边形,若四边形DGFE是正方形,则要满足有一组邻边相等,且有一个角是直角,
连接AO,因为DG平行且等于,GF平行且等于 ,
所以要想使DG=GF,则有= ,
即AO=BC;当∠EDG=90 ,
∵DG∥AO,
∴AO⊥DE,
∵DE∥BC,
∴AO的延长线垂直BC.
答案第1页,共2页
答案第1页,共2页
同课章节目录
