华东师大版七年级下册数学 10.3.1 图形的旋转 课件(共21张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.3.1 图形的旋转 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 974.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
*
动动脑筋:以上这些旋转图片有什么共同的特征?
生活中的旋转
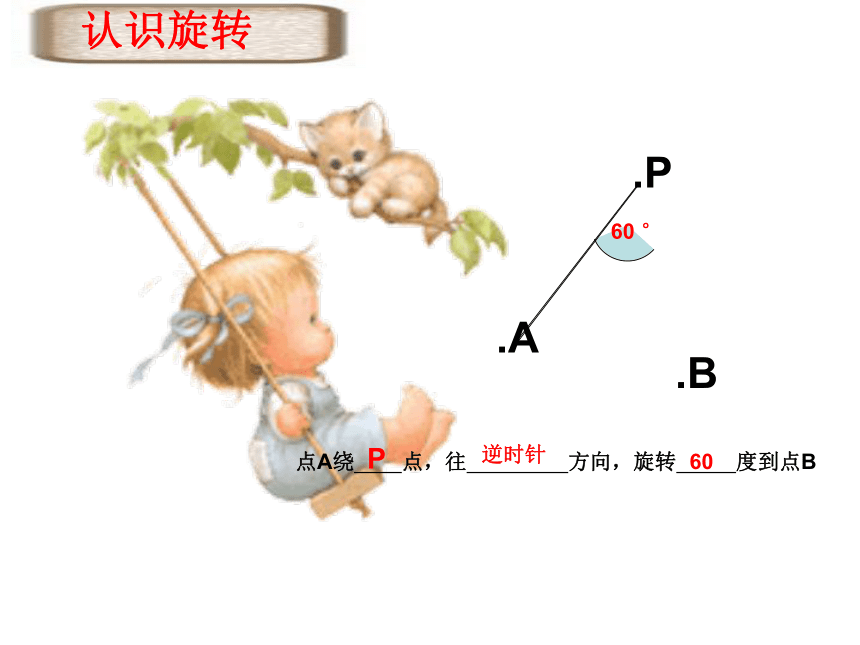
认识旋转
.P
.A
.B
60 °
点A绕 点,往 方向,旋转 度到点B
P
逆时针
60
O
90°
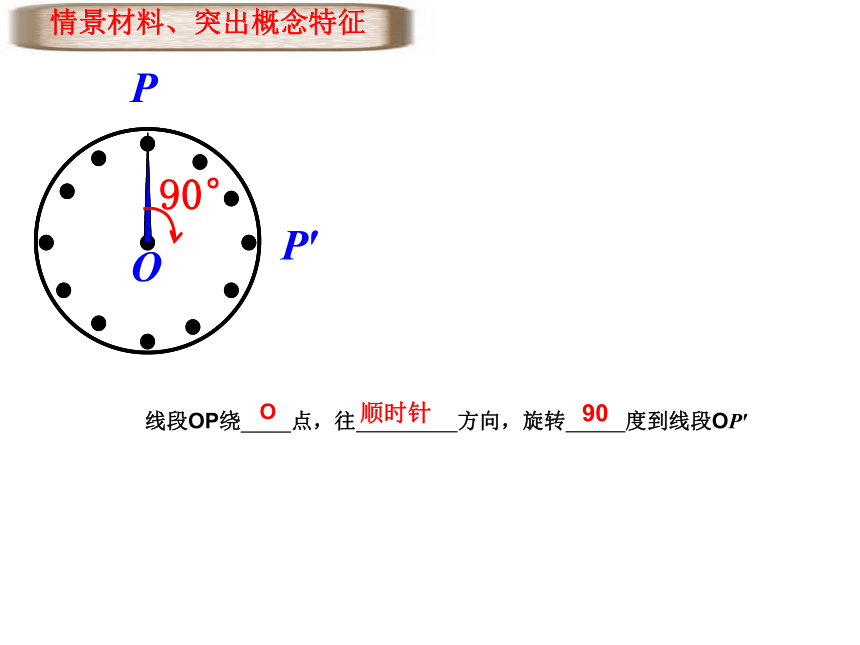
情景材料、突出概念特征
P′
P
O
线段OP绕 点,往 方向,旋转 度到线段OP′
顺时针
90
旋转的定义:
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
这个点称为旋转中心
转动的角称为旋转角
旋转三要素
一个定点
一个方向
一个角度
你能给旋转一个定义吗?
(旋转中心)
(旋转方向)
(旋转角)
1.下列现象中,属于旋转的有( )个
①地下水位逐年下降;②方向盘的转动;③传送带的移动;④水龙头开关的转动;⑤钟摆的运动; ⑥荡秋千运动.
A.2 B.3 C.4 D.5
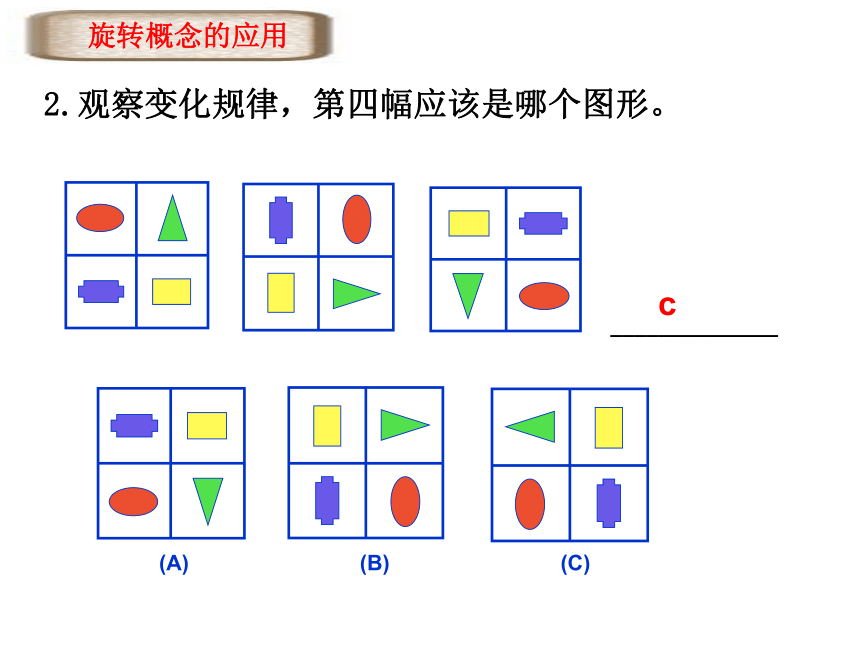
旋转概念的应用
C
______________
(A)
(B)
(C)
2.观察变化规律,第四幅应该是哪个图形。
旋转概念的应用
c
A
B
O
A′
B′
旋转性质
活动准备:一个直角三角板
活动形式:小组合作
活动步骤:
①在纸片上画出直角三角形的形状;
②使其绕着一个顶点旋转一定的角度,再画出此时的三角形。
活动目标:
①旋转前后的三角形形状大小变化了吗?
②找出对应点,它们到旋转中心距离相等吗?
③哪些角是旋转角?它们的数量关系怎样? ④对应边、对应角又怎样的关系?
活动1
我的发现:
1、旋转前后图形的形状和大小不变;
2、OA=OA′,OB=OB′,对应点到旋转中心的距离相等
3、∠AOA′= ∠BOB′,旋转的角度相等
4、 OA=OA′,OB=OB′,AB=A′B′, ∠A= ∠A′,∠B=∠ B′对应边相等,对应角相等
E
D
A
B
F
C
O
旋转性质
(自动演示)
活动2
1、找出对应点:
A的对应点是 ( ),B的对应点是( ),C的对应点是( )
2、观察两个三角形你能得到哪些相等的线段和相等的角?
3、连结OA、OB、OC、OD、OE、OF,你又能发现哪些相等的线段和相等的角?AO=( ) ,BO=( ),CO=( )
( )
D
E
DO
EO
FO
F
∠COF=∠BOE=∠AOD
你能否观察、发现旋转有哪些性质?
1、旋转不改变图形的形状和大小
(旋转后的图形与原图形全等)
2、旋转图形的任意一对对应点到旋转中心的距离相等
3、旋转图形的任意一对对应点与旋转中心的连线所
成的角都相等,都是旋转角
4、对应线段相等,对应角相等
“四特点”
注:每组对应点与旋转中心连线所成的角叫做旋转角
旋转的性质
3、如图所示的是△ OAB绕点O,按顺时针旋转一定角度得
到△ OCD,则
O
A
B
C
D
旋转中心是( )
旋转的角可以表示为( )
点B的对应点是( )
线段AB的对应线段是( )
∠A的对应角是( )
∠B的对应角是( )
旋转性质的应用
点o
点D
线段CD
∠AOC、∠BOD
∠C
∠D
4、如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,已知AB=4 cm,∠A=30 , ∠ABO=75 ,∠A′OB=40 .
则A′B′的长是_____ cm
∠A′=______
∠AOB =______
旋转角可以用哪些角表示?
_________________________
等于______度
旋转性质的应用
4
30
35
75
∠AOA′、∠BOB′
5、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
A点
60°
AC的中点
旋转图形的形成
1、下图是中华人民共和国香港特别行政区区徽是由
为基本图形绕 点按 时针方向旋转 次,分别旋
转 前后的图形共同形成的。
5
一个紫荆花瓣
中心
72°、144 °、216 °、288 °、360 °
顺或逆
“五说明”
基本图形、旋转中心、旋转方向、旋转次数、旋转角度
如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
知识拓展、延伸
旋转的性质:“四特点”
1、旋转不改变图形的形状和大小。
2、对应点到旋转中心的距离相等。
3、每组对应点与旋转中心的连线所成的角均相等,且等于旋转角。
4、对应线段相等,对应角相等
旋转的定义: “三要素”
一个定点、一个方向、一个角度
旋转图形的形成:“五说明”
基本图形、旋转中心、旋转方向、旋转次数、旋转角度
课堂小结
课后作业
1、思考:如图,边长为4的正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,则重合部分的面积为( )
2、以一直角三角形为“基本图形”,通过多次旋转得到一个风车或
风轮图案,你能设计出几种风车风轮图案呢?请你设计一个图案,
小组共同完成。
拓展课程内容,着眼数学应用
其实生活亦然,当你感到蓝瘦香菇的时候,不妨旋转一个角度去看世界,相信你会有一个柳暗花明的美好心情。
祝同学们每天都开心快乐!
寄语同学
*
动动脑筋:以上这些旋转图片有什么共同的特征?
生活中的旋转
认识旋转
.P
.A
.B
60 °
点A绕 点,往 方向,旋转 度到点B
P
逆时针
60
O
90°
情景材料、突出概念特征
P′
P
O
线段OP绕 点,往 方向,旋转 度到线段OP′
顺时针
90
旋转的定义:
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
这个点称为旋转中心
转动的角称为旋转角
旋转三要素
一个定点
一个方向
一个角度
你能给旋转一个定义吗?
(旋转中心)
(旋转方向)
(旋转角)
1.下列现象中,属于旋转的有( )个
①地下水位逐年下降;②方向盘的转动;③传送带的移动;④水龙头开关的转动;⑤钟摆的运动; ⑥荡秋千运动.
A.2 B.3 C.4 D.5
旋转概念的应用
C
______________
(A)
(B)
(C)
2.观察变化规律,第四幅应该是哪个图形。
旋转概念的应用
c
A
B
O
A′
B′
旋转性质
活动准备:一个直角三角板
活动形式:小组合作
活动步骤:
①在纸片上画出直角三角形的形状;
②使其绕着一个顶点旋转一定的角度,再画出此时的三角形。
活动目标:
①旋转前后的三角形形状大小变化了吗?
②找出对应点,它们到旋转中心距离相等吗?
③哪些角是旋转角?它们的数量关系怎样? ④对应边、对应角又怎样的关系?
活动1
我的发现:
1、旋转前后图形的形状和大小不变;
2、OA=OA′,OB=OB′,对应点到旋转中心的距离相等
3、∠AOA′= ∠BOB′,旋转的角度相等
4、 OA=OA′,OB=OB′,AB=A′B′, ∠A= ∠A′,∠B=∠ B′对应边相等,对应角相等
E
D
A
B
F
C
O
旋转性质
(自动演示)
活动2
1、找出对应点:
A的对应点是 ( ),B的对应点是( ),C的对应点是( )
2、观察两个三角形你能得到哪些相等的线段和相等的角?
3、连结OA、OB、OC、OD、OE、OF,你又能发现哪些相等的线段和相等的角?AO=( ) ,BO=( ),CO=( )
( )
D
E
DO
EO
FO
F
∠COF=∠BOE=∠AOD
你能否观察、发现旋转有哪些性质?
1、旋转不改变图形的形状和大小
(旋转后的图形与原图形全等)
2、旋转图形的任意一对对应点到旋转中心的距离相等
3、旋转图形的任意一对对应点与旋转中心的连线所
成的角都相等,都是旋转角
4、对应线段相等,对应角相等
“四特点”
注:每组对应点与旋转中心连线所成的角叫做旋转角
旋转的性质
3、如图所示的是△ OAB绕点O,按顺时针旋转一定角度得
到△ OCD,则
O
A
B
C
D
旋转中心是( )
旋转的角可以表示为( )
点B的对应点是( )
线段AB的对应线段是( )
∠A的对应角是( )
∠B的对应角是( )
旋转性质的应用
点o
点D
线段CD
∠AOC、∠BOD
∠C
∠D
4、如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,已知AB=4 cm,∠A=30 , ∠ABO=75 ,∠A′OB=40 .
则A′B′的长是_____ cm
∠A′=______
∠AOB =______
旋转角可以用哪些角表示?
_________________________
等于______度
旋转性质的应用
4
30
35
75
∠AOA′、∠BOB′
5、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
A点
60°
AC的中点
旋转图形的形成
1、下图是中华人民共和国香港特别行政区区徽是由
为基本图形绕 点按 时针方向旋转 次,分别旋
转 前后的图形共同形成的。
5
一个紫荆花瓣
中心
72°、144 °、216 °、288 °、360 °
顺或逆
“五说明”
基本图形、旋转中心、旋转方向、旋转次数、旋转角度
如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
知识拓展、延伸
旋转的性质:“四特点”
1、旋转不改变图形的形状和大小。
2、对应点到旋转中心的距离相等。
3、每组对应点与旋转中心的连线所成的角均相等,且等于旋转角。
4、对应线段相等,对应角相等
旋转的定义: “三要素”
一个定点、一个方向、一个角度
旋转图形的形成:“五说明”
基本图形、旋转中心、旋转方向、旋转次数、旋转角度
课堂小结
课后作业
1、思考:如图,边长为4的正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,则重合部分的面积为( )
2、以一直角三角形为“基本图形”,通过多次旋转得到一个风车或
风轮图案,你能设计出几种风车风轮图案呢?请你设计一个图案,
小组共同完成。
拓展课程内容,着眼数学应用
其实生活亦然,当你感到蓝瘦香菇的时候,不妨旋转一个角度去看世界,相信你会有一个柳暗花明的美好心情。
祝同学们每天都开心快乐!
寄语同学
