华东师大版八年级下册数学 19.2.2 菱形的判定 课件(共19张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.2.2 菱形的判定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 150.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
菱形的判定
A
B
C
D
O
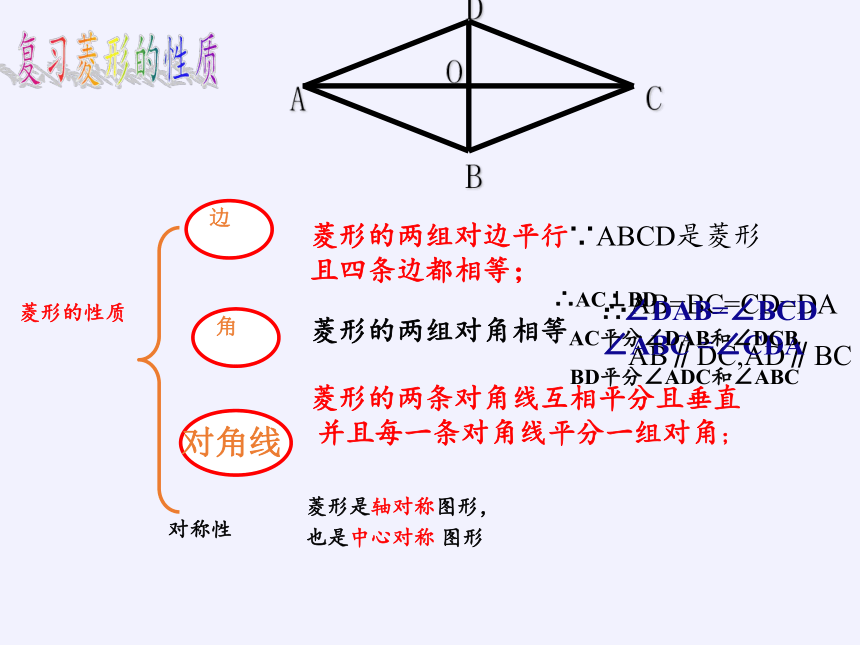
菱形的两条对角线互相平分且垂直
并且每一条对角线平分一组对角;
复习菱形的性质
菱形是轴对称图形,
也是中心对称 图形
菱形的性质
边
角
对角线
菱形的两组对角相等
对称性
∵ABCD是菱形
∴AB=BC=CD=DA
AB∥DC,AD∥BC
菱形的两组对边平行
且四条边都相等;
∴∠DAB=∠BCD ∠ABC =∠CDA
∴AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
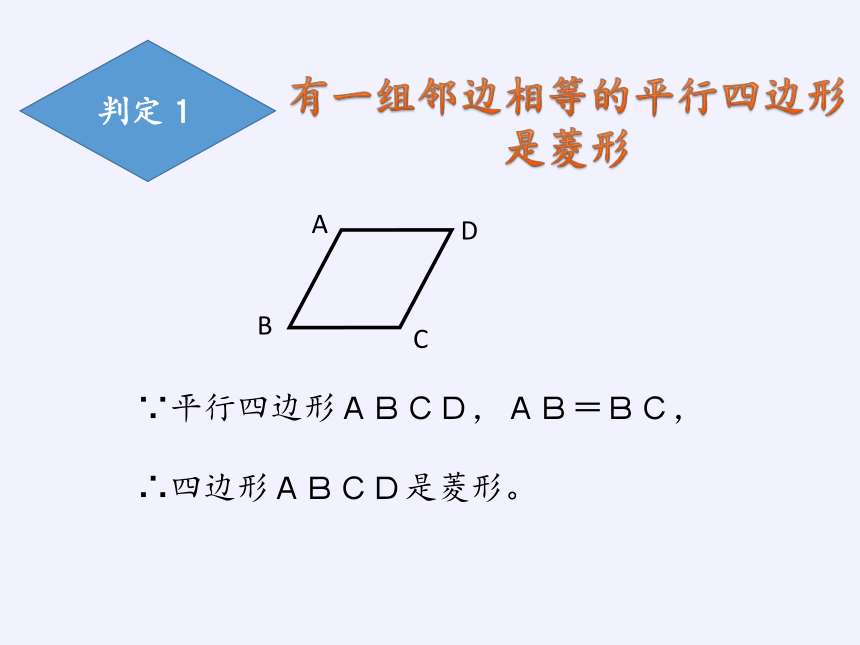
判定1
有一组邻边相等的平行四边形
是菱形
A
B
C
D
∵平行四边形ABCD,AB=BC,
∴四边形ABCD是菱形。
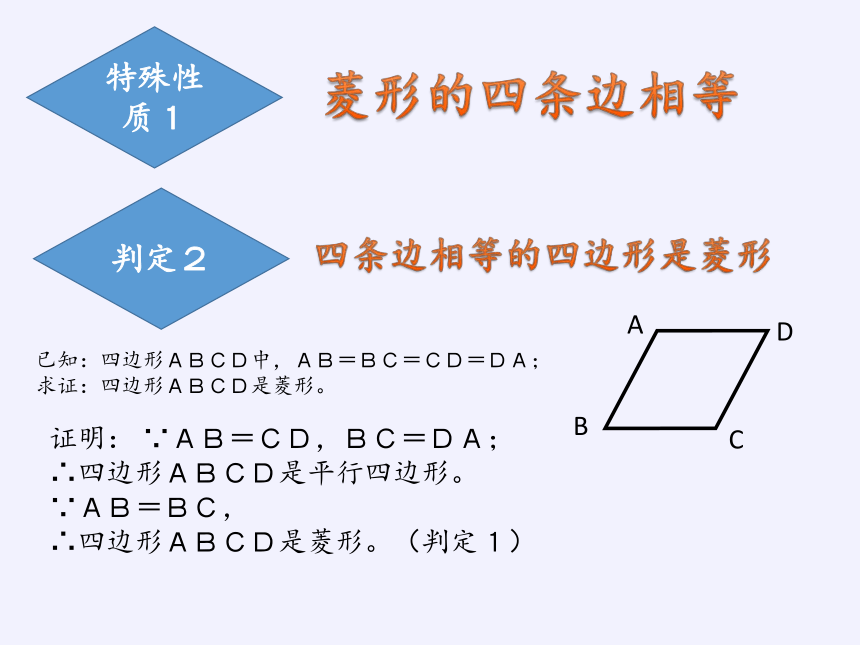
特殊性质1
菱形的四条边相等
判定2
四条边相等的四边形是菱形
A
B
C
D
已知:四边形ABCD中,AB=BC=CD=DA;
求证:四边形ABCD是菱形。
证明: ∵AB=CD,BC=DA;
∴四边形ABCD是平行四边形。
∵AB=BC,
∴四边形ABCD是菱形。(判定1)
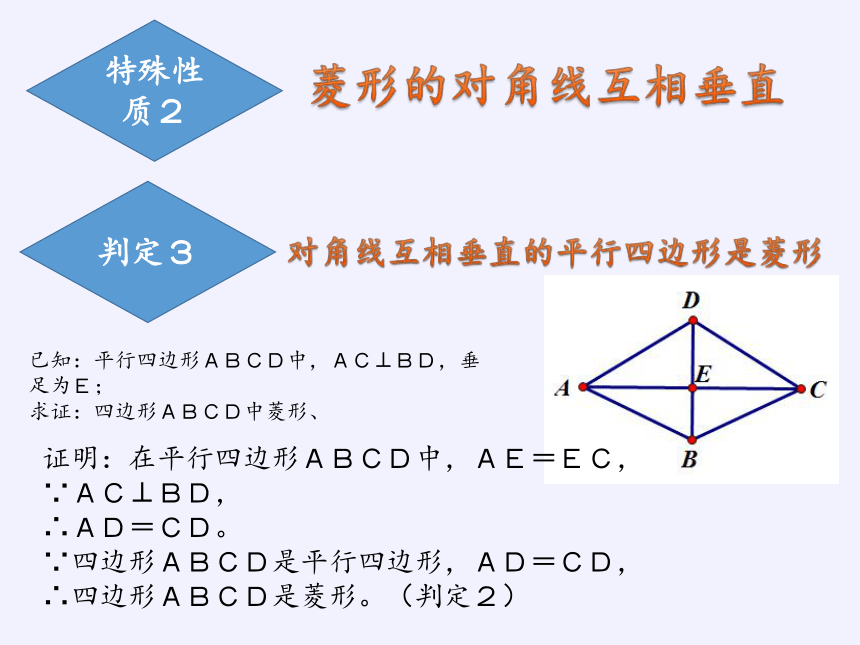
特殊性质2
菱形的对角线互相垂直
判定3
对角线互相垂直的平行四边形是菱形
已知:平行四边形ABCD中,AC⊥BD,垂足为E;
求证:四边形ABCD中菱形、
证明:在平行四边形ABCD中,AE=EC,
∵AC⊥BD,
∴AD=CD。
∵四边形ABCD是平行四边形,AD=CD,
∴四边形ABCD是菱形。(判定2)
归纳菱形的判定
1、有一组邻边相等的平行四边形是菱形
2、四条边相等的四边形是菱形
3、对角线互相垂直的平行四边形是菱形
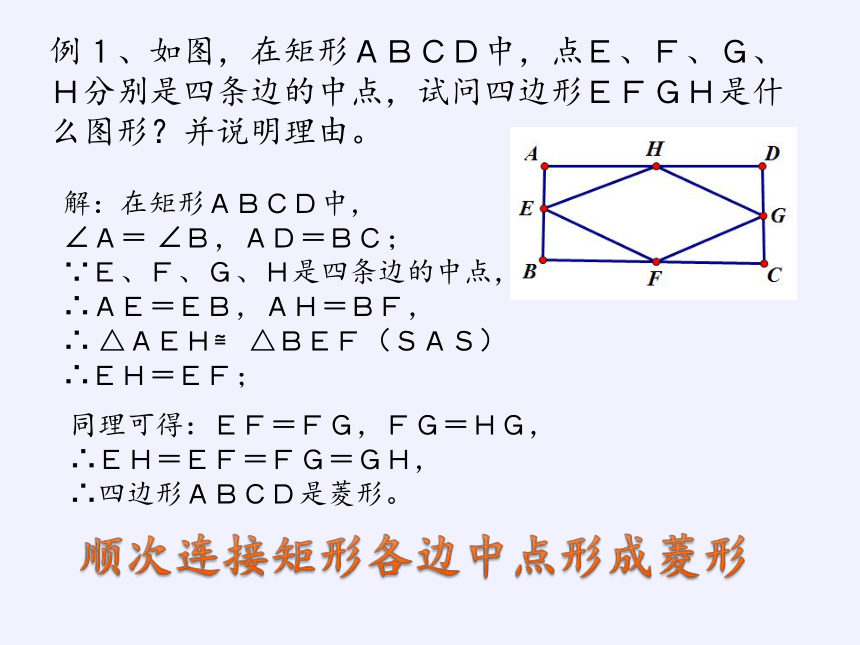
例1、如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由。
解:在矩形ABCD中,
∠A= ∠B,AD=BC;
∵E、F、G、H是四条边的中点,
∴AE=EB,AH=BF,
∴ △AEH≌ △BEF(SAS)
∴EH=EF;
同理可得:EF=FG,FG=HG,
∴EH=EF=FG=GH,
∴四边形ABCD是菱形。
顺次连接矩形各边中点形成菱形
例2、如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F。
求证:四边形AECF的菱形。
证明:在矩形ABCD中,
∵AD∥BC,
∴ ∠DAC= ∠BCA, ∠AEF= ∠CFE
又∵EF平分AC,
∴OA=OC,
△AOE≌ △COF(AAS)
∴OE=OF。
∵OA=OC,OE=OF,
∴四边形ABCD是平行四边形。
∵平行四边形ABCD中,AC⊥EF,
∴四边形ABCD是菱形。(判定3)
例3、试说明菱形的面积等于两条对角线的乘积的一半。
已知:菱形ABCD,AC和BD是对角线,交于点E。
求证:S菱形ABCD=
证明:在菱形ABCD中,
∵AC⊥BD,BE=DE,
∴S菱形ABCD=S△ABC+S△ADC
=
菱形的面积等于对角线乘积的一半
例4、如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.
C
F
G
B
D
A
E
∵ ∠3= 90°-∠1, ∠4= 90°-∠2,
∴ CE=CF
(等腰三角形的定义)
∴ ∠3= ∠4
C
F
G
B
D
A
E
1
2
3
4
∵ AF是∠BAC的平分线,
(角平分线的定义)
∴ ∠1= ∠2
∵ FC⊥AC, FG⊥AB, AF是∠BAC的平分线,
∴ FC=FG
(角平分线的性质)
∵ FG⊥AB, CD⊥AB,
∴ CD∥FG
(垂直于同一条直线的两条直线平行)
证明:
∴ EC=FG
(等量代换)
1、下列条件中,能判定一个四边形为菱形的条件是( )
A、对角线互相平分的四边形
B、对角线互相垂直且平分的四边形
C、对角线相等的四边形
D、对角线相等且互相垂直的四边形
B
A
O
D
C
B
练一练
2、下列三个图形都是菱形吗 为什么?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
3
3
4
4
┍
练一练
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
矩
菱
矩
菱
4、如图, 平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=8,DB=6;
求证:四边形ABCD是菱形.
A
B
C
D
O
5、已知:如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
∟
6、如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
A
B
F
N
D
M
E
C
A
B
C
D
O
E
7.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
谢 谢
菱形的判定
A
B
C
D
O
菱形的两条对角线互相平分且垂直
并且每一条对角线平分一组对角;
复习菱形的性质
菱形是轴对称图形,
也是中心对称 图形
菱形的性质
边
角
对角线
菱形的两组对角相等
对称性
∵ABCD是菱形
∴AB=BC=CD=DA
AB∥DC,AD∥BC
菱形的两组对边平行
且四条边都相等;
∴∠DAB=∠BCD ∠ABC =∠CDA
∴AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
判定1
有一组邻边相等的平行四边形
是菱形
A
B
C
D
∵平行四边形ABCD,AB=BC,
∴四边形ABCD是菱形。
特殊性质1
菱形的四条边相等
判定2
四条边相等的四边形是菱形
A
B
C
D
已知:四边形ABCD中,AB=BC=CD=DA;
求证:四边形ABCD是菱形。
证明: ∵AB=CD,BC=DA;
∴四边形ABCD是平行四边形。
∵AB=BC,
∴四边形ABCD是菱形。(判定1)
特殊性质2
菱形的对角线互相垂直
判定3
对角线互相垂直的平行四边形是菱形
已知:平行四边形ABCD中,AC⊥BD,垂足为E;
求证:四边形ABCD中菱形、
证明:在平行四边形ABCD中,AE=EC,
∵AC⊥BD,
∴AD=CD。
∵四边形ABCD是平行四边形,AD=CD,
∴四边形ABCD是菱形。(判定2)
归纳菱形的判定
1、有一组邻边相等的平行四边形是菱形
2、四条边相等的四边形是菱形
3、对角线互相垂直的平行四边形是菱形
例1、如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由。
解:在矩形ABCD中,
∠A= ∠B,AD=BC;
∵E、F、G、H是四条边的中点,
∴AE=EB,AH=BF,
∴ △AEH≌ △BEF(SAS)
∴EH=EF;
同理可得:EF=FG,FG=HG,
∴EH=EF=FG=GH,
∴四边形ABCD是菱形。
顺次连接矩形各边中点形成菱形
例2、如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F。
求证:四边形AECF的菱形。
证明:在矩形ABCD中,
∵AD∥BC,
∴ ∠DAC= ∠BCA, ∠AEF= ∠CFE
又∵EF平分AC,
∴OA=OC,
△AOE≌ △COF(AAS)
∴OE=OF。
∵OA=OC,OE=OF,
∴四边形ABCD是平行四边形。
∵平行四边形ABCD中,AC⊥EF,
∴四边形ABCD是菱形。(判定3)
例3、试说明菱形的面积等于两条对角线的乘积的一半。
已知:菱形ABCD,AC和BD是对角线,交于点E。
求证:S菱形ABCD=
证明:在菱形ABCD中,
∵AC⊥BD,BE=DE,
∴S菱形ABCD=S△ABC+S△ADC
=
菱形的面积等于对角线乘积的一半
例4、如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.
求证:四边形EGFC为菱形.
C
F
G
B
D
A
E
∵ ∠3= 90°-∠1, ∠4= 90°-∠2,
∴ CE=CF
(等腰三角形的定义)
∴ ∠3= ∠4
C
F
G
B
D
A
E
1
2
3
4
∵ AF是∠BAC的平分线,
(角平分线的定义)
∴ ∠1= ∠2
∵ FC⊥AC, FG⊥AB, AF是∠BAC的平分线,
∴ FC=FG
(角平分线的性质)
∵ FG⊥AB, CD⊥AB,
∴ CD∥FG
(垂直于同一条直线的两条直线平行)
证明:
∴ EC=FG
(等量代换)
1、下列条件中,能判定一个四边形为菱形的条件是( )
A、对角线互相平分的四边形
B、对角线互相垂直且平分的四边形
C、对角线相等的四边形
D、对角线相等且互相垂直的四边形
B
A
O
D
C
B
练一练
2、下列三个图形都是菱形吗 为什么?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
3
3
4
4
┍
练一练
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
矩
菱
矩
菱
4、如图, 平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=8,DB=6;
求证:四边形ABCD是菱形.
A
B
C
D
O
5、已知:如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
∟
6、如图,已知在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.
A
B
F
N
D
M
E
C
A
B
C
D
O
E
7.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
谢 谢
