华东师大版八年级下册数学 17.4.2 反比例函数的图象和性质(3) 教案(表格式)
文档属性
| 名称 | 华东师大版八年级下册数学 17.4.2 反比例函数的图象和性质(3) 教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 07:38:38 | ||
图片预览



文档简介
反比例函数中K几何意义
教学目标 知识与技能 了解反比例函数中k的值与相应矩形、三角形面积之间的关系。 能灵活运用反比例函数中k的几何意义解决相关问题。
过程与反法 利用几何画板让学生自己尝试在反比例函数图像上任取一点p,过点p向x轴y轴作垂线。从而探究出两垂线与坐标轴形成的矩形、三角形面积与k的关系。
情感态度与价值观 通过学生自主探索反比例函数中k的几何意义,训练学生的探索能力、语言组织能力和分析问题解决问题的能力。培养学生转化及数形结合的数学思想方法。
重点 探索反比例函数中反比例系数k的几何意义
难点 灵活运用反比例函数中k的几何意义解决问题
活动流程图 活动内容和目的
活动1 提出问题 探索关系 活动2 提出问题 探索关系 活动3 解决问题 综合运用 活动4 拓展提升 活动5 归纳小结 通过几何画板帮助学生探索反比例函数中k与矩形面积的关系。 通过几何画板帮助学生探索反比例函数中k与三角形面积的关系。 检测学生对知识的理解运用情况 发散学生的思维能力,鼓励学生有敢说、敢讲的勇气。 师生共同归纳小结
问题与情景 师生行为 设计意图
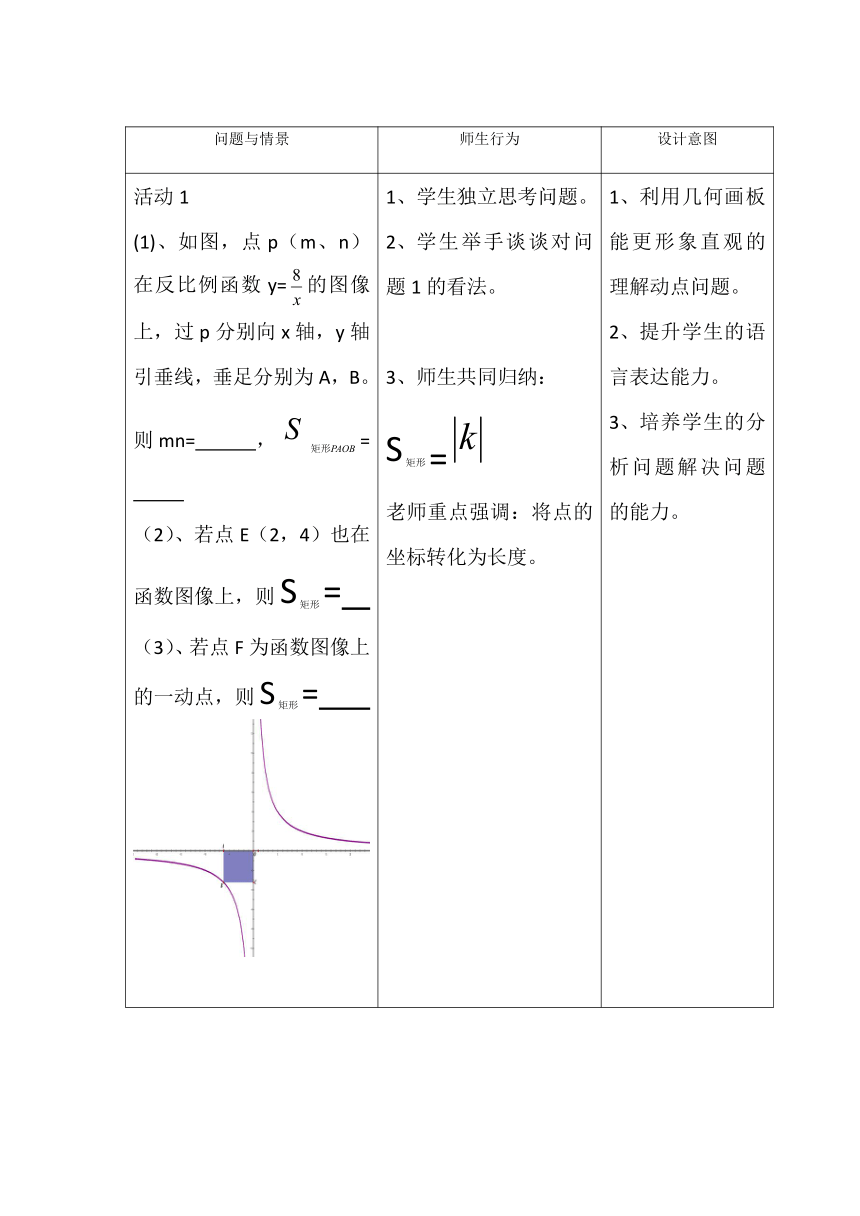
活动1 (1)、如图,点p(m、n)在反比例函数y=的图像上,过p分别向x轴,y轴引垂线,垂足分别为A,B。则mn= ,= (2)、若点E(2,4)也在函数图像上,则S= (3)、若点F为函数图像上的一动点,则S= 学生独立思考问题。 学生举手谈谈对问题1的看法。 师生共同归纳: S= 老师重点强调:将点的坐标转化为长度。 利用几何画板能更形象直观的理解动点问题。 提升学生的语言表达能力。 培养学生的分析问题解决问题的能力。
活动2: 如图,点E(m,n)在反比例函数y=的图像上,过点p向x轴作垂线,垂足为F,则S= 若图像上有一动点F,则S= 学生独立思考并谈谈自己的想法。 师生共同归纳: S= 3、学生前后4人交流讨论对矩形,三角形面积与k的关系的理解。 在此活动中,老师重点关注:学生有没有将点的坐标转化为长度的意识。面积与k的绝对值相关。 利用几何画板更形象直观的理解动点问题。 学生间交流自己的理解能加深对知识的理解或发现自己在理解上存在的问题。
练习: 如图所示,A是反比例函数图像上一点,过点A作ABy轴于点B,点P在x轴上,的面积为2,求反比例函数的解析式。 活动三: 拓展提升 双曲线y,y在第一象限的图像如图所示,点A在双曲线y=上,且AB//x轴,S=1,求y的函数关系式。 2、如图,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-和y=的图像交于A和B,若点C是x轴上任一点,连接AC,BC,求ABC的面积。 活动4:小结 同学们说说这节课你有哪些收获? 给学生足够的时间思考。 让学生谈谈自己的想法,其他同学补充。 师生共同完善该题,由学生归纳总结。 1、让学生有足够的时间思考。 老师作适当的引导,鼓励有想法的同学到讲台上去说出自己的解法。 师生共同完善该题的解题方法与步骤。 反思、归纳、总结。 若时间充足该题可以作为一道练习题。引导学生思考是否还存在AB//y轴的可能?三角形面积又如何求呢?同学们可以自己出出题,同学间交流讨论。 让尽量多的同学谈谈自己的收获 1、利用 几何画板学生能直观的观察到两三角形同底等高,面积相等。 2、培养学生养成善于反思、归纳、总结的习惯。 锻炼学生的表达能力和展现自我的勇气。例题的设置可以发散学生的思维。 分层教学,让基础好的同学有更多的收获,激发学生学习数学的兴趣,让他们体会成功的喜悦。 培养自己归纳总结的习惯
教学目标 知识与技能 了解反比例函数中k的值与相应矩形、三角形面积之间的关系。 能灵活运用反比例函数中k的几何意义解决相关问题。
过程与反法 利用几何画板让学生自己尝试在反比例函数图像上任取一点p,过点p向x轴y轴作垂线。从而探究出两垂线与坐标轴形成的矩形、三角形面积与k的关系。
情感态度与价值观 通过学生自主探索反比例函数中k的几何意义,训练学生的探索能力、语言组织能力和分析问题解决问题的能力。培养学生转化及数形结合的数学思想方法。
重点 探索反比例函数中反比例系数k的几何意义
难点 灵活运用反比例函数中k的几何意义解决问题
活动流程图 活动内容和目的
活动1 提出问题 探索关系 活动2 提出问题 探索关系 活动3 解决问题 综合运用 活动4 拓展提升 活动5 归纳小结 通过几何画板帮助学生探索反比例函数中k与矩形面积的关系。 通过几何画板帮助学生探索反比例函数中k与三角形面积的关系。 检测学生对知识的理解运用情况 发散学生的思维能力,鼓励学生有敢说、敢讲的勇气。 师生共同归纳小结
问题与情景 师生行为 设计意图
活动1 (1)、如图,点p(m、n)在反比例函数y=的图像上,过p分别向x轴,y轴引垂线,垂足分别为A,B。则mn= ,= (2)、若点E(2,4)也在函数图像上,则S= (3)、若点F为函数图像上的一动点,则S= 学生独立思考问题。 学生举手谈谈对问题1的看法。 师生共同归纳: S= 老师重点强调:将点的坐标转化为长度。 利用几何画板能更形象直观的理解动点问题。 提升学生的语言表达能力。 培养学生的分析问题解决问题的能力。
活动2: 如图,点E(m,n)在反比例函数y=的图像上,过点p向x轴作垂线,垂足为F,则S= 若图像上有一动点F,则S= 学生独立思考并谈谈自己的想法。 师生共同归纳: S= 3、学生前后4人交流讨论对矩形,三角形面积与k的关系的理解。 在此活动中,老师重点关注:学生有没有将点的坐标转化为长度的意识。面积与k的绝对值相关。 利用几何画板更形象直观的理解动点问题。 学生间交流自己的理解能加深对知识的理解或发现自己在理解上存在的问题。
练习: 如图所示,A是反比例函数图像上一点,过点A作ABy轴于点B,点P在x轴上,的面积为2,求反比例函数的解析式。 活动三: 拓展提升 双曲线y,y在第一象限的图像如图所示,点A在双曲线y=上,且AB//x轴,S=1,求y的函数关系式。 2、如图,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-和y=的图像交于A和B,若点C是x轴上任一点,连接AC,BC,求ABC的面积。 活动4:小结 同学们说说这节课你有哪些收获? 给学生足够的时间思考。 让学生谈谈自己的想法,其他同学补充。 师生共同完善该题,由学生归纳总结。 1、让学生有足够的时间思考。 老师作适当的引导,鼓励有想法的同学到讲台上去说出自己的解法。 师生共同完善该题的解题方法与步骤。 反思、归纳、总结。 若时间充足该题可以作为一道练习题。引导学生思考是否还存在AB//y轴的可能?三角形面积又如何求呢?同学们可以自己出出题,同学间交流讨论。 让尽量多的同学谈谈自己的收获 1、利用 几何画板学生能直观的观察到两三角形同底等高,面积相等。 2、培养学生养成善于反思、归纳、总结的习惯。 锻炼学生的表达能力和展现自我的勇气。例题的设置可以发散学生的思维。 分层教学,让基础好的同学有更多的收获,激发学生学习数学的兴趣,让他们体会成功的喜悦。 培养自己归纳总结的习惯
