华东师大版八年级下册数学 17.2.1 平面直角坐标系 课件 (共26张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 17.2.1 平面直角坐标系 课件 (共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
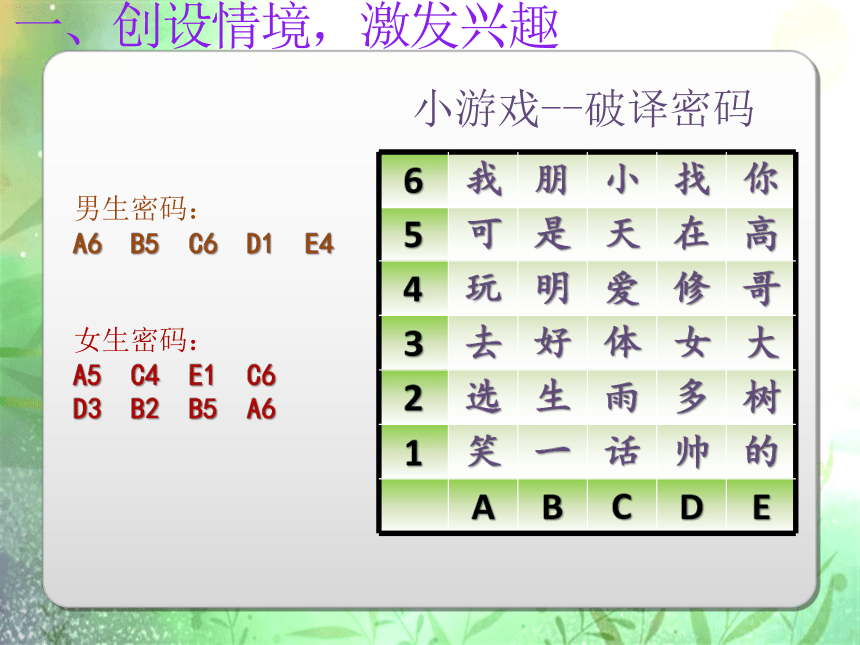
6 我 朋 小 找 你
5 可 是 天 在 高
4 玩 明 爱 修 哥
3 去 好 体 女 大
2 选 生 雨 多 树
1 笑 一 话 帅 的
A B C D E
小游戏--破译密码
男生密码:
A6 B5 C6 D1 E4
女生密码:
A5 C4 E1 C6
D3 B2 B5 A6
一、创设情境,激发兴趣
6 我 小
5 是
4 哥
3
2
1 帅
A B C D E
男生密码:
A6 B5 C6 D1 E4
破译密码--男生
教材分析
教法学法
教学评价
6 我 小
5 可 是
4 爱
3 女
2 生
1 的
A B C D E
女生密码:
A5 C4 E1 C6
D3 B2 B5 A6
破译密码—女生
讲台
1
2
3
4
5
6
1
2
3
4
5
6
7
8
若我们约定“排数在前,列数在后”。
冠军在我们中间!
你知道吗?
数学家笛卡儿 早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线。
1、理解平面直角坐标系的有关概念,掌握点与坐标的对应关系;
2、通过多个实例感受数形结合的思想;
3、激情投入,享受利用平面直角坐标系知识解决问题带来的乐趣。
学习目标
细读课本30—31页,认真思考下面3个问题,快速抢答:
1、在网格纸上画出平面直角坐标系,说一说它具有哪些特征?
2、平面上的点如何表示?
3、两条坐标轴如何把平面划分为四个象限?
二、亲身经历,初探新知
0
1
2
3
4
5
-4
-3
-2
-1
x
y
点A的横坐标为-4,
纵坐标为1,
有序数对(-4, 1)就叫做A的坐标
记作:A(-4,1)
A·
(-4,1)
点A(-4,1)到x轴距离为 ;到y轴的距离为 。
1
4
思考:点P(a,b)到x轴的距离为 ;
点P(a,b)到y轴的距离为 .
3
1
4
2
5
-2
-1
问题1、 在图17.2.2中分别描出点Q(2,3)、 S(-2,3)、R(3,-2) ; 问:Q(2,3)与P(3,2)是同一点吗? S(-2,3)与R(3,-2)是同一点吗?
这里得到的结果告诉我们什么?
三、研究实例,再探新知
问题1、 在图17.2.2中分别描出点Q(2,3)、 S(-2,3)、R(3,-2) ; 问:Q(2,3)与P(3,2)是同一点吗? S(-2,3)与R(3,-2)是同一点吗?
这里得到的结果告诉我们什么?
在平面直角坐标系中的点和有序实数对是一一对应的.
三、研究实例,再探新知
x
y
o
-1
2
3
4
-2
-3
-4
1
1
2
3
4
-1
-2
-3
B
C
A
F
E
D
(-1, -1)
问题2、写出图中A、B、C、D、E、F点的坐标,思考:
(1)在四个象限内的 点的坐标各有什么特征? (2)两条坐标轴上的点的坐标各有什么特征?
(+, +)
x
y
o
-1
2
3
4
-2
-3
-4
1
1
2
3
4
-1
-2
-3
B
C
A
F
E
D
(+, -)
(-, -)
(-, +)
(-1, -1)
问题2、写出图中A、B、C、D、E、F点的坐标,思考:
(1)在四个象限内的 点的坐标各有什么特征? (2)两条坐标轴上的点的坐标各有什么特征?
(+, +)
x
y
o
-1
2
3
4
-2
-3
-4
1
1
2
3
4
-1
-2
-3
(-1, 2)
B
C
A
F
E
D
(+, -)
(-, -)
(-, +)
(2, 1)
(2, -1)
(-1, -1)
(0, 3)
(-2, 0)
问题2、写出图中A、B、C、D、E、F点的坐标,思考:
(1)在四个象限内的 点的坐标各有什么特征? (2)两条坐标轴上的点的坐标各有什么特征?
坐标轴上的点的坐标中至少有一个是0;横轴上的点的纵坐标为0,纵轴上的点的横坐标为0.
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
问题3、在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
-4
-1
4
·
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
问题3、在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得到的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
中央电视台举办的《2014年中国数学坐标知识竞赛》总决赛今天举行。有五个城市代表队进入到了今天的总决赛,在5个代表队的背面,有5道不同难度的题目,若答对题目,可给本代表队获得相应的积分;若答错不得分。你会代表哪个城市进行最后的角逐呢?
四、快乐套餐,应用新知
若点M(a,b)在第四象限,则a,b的取值范围是( )
A、a<0 ,b<0 B、a>0 ,b>0
C、a>0 ,b<0 D、a<0 ,b<0
40分
C
当a>0,b<0时点M位于第几象限?
当ab>0时,点M位于第几象限?
当a为任意数时,且b<0时,点M在直角坐标系中的位置是什么?
点A(2,7)到x轴的距离为 ;
到y轴的距离为 .
10分
7
2
20分
右图是一个围棋棋盘,我们可以用类似于直角坐标系的方法表示各个棋子的位置.例如,图中最上方的一个棋子可以表示为(10,四).请至少说出图中四个棋子的“位置”.
o
2
3
4
5
1
x
y
-1
-2
1
3
4
2
-4
-2
-1
-3
-4
-3
A (2, -3)
A2 (-2, -3)
A3 (-2, 3)
A1 (2, 3)
50分
在网格纸上的直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴及原点的对称点,写出这些点的坐标,并总结规律。
归纳:关于x轴对称的两点,横坐标相等,纵坐标互为相反数;
关于y轴对称的两点,横坐标互为相反数,纵坐标相等;
o
2
3
4
5
1
x
y
-1
-2
1
3
4
2
-4
-2
-1
-3
-4
-3
A (2, -3)
A2 (-2, -3)
关于原点对称的两点,横坐标、纵坐标都互为相反数.
A3 (-2, 3)
A1 (2, 3)
50分
30分
恭喜你,请报一下你在在教室里的 坐标,并说出和你关于x轴、y轴对称的同学的名字,直接得分晋级.
谈谈通过本节课的学习,你有什么收获?和同伴交流一下。
五、归纳梳理,深化新知
1、平面直角坐标系的有关概念;
2、点与坐标的对应关系;
3、平面直角坐标系中坐标轴和各个象限上的点的坐标特征.
人生也有一个坐标系,时间是横轴,价值是纵轴,每一个人在这个坐标系中都有自己的定位。同学们:活出自己的精彩,实现自己的梦想,完成自己该做的事,你的人生将会越来越闪亮。加油!
请同学们课下收集身边运用坐标知识的例子,体会数学来源于生活又广泛应用于生活, 让我们一同学习有用的数学.
六、课后拓展,巩固新知
6 我 朋 小 找 你
5 可 是 天 在 高
4 玩 明 爱 修 哥
3 去 好 体 女 大
2 选 生 雨 多 树
1 笑 一 话 帅 的
A B C D E
小游戏--破译密码
男生密码:
A6 B5 C6 D1 E4
女生密码:
A5 C4 E1 C6
D3 B2 B5 A6
一、创设情境,激发兴趣
6 我 小
5 是
4 哥
3
2
1 帅
A B C D E
男生密码:
A6 B5 C6 D1 E4
破译密码--男生
教材分析
教法学法
教学评价
6 我 小
5 可 是
4 爱
3 女
2 生
1 的
A B C D E
女生密码:
A5 C4 E1 C6
D3 B2 B5 A6
破译密码—女生
讲台
1
2
3
4
5
6
1
2
3
4
5
6
7
8
若我们约定“排数在前,列数在后”。
冠军在我们中间!
你知道吗?
数学家笛卡儿 早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线。
1、理解平面直角坐标系的有关概念,掌握点与坐标的对应关系;
2、通过多个实例感受数形结合的思想;
3、激情投入,享受利用平面直角坐标系知识解决问题带来的乐趣。
学习目标
细读课本30—31页,认真思考下面3个问题,快速抢答:
1、在网格纸上画出平面直角坐标系,说一说它具有哪些特征?
2、平面上的点如何表示?
3、两条坐标轴如何把平面划分为四个象限?
二、亲身经历,初探新知
0
1
2
3
4
5
-4
-3
-2
-1
x
y
点A的横坐标为-4,
纵坐标为1,
有序数对(-4, 1)就叫做A的坐标
记作:A(-4,1)
A·
(-4,1)
点A(-4,1)到x轴距离为 ;到y轴的距离为 。
1
4
思考:点P(a,b)到x轴的距离为 ;
点P(a,b)到y轴的距离为 .
3
1
4
2
5
-2
-1
问题1、 在图17.2.2中分别描出点Q(2,3)、 S(-2,3)、R(3,-2) ; 问:Q(2,3)与P(3,2)是同一点吗? S(-2,3)与R(3,-2)是同一点吗?
这里得到的结果告诉我们什么?
三、研究实例,再探新知
问题1、 在图17.2.2中分别描出点Q(2,3)、 S(-2,3)、R(3,-2) ; 问:Q(2,3)与P(3,2)是同一点吗? S(-2,3)与R(3,-2)是同一点吗?
这里得到的结果告诉我们什么?
在平面直角坐标系中的点和有序实数对是一一对应的.
三、研究实例,再探新知
x
y
o
-1
2
3
4
-2
-3
-4
1
1
2
3
4
-1
-2
-3
B
C
A
F
E
D
(-1, -1)
问题2、写出图中A、B、C、D、E、F点的坐标,思考:
(1)在四个象限内的 点的坐标各有什么特征? (2)两条坐标轴上的点的坐标各有什么特征?
(+, +)
x
y
o
-1
2
3
4
-2
-3
-4
1
1
2
3
4
-1
-2
-3
B
C
A
F
E
D
(+, -)
(-, -)
(-, +)
(-1, -1)
问题2、写出图中A、B、C、D、E、F点的坐标,思考:
(1)在四个象限内的 点的坐标各有什么特征? (2)两条坐标轴上的点的坐标各有什么特征?
(+, +)
x
y
o
-1
2
3
4
-2
-3
-4
1
1
2
3
4
-1
-2
-3
(-1, 2)
B
C
A
F
E
D
(+, -)
(-, -)
(-, +)
(2, 1)
(2, -1)
(-1, -1)
(0, 3)
(-2, 0)
问题2、写出图中A、B、C、D、E、F点的坐标,思考:
(1)在四个象限内的 点的坐标各有什么特征? (2)两条坐标轴上的点的坐标各有什么特征?
坐标轴上的点的坐标中至少有一个是0;横轴上的点的纵坐标为0,纵轴上的点的横坐标为0.
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
问题3、在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
-4
-1
4
·
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
问题3、在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得到的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
中央电视台举办的《2014年中国数学坐标知识竞赛》总决赛今天举行。有五个城市代表队进入到了今天的总决赛,在5个代表队的背面,有5道不同难度的题目,若答对题目,可给本代表队获得相应的积分;若答错不得分。你会代表哪个城市进行最后的角逐呢?
四、快乐套餐,应用新知
若点M(a,b)在第四象限,则a,b的取值范围是( )
A、a<0 ,b<0 B、a>0 ,b>0
C、a>0 ,b<0 D、a<0 ,b<0
40分
C
当a>0,b<0时点M位于第几象限?
当ab>0时,点M位于第几象限?
当a为任意数时,且b<0时,点M在直角坐标系中的位置是什么?
点A(2,7)到x轴的距离为 ;
到y轴的距离为 .
10分
7
2
20分
右图是一个围棋棋盘,我们可以用类似于直角坐标系的方法表示各个棋子的位置.例如,图中最上方的一个棋子可以表示为(10,四).请至少说出图中四个棋子的“位置”.
o
2
3
4
5
1
x
y
-1
-2
1
3
4
2
-4
-2
-1
-3
-4
-3
A (2, -3)
A2 (-2, -3)
A3 (-2, 3)
A1 (2, 3)
50分
在网格纸上的直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴及原点的对称点,写出这些点的坐标,并总结规律。
归纳:关于x轴对称的两点,横坐标相等,纵坐标互为相反数;
关于y轴对称的两点,横坐标互为相反数,纵坐标相等;
o
2
3
4
5
1
x
y
-1
-2
1
3
4
2
-4
-2
-1
-3
-4
-3
A (2, -3)
A2 (-2, -3)
关于原点对称的两点,横坐标、纵坐标都互为相反数.
A3 (-2, 3)
A1 (2, 3)
50分
30分
恭喜你,请报一下你在在教室里的 坐标,并说出和你关于x轴、y轴对称的同学的名字,直接得分晋级.
谈谈通过本节课的学习,你有什么收获?和同伴交流一下。
五、归纳梳理,深化新知
1、平面直角坐标系的有关概念;
2、点与坐标的对应关系;
3、平面直角坐标系中坐标轴和各个象限上的点的坐标特征.
人生也有一个坐标系,时间是横轴,价值是纵轴,每一个人在这个坐标系中都有自己的定位。同学们:活出自己的精彩,实现自己的梦想,完成自己该做的事,你的人生将会越来越闪亮。加油!
请同学们课下收集身边运用坐标知识的例子,体会数学来源于生活又广泛应用于生活, 让我们一同学习有用的数学.
六、课后拓展,巩固新知
