高二下数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析单元检测卷(word版含解析)
文档属性
| 名称 | 高二下数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析单元检测卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 708.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览



文档简介
第八章成对数据的统计分析单元检测卷
一、单选题
1.在研究某高中高三年级学生的性别与是否喜欢某学科的关系时,总共调查了N个学生(),其中男女学生各半,男生中60%表示喜欢该学科,其余表示不喜欢;女生中40%表示喜欢该学科,其余表示不喜欢.若有99.9%把握认为性别与是否喜欢该学科有关,则可以推测N的最小值为( )
附,
0.050 0.010 0.001
3.841 6.635 10.828
A.400 B.300 C.200 D.100
2.某中学共有1000人,其中男生700人,女生300人,为了了解该校学生每周平均体育锻炼时间的情况以及经常进行体育锻炼的学生是否与性别有关(经常进行体育锻炼是指:周平均体育锻炼时间不少于4小时),现在用分层抽样的方法从中收集200位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如图.已知在样本数据中,有40位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理( )
附:,其中.
0.10 0.05 0.01 0.005
2.706 3.841 6.635 7.879
A.有95%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
B.有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C.有90%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D.有95%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
3.已知变量x,y之间具有较强的线性相关性,测得它们的四组数据如表所示:
x 1 2 3 4
y
现已求得变量x,y之间的回归方程为,请根据给出的条件,预测时,y的值约为( )A. B. C. D.
4.已知,.
0.050 0.010
3.841 6.635
在“数学文化大讲堂”活动中,某老师对“学生性别和喜欢数学文化是否有关”作了一次调查,其中被调查的女生人数是男生人数的,男生喜欢数学文化的人数占男生人数的,女生喜欢数学文化的人数占女生人数,若有的把握认为是否喜欢数学文化和性别有关,则男生至少有( )A.24人 B.22人 C.20人 D.18人
5.已知变量与,且观测数据如下表(其中,),则由该观测的数据算得的线性回归方程可能是( )
1 2 3 4 5
6.5 4 1
A. B.
C. D.
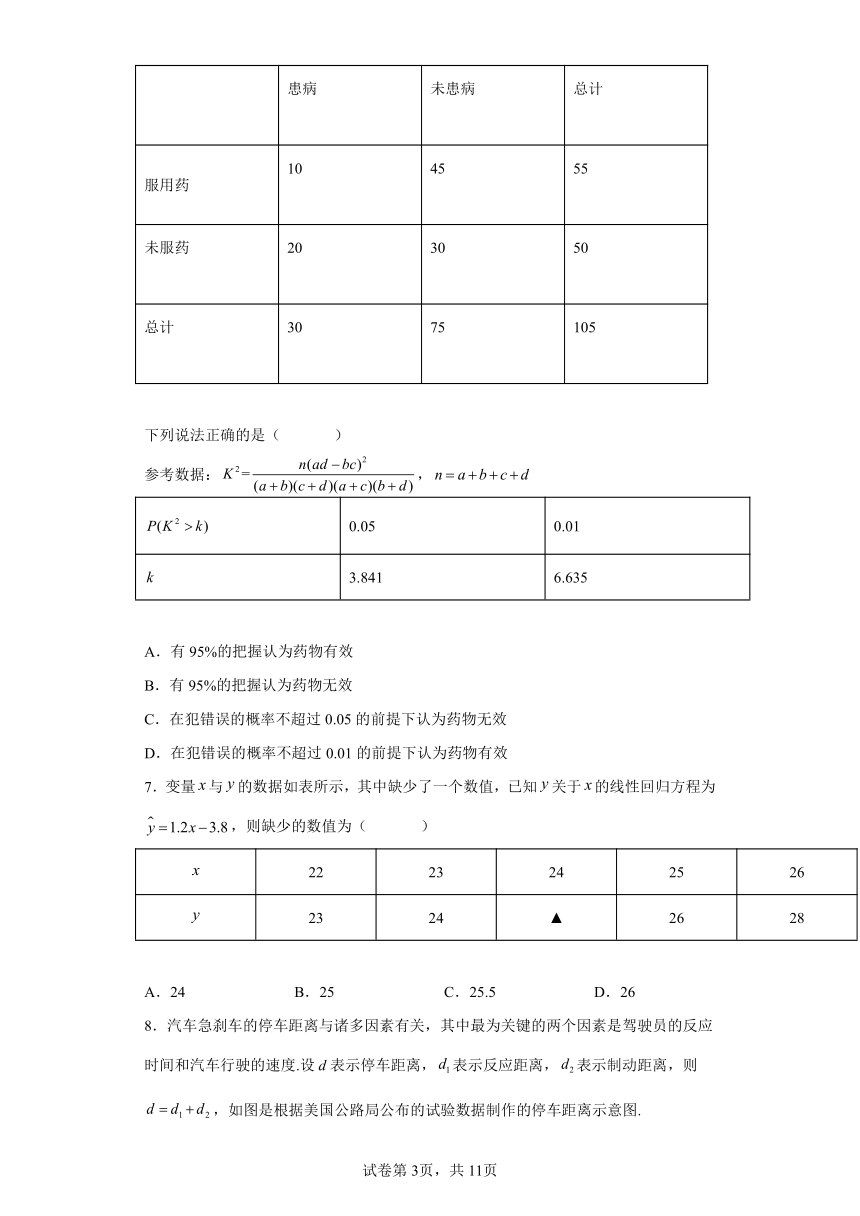
6.新型冠状病毒(2019-NCoV)因2019年武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名,为考察某种药物预防该疾病的效果,进行动物试验,得到如下列联表:
患病 未患病 总计
服用药 10 45 55
未服药 20 30 50
总计 30 75 105
下列说法正确的是( )
参考数据:,
0.05 0.01
3.841 6.635
A.有95%的把握认为药物有效
B.有95%的把握认为药物无效
C.在犯错误的概率不超过0.05的前提下认为药物无效
D.在犯错误的概率不超过0.01的前提下认为药物有效
7.变量与的数据如表所示,其中缺少了一个数值,已知关于的线性回归方程为,则缺少的数值为( )
22 23 24 25 26
23 24 ▲ 26 28
A.24 B.25 C.25.5 D.26
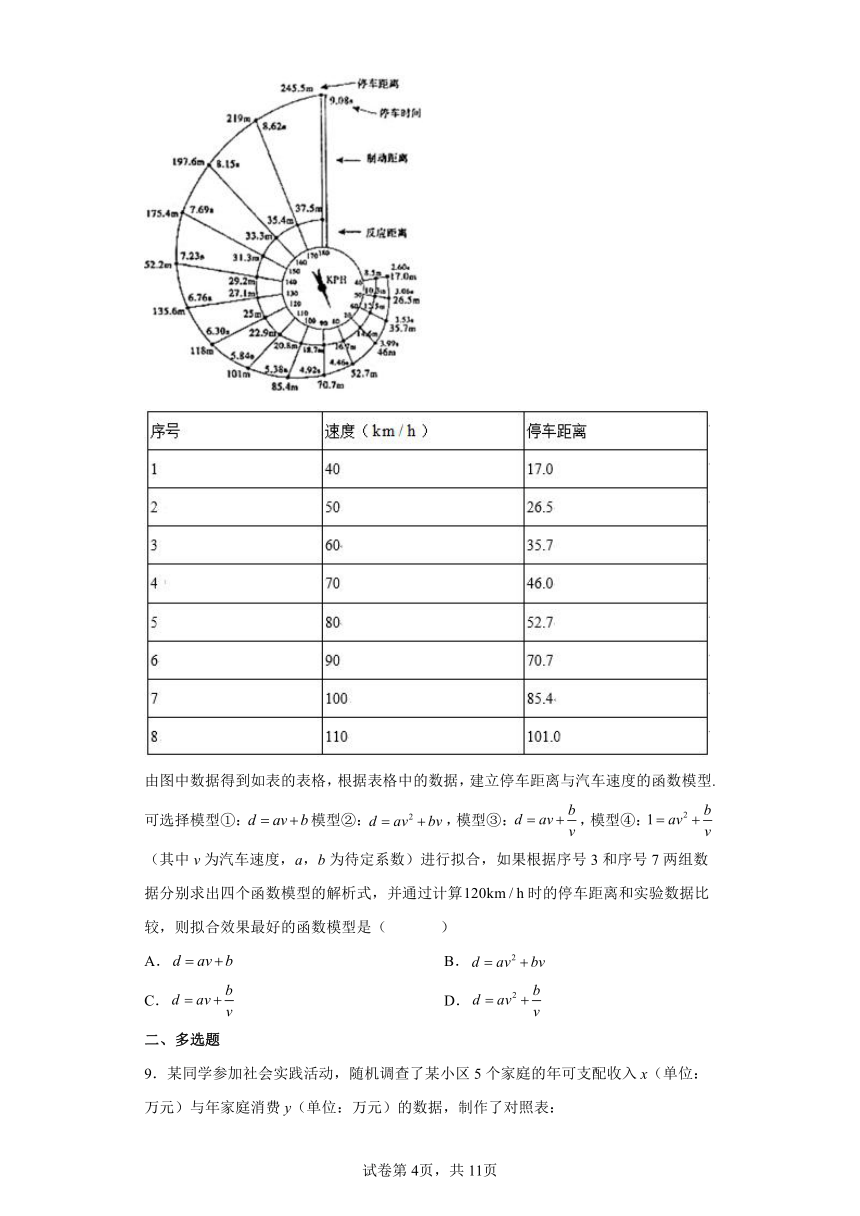
8.汽车急刹车的停车距离与诸多因素有关,其中最为关键的两个因素是驾驶员的反应时间和汽车行驶的速度.设d表示停车距离,表示反应距离,表示制动距离,则,如图是根据美国公路局公布的试验数据制作的停车距离示意图.
由图中数据得到如表的表格,根据表格中的数据,建立停车距离与汽车速度的函数模型.可选择模型①:模型②:,模型③:,模型④:(其中v为汽车速度,a,b为待定系数)进行拟合,如果根据序号3和序号7两组数据分别求出四个函数模型的解析式,并通过计算时的停车距离和实验数据比较,则拟合效果最好的函数模型是( )
A. B.
C. D.
二、多选题
9.某同学参加社会实践活动,随机调查了某小区5个家庭的年可支配收入x(单位:万元)与年家庭消费y(单位:万元)的数据,制作了对照表:
x/万元 2.7 2.8 3.1 3.5 3.9
y/万元 1.4 1.5 1.6 1.8 2.2
由表中数据得回归直线方程为,得到下列结论,其中正确的是( )A.若某户年可支配收入为4万元时,则年家庭消费约为2.3万元
B.若某户年可支配收入为4万元时,则年家庭消费约为2.1万元
C.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.5万元
D.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.1万元
10.下列说法中正确的是( )
A.将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变
B.设有一个回归方程,变量x增加一个单位时,y平均增加5个单位
C.回归方程必过散点中的某个点
D.在一个列联表中,由计算得,则有99%的把握确认这两个变量间有关系参考公式:附:
0.025 0.010 0.005 0.001
k 5.024 6.635 7.879 10.828
11.某企业节能降耗技术改造后,在生产某产品过程中记录的产量(吨)与相应的生产能耗(吨)的几组对应数据如表,现发现表中有个数据看不清,已知回归直线方程为,下列说法正确的是( )
2 3 4 5 6
19 25 38 44
A.看不清的数据的值为34
B.具有正相关关系,相关系数
C.第三个样本点对应的残差
D.据此模型预测产量为7吨时,相应的生产能耗约为50吨
12.对具有线性相关关系的变量,有一组观测数据,,下列说法中正确的是( )
A.数据的平均数为1
B.将数据中的每个数都加上同一个常数,所得新数据方差恒不变
C.若数据的线性回归方程是,则实数
D.变量,的线性相关系数越大,两个变量,的线性相关性越强
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.2018年春季,世界各地相继出现流感疫情,这已经成为全球性的公共卫生问题.为了考查某种流感疫苗的效果,某实验室随机抽取100只健康小鼠进行试验,得到如下列联表:
感染 未感染 总计
注射 10 40 50
未注射 20 30 50
总计 30 70 100
参照附表,在犯错误的概率最多不超过____的前提下,可认为“注射疫苗”与“感染流感”有关系.
【参考公式:.】
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
14.已知一组数据确定的回归直线方程为,且,发现两组数据,误差较大,去掉这两组数据后,重新求得回归直线的斜率为,当时,____________.
15.已知下列命题:
①在线性回归模型中,相关指数表示解释变量对于预报变量的贡献率,越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数的绝对值就越接近于1;
③在回归直线方程中,当解释变量每增加一个单位时,预报变量平均减少0.5个单位;
④对分类变量与,它们的随机变量的观测值来说,越小,“与有关系”的把握程度越大.其中正确命题的序号是__________.
16.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价(元) 4 5 6 7 8 9
销量(件) 90 84 83 80 75 68
由表中数据,求得线性回归方程为,则实数______.
四、解答题
17.某机构为了解市民对交通的满意度,随机抽取了100位市民进行调查结果如下:回答“满意”的人数占总人数的一半,在回答“满意”的人中,“上班族”的人数是“非上班族”人数的;在回答“不满意”的人中,“非上班族”占.
(1)请根据以上数据填写下面列联表,并依据小概率值的独立性检验,分析能否认为市民对于交通的满意度与是否为上班族存关联?
满意 不满意 合计
上班族
非上班族
合计
(2)为了改善市民对交通状况的满意度,机构欲随机抽取部分市民做进一步调查.规定:抽样的次数不超过,若随机抽取的市民属于不满意群体,则抽样结束;若随机抽取的市民属于满意群体,则继续抽样,直到抽到不满意市民或抽样次数达到时,抽样结束.
(i)若,写出的分布列和数学期望;
(ii)请写出的数学期望的表达式(不需证明),根据你的理解说明的数学期望的实际意义.
附:
参考公式:,其中.
18.第24届冬季奥林匹克运动会将于2022年2月4日至20日在北京举行,践行“绿色奥运 科技奥运 人文奥运”理念,举办一届“有特色 高水平”的奥运会,是中国向世界的庄严承诺.为宣传北京冬奥会,某市开展了冬奥知识竞答活动.从参与的市民中随机抽取100人,统计他们的竞答成绩得到下面的列联表(单位:人).
成绩合格 成绩不合格 合计
男性 40 50
女性 20
合计
(1)完成列联表,并估计该市参与此次冬奥知识竞答的市民的成绩合格率;
(2)根据列联表判断是否有95%的把握认为该市参与此次冬奥知识竞答的市民的成绩与性别有关?
参考公式:
19.手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式.在某市随机调查了200名顾客购物时使用手机支付的情况,得到如下的2×2列联表.已知从使用手机支付的人群中随机抽取1人,抽到青年的概率为.
(1)根据已知条件完成2×2列联表,并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”?
2×2列联表:
青年 中老年 总计
使用手机支付 120
不使用手机支付 48
总计 200
(2)现采用分层抽样的方法从这200名顾客中按照“使用手机支付”和“不使用手机支付”抽取得到一个容量为5的样本,设事件A为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件A发生的概率.
附:,其中n=a+b+c+d,
P(K2≥k0) 0.05 0.025 0.010 0.005
k0 3.841 5.024 6.635 7.879
20.疫苗是指用各种病原微生物制作的用于预防接种的生物制品,接种疫苗是预防和控制传染病最经济 有效的公共卫生干预措施.某制药厂对预防某种疾病的两种疫苗开展临床对比试验.若使用后的抗体呈阳性,则认为疫苗有效.在已经接种疫苗的群体中随机抽取的100个样本,其中有60个接种了灭活疫苗,剩余40个接种了核酸疫苗.根据样本数据绘制等高条形图(如图所示),其中两个深色条的高分别表示接种灭活疫苗和核酸疫苗样本中抗体呈阳性的频率.现从这100个样本中随机抽取1人,已知事件“该样本接种了灭活疫苗且抗体呈阳性”发生的概率为0.54.
(1)求等高条形图中a的值;
(2)请在答题卷中完成下面的列联表,并判断能否在犯错概率不超过0.10的前提下认为两种疫苗的预防效果存在差异?
灭活疫苗 核酸疫苗 总计
抗体为阳性
抗体为阴性
总计 60 40 100
参考公式:,其中
0.15 0.10 0.01
2.072 2.706 6.635
21.“双减”政策明确指出要通过阅读等活动,充分用好课后服务时间,为学有余力的学生拓展学习空间.某家庭有小明和小红两个孩子,父母每天为他们安排了自由阅读的时间,约定周一到周日每天的阅读时间不能比前一天少.为了调查两人自由阅读时间的情况,父亲记录了两人某周每天的阅读时间(单位:min),如下表所示,其中小明周日的阅读时间a忘了记录,但知道,.
周一 周二 周三 周四 周五 周六 周日
序号x 1 2 3 4 5 6 7
小明的阅读时间y/min 16 20 20 25 30 36 a
小红的阅读时间z/min 16 22 25 26 32 35 35
(1)求小明这一周的阅读时间超过小红这一周的阅读时间的概率;
(2)根据小明这一周前6天的阅读时间,求其阅读时间y关于序号x的线性回归方程,并估计小明周日阅读时间a的值.
参考公式:回归方程中斜率与截距的最小二乘估计公式分别为,.
22.2021年春节前,受疫情影响,各地鼓励外来务工人员选择就地过年.某市统计了该市4个地区的外来务工人数与就地过年人数(单位:万),得到如下表格:
A区 B区 C区 D区
外来务工人数x/万 3 4 5 6
就地过年人数y/万 2.5 3 4 4.5
(1)请用相关系数说明y与x之间的关系可用线性回归模型拟合,并求关于的线性回归方程.
(2)假设该市政府对外来务工人员中选择就地过年的每人发放1000元补贴.
(i)若该市E区有2万名外来务工人员,根据(1)的结论估计该市政府需要给E区就地过年的人员发放的补贴总金额;
(ii)若A区的外来务工人员中甲 乙选择就地过年的概率分别为,,该市政府对甲 乙两人的补贴总金额的期望不超过1500元,求的取值范围.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据题目列出列联表,再根据列联表的数据计算值,进而得到关于的关系式,求解即可.
【详解】
由题可知,男女各人,列联表如下:
喜欢 不喜欢 总计
男 30m 20m 50m
女 20m 30m 50m
总计 50m 50m 100m
,
有99.9%把握认为性别与是否喜欢该学科有关,
,解得,
,
,
.
故选:B
2.B
【解析】
根据分层抽样以及频率分布直方图列联表,再计算,结合表中的数据判断即可.
【详解】
由频率分布直方图可知, 平均体育锻炼时间不少于4小时的频率为,故经常进行体育锻炼的学生人.又其中有40位女生的每周平均体育锻炼时间超过4小时,故有位男生经常锻炼.根据分层抽样的方法可知,样本中男生的人数为,女生有.列出列联表有:
男生 女生 总计
经常锻炼 110 40 150
不经常锻炼 30 20 50
总计 140 60 200
故,因为.
故有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”.
故选:B
【点睛】
本题主要考查了分层抽样以及频率分布直方图的运用,同时也考查了独立性检验在实际情景中的运用.属于中档题.
3.B
【解析】
【分析】
由已知求得,,代入求得a值,则线性回归方程可求,取求得y值即可.
【详解】
,,
,则线性回归方程为,
取,得.
故选:B.
【点睛】
本题考查线性回归方程,明确线性回归方程恒过样本点的中心是关键,是基础题.
4.D
【解析】
【分析】
设男生至少有人,根据条件,列出联表,计算出,令6.635,即可求出.
【详解】
设男生至少有人,根据题意,可列出如下联表:
喜欢数学文化 不喜欢数学文化 总计
男生
女生
总计
则,
若有的把握认为是否喜欢数学文化和性别有关,
则,即,
解得,
由于表中人数都为整数,所以,
即男生至少有18人.
故选:D.
【点睛】
本题考查独立性检验,属于基础题.
5.C
【解析】
【分析】
求出,代入方程检验,然后根据的变化趋势判系数的正负可得.
【详解】
由题意,,
把代入各方程,A中,,同理有B中,,C中,D中,,
又表格中数据随着的增大,减小,因此它们负相关,的系数为负.
故选:C.
【点睛】
在求线性回归方程时,可观察已知数据,呈线性相关的数据,如果随的增大,也增大,则与是正相关,在回归直线方程中的系数为正,反之为负.
6.A
【解析】
【分析】
根据列联表计算,对照临界值即可得出结论.
【详解】
根据列联表,计算,
由临界值表可知,
有95%的把握认为药物有效,A正确
故选:A
7.A
【解析】
【分析】
可设出缺少的数值,利用表中的数据,分别表示出、,将样本中心点带入回归方程,即可求得参数.
【详解】
设缺少的数值为,则,,
因为回归直线方程经过样本点的中心,所以,解得.
故选:A.
8.B
【解析】
【分析】
分别根据表中数据基础出四种函数模型的解析式,然后代入各解析式,计算出各模型在时的停车距离的估计值,然后和实验数据118进行比较,最接近的拟合效果最好.
【详解】
若选择模型①,则,解得,,
故,
当时,停车距离d的预测值为,
若选择模型②,则,解得,,
故,
当时,停车距离d的预测值为,
若选择模型③,则,解得,,
故,
当时,停车距离d的预测值为,
若选择模型④,则,解得,,
故,
当时,停车距离d的预测值为,
由实验数据可知当时,停车距离为,
故模型②的预测值更接近,故模型②拟合效果最好.
故选:B.
【点睛】
本题考查利用函数模型拟合变量间的相关关系,考查学生的计算能力,属于中档题.
9.BC
【解析】
【分析】
先求出样本中心点的坐标,再求出,即可判断得解.
【详解】
由题得,
,
所以.
所以.
当时,,所以选项B正确,选项A错误;
因为,
所以若年可支配收入每增加1万元,则年家庭消费相应平均增加0.5万元,
所以选项C正确,选项D错误.
故选:BC
【点睛】
本题主要考查线性回归方程的求法和应用,意在考查学生对这些知识的理解掌握水平,属于基础题.
10.AD
【解析】
【分析】
根据方差的计算公式,回归直线与回归方程的含义,独立性检验的概念判断各选项.
【详解】
解:A,将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;由于平均值增加相同的值,故A正确;
B,在回归直线方程中,当解释变量x每增加一个单位时,故预报变平均减少5个单位,故B不正确;
C,回归方程,可能不过散点中的任何一个点,故C不正确;
D.在列联表中,由计算得,对照临界值得,有99%的把握确认这两个变量间有关系,故D正确
故选:AD.
11.ACD
【解析】
【分析】
利用回归直线方程结合各选项的条件逐一分析计算即可判断作答.
【详解】
对于A,,由回归直线方程得,则,A正确;
对于B,由回归直线方程及数表知,具有正相关关系,而相关系数的绝对值不超过1,B不正确;
对于C,第三个样本点对应的残差,C正确;
对于D,在回归直线方程中,时,生产能耗约(吨) ,D正确.
故选:ACD
12.ABC
【解析】
【分析】
由题知,再结合题意依次讨论各选项即可得答案.
【详解】
解:因为,,
所以,,
所以对于A选项,的平均数为,故正确;
对于B选项,数据中的每个数都加上同一个常数,方差不变,故正确;
对与C选项,若数据的线性回归方程是,则,故正确;
对于D选项,当变量,的线性负相关时,相关系数越大,两个变量,的线性相关性越弱,故错误;
故选:ABC
13.0.05
【解析】
【详解】
分析:直接利用独立性检验公式计算即得解.
详解:由题得,
所以犯错误的概率最多不超过0.05的前提下,可认为“注射疫苗”与“感染流感”有关系.
故答案为0.05.
点睛:本题主要考查独立性检验和的计算,意在考查学生对这些知识的掌握水平和解决实际问题的能力.
14.5
【解析】
【详解】
分析:由题意求出样本中心点,然后求出新数据的样本中心,利用回归直线的斜率估计值为,求出新的回归方程,然后再计算时的值.
详解:∵一组数据确定的回归直线方程为,且,
∴,
解得,
∴原数据的样本中心点为(2,4).
由题意得去掉数据后新数据的样本中心为(2,4),重新求得的回归直线的斜率估计值为,
∴可设新的回归直线方程设为,
将点(2,4)代入上式后得,
解得,
∴新的回归直线的方程为,
将代入回归直线方程求得.
点睛:线性回归方程过样本中心点是重要的结论,利用此结论可求回归直线中的参数,也可求原样本数据中的参数.另外,根据线性回归方程可进行估计和预测.
15.①②③
【解析】
【详解】
①相关指数表示解释变量对于预报变量的贡献率,越接近于1,表示回归效果越好;是正确的;②两个变量相关性越强,则相关系数r的绝对值就越接近于1,是正确的;③在回归直线方程中,当解释变量每增加一个单位时,预报变量平均减少0.5个单位是正确的,因为回归方程,并不是样本点都落在方程上,故只能是估计值,所以说是平均增长;④对分类变量与,它们的随机变量的观测值来说,越小,“与有关系”的把握程度越小;故原命题错误;
故答案为①②③.
16.106
【解析】
【分析】
求出样本中心坐标,代入回归方程即可求出值.
【详解】
解:,,
将代入回归方程得,
解得.
故答案为:.
【点睛】
本题考查回归方程问题,属于基础题.
17.(1)列联表见解析,市民对交通的满意度与是否上班有关,此推断犯错误的概率不大于0.001
(2)(i)分布列见解析,;(ii),平均每抽取2个人,就会有一个不满意的市民
【解析】
【分析】
(1)根据题意完成列联表,进而利用公式计算可得,查表分析可得结果;
(2)(i)由(1)可知市民的满意度和不满意度均为,计算可得的分布列和数学期望,(ⅱ)由(i)可得,当n趋向于正无穷大时,趋向于2,即可理解为平均每抽取2个人,就会有一个不满意的市民.
(1)
由题意可知
满意 不满意 合计
上班族 15 40 55
非上班族 35 10 45
合计 50 50 100
零假设为:市民对交通的满意度与是否上班独立,
因为;
根据小概率值的独立性检验,我们推断不成立,即认为市民对交通的满意度与是否上班有关,此推断犯错误的概率不大于0.001.
(2)
(i)当时,的取值为1,2,3,4,5,
由(1)可知市民的满意度和不满意度均为;
所以,,,,,
所以的分布列为
1 2 3 4 5
P
所以;
(ⅱ)
当n趋向于正无穷大时,趋向于2,此时恰好为不满意度的倒数;
也可以理解为平均每抽取2个人,就会有一个不满意的市民.
18.(1)列联表答案见解析,估计该市参与此次冬奥知识竞答的市民的成绩合格率为0.7
(2)有95%的把握认为该市参与此次冬奥知识竞答的市民的成绩与性别有关
【解析】
【分析】
(1)根据题意完成列联表,进而可得该市参与此次冬奥知识竞答的市民的成绩合格率;
(2)利用卡方的计算公式求出观测值,与3.841比大小即可得出结果.
(1)
完成列联表(单位:人)
成绩合格 成绩不合格 合计
男性 40 10 50
女性 30 20 50
合计 70 30 100
由列联表,从参与的市民中随机抽取100人,有70人竞答成绩合格,
所以估计该市参与此次冬奥知识竞答的市民的成绩合格率为0.7.
(2)
由列联表,的观测值,
∴有95%的把握认为该市参与此次冬奥知识竞答的市民的成绩与性别有关.
19.(1)表格见解析,有
(2)
【解析】
【分析】
(1)根据抽到青年的概率为,得到使用手机支付的人群中的青年的人数和中老年的人数,完成2×2列联表,再求得K2的观测值,再与临界值表对照下结论;
(2)由分层抽样,得到使用手机支付的人数和不使用手机支付的人数,利用古典概型的概率求解.
(1)
解:∵从使用手机支付的人群中随机抽取1人,抽到青年的概率为,
∴使用手机支付的人群中的青年的人数为×120=84.
则使用手机支付的人群中的中老年的人数为120-84=36,
所以2×2列联表为:
青年 中老年 总计
使用手机支付 84 36 120
不使用手机支付 32 48 80
总计 116 84 200
K2的观测值k==≈17.734.
∵17.734>7.879,P(K2≥7.879)=0.005,
故有99.5%的把握认为“市场购物用手机支付与年龄有关”.
(2)
这200名顾客中采用分层抽样,从“使用手机支付”和“不使用手机支付”中抽到一个容量为5的样本中:
使用手机支付的人有5×=3人,记编号为1,2,3.
不使用手机支付的人有2人,记编号为a,b.
则从这个样本中任选2人有(1,2),(1,3),(1,a),(1,b),(2,3),(2,a),(2,b),(3,a),(3,b),(a,b)共10种.
其中至少有1人是不使用手机支付的有(1,a),(1,b),(2,a),(2,b),(3,a),(3,b),(a,b)共7种.
故所求事件A的概率P(A)=.
20.(1)
(2)列联表答案见解析,不能在犯错概率不超过0.10的前提下认为两种疫苗的预防效果存在差异
【解析】
【分析】
(1)根据题意得,解方程即可得答案;
(2)结合题意得接种灭活疫苗抗体阳性的共有人,接种核酸疫苗后抗体呈阳性的共有人,进而完成列联表,结合独立性检验求解即可.
(1)
解:依题意“1名受访者接种灭活疫苗且接种后抗体呈阳性”发生的概率为0.54,
所以
解得,所以
(2)
解:根据题意,接种灭活疫苗抗体阳性的共有:人,
接种核酸疫苗后抗体呈阳性的共有:人,
故列联表如下:
灭活疫苗 核酸疫苗 总计
抗体为阳性 54 34 88
抗体为阴性 6 6 12
总计 60 40 100
零假设为接种两种疫苗效果无差异
根据列联表中的数据,得到
因为
所以不能在犯错概率不超过0.10的前提下认为两种疫苗的预防效果存在差异.
21.(1);
(2),38.
【解析】
【分析】
(1)由,可得a的所有可能取值,计算出超过小红的阅读时间的a的可能取值即可计算作答.
(2)根据给定数表算出最小二乘估计公式中的相关量,再代入公式计算即可,并估计a的值.
(1)
依题意,,,则a的取值一共有25个不同结果,它们等可能,
令,解得,
因此,当小明这一周的阅读时间超过小红这一周的阅读时间时,a的取值一共有16个不同结果,
所以小明这一周的阅读时间超过小红这一周的阅读时间的概率为.
(2)
由数表得:,,
,,
所以,则,
所以y关于x的线性回归方程为,
当时,,
所以估计小明周日阅读时间a的值为38.
22.(1)说明答案见解析,
(2)(i)(万元);(ii)
【解析】
【分析】
(1)根据相关系数的绝对值越接近1,线性回归模型的拟合效果越好,即可以根据直接计算相关系数的值来判断与之间的线性相关程度的强弱;关于的线性回归方程直接用参考公式求解.
(2)(i)将代入(1)中的线性回归方程,即可求出E区就地过年的人数;
(ii)由X的所有可能取值为0,1,2,并分别求出相应的概率,即可得到分布列,然后求出期望,最后列出不等式求出的取值范围.
(1)
(1)由题,,,
,
,
,
所以相关系数,
因为y与x之间的相关系数近似为0.99,说明y与x之间的线性相关程度非常强,所以可用线性回归模型拟合y与x之间的关系.
,,
故y关于x的线性回归方程为.
(2)
(2)(i)将代入,得,
故估计该市政府需要给E区就地过年的人员发放的补贴总金额为(万元).
(ii)设甲 乙两人中选择就地过年的人数为X,则X的所有可能取值为0,1,2,
,
,
.
所以,
所以,
由,得,
又,所以,
故的取值范围为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在研究某高中高三年级学生的性别与是否喜欢某学科的关系时,总共调查了N个学生(),其中男女学生各半,男生中60%表示喜欢该学科,其余表示不喜欢;女生中40%表示喜欢该学科,其余表示不喜欢.若有99.9%把握认为性别与是否喜欢该学科有关,则可以推测N的最小值为( )
附,
0.050 0.010 0.001
3.841 6.635 10.828
A.400 B.300 C.200 D.100
2.某中学共有1000人,其中男生700人,女生300人,为了了解该校学生每周平均体育锻炼时间的情况以及经常进行体育锻炼的学生是否与性别有关(经常进行体育锻炼是指:周平均体育锻炼时间不少于4小时),现在用分层抽样的方法从中收集200位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如图.已知在样本数据中,有40位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理( )
附:,其中.
0.10 0.05 0.01 0.005
2.706 3.841 6.635 7.879
A.有95%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
B.有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C.有90%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D.有95%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
3.已知变量x,y之间具有较强的线性相关性,测得它们的四组数据如表所示:
x 1 2 3 4
y
现已求得变量x,y之间的回归方程为,请根据给出的条件,预测时,y的值约为( )A. B. C. D.
4.已知,.
0.050 0.010
3.841 6.635
在“数学文化大讲堂”活动中,某老师对“学生性别和喜欢数学文化是否有关”作了一次调查,其中被调查的女生人数是男生人数的,男生喜欢数学文化的人数占男生人数的,女生喜欢数学文化的人数占女生人数,若有的把握认为是否喜欢数学文化和性别有关,则男生至少有( )A.24人 B.22人 C.20人 D.18人
5.已知变量与,且观测数据如下表(其中,),则由该观测的数据算得的线性回归方程可能是( )
1 2 3 4 5
6.5 4 1
A. B.
C. D.
6.新型冠状病毒(2019-NCoV)因2019年武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名,为考察某种药物预防该疾病的效果,进行动物试验,得到如下列联表:
患病 未患病 总计
服用药 10 45 55
未服药 20 30 50
总计 30 75 105
下列说法正确的是( )
参考数据:,
0.05 0.01
3.841 6.635
A.有95%的把握认为药物有效
B.有95%的把握认为药物无效
C.在犯错误的概率不超过0.05的前提下认为药物无效
D.在犯错误的概率不超过0.01的前提下认为药物有效
7.变量与的数据如表所示,其中缺少了一个数值,已知关于的线性回归方程为,则缺少的数值为( )
22 23 24 25 26
23 24 ▲ 26 28
A.24 B.25 C.25.5 D.26
8.汽车急刹车的停车距离与诸多因素有关,其中最为关键的两个因素是驾驶员的反应时间和汽车行驶的速度.设d表示停车距离,表示反应距离,表示制动距离,则,如图是根据美国公路局公布的试验数据制作的停车距离示意图.
由图中数据得到如表的表格,根据表格中的数据,建立停车距离与汽车速度的函数模型.可选择模型①:模型②:,模型③:,模型④:(其中v为汽车速度,a,b为待定系数)进行拟合,如果根据序号3和序号7两组数据分别求出四个函数模型的解析式,并通过计算时的停车距离和实验数据比较,则拟合效果最好的函数模型是( )
A. B.
C. D.
二、多选题
9.某同学参加社会实践活动,随机调查了某小区5个家庭的年可支配收入x(单位:万元)与年家庭消费y(单位:万元)的数据,制作了对照表:
x/万元 2.7 2.8 3.1 3.5 3.9
y/万元 1.4 1.5 1.6 1.8 2.2
由表中数据得回归直线方程为,得到下列结论,其中正确的是( )A.若某户年可支配收入为4万元时,则年家庭消费约为2.3万元
B.若某户年可支配收入为4万元时,则年家庭消费约为2.1万元
C.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.5万元
D.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.1万元
10.下列说法中正确的是( )
A.将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变
B.设有一个回归方程,变量x增加一个单位时,y平均增加5个单位
C.回归方程必过散点中的某个点
D.在一个列联表中,由计算得,则有99%的把握确认这两个变量间有关系参考公式:附:
0.025 0.010 0.005 0.001
k 5.024 6.635 7.879 10.828
11.某企业节能降耗技术改造后,在生产某产品过程中记录的产量(吨)与相应的生产能耗(吨)的几组对应数据如表,现发现表中有个数据看不清,已知回归直线方程为,下列说法正确的是( )
2 3 4 5 6
19 25 38 44
A.看不清的数据的值为34
B.具有正相关关系,相关系数
C.第三个样本点对应的残差
D.据此模型预测产量为7吨时,相应的生产能耗约为50吨
12.对具有线性相关关系的变量,有一组观测数据,,下列说法中正确的是( )
A.数据的平均数为1
B.将数据中的每个数都加上同一个常数,所得新数据方差恒不变
C.若数据的线性回归方程是,则实数
D.变量,的线性相关系数越大,两个变量,的线性相关性越强
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.2018年春季,世界各地相继出现流感疫情,这已经成为全球性的公共卫生问题.为了考查某种流感疫苗的效果,某实验室随机抽取100只健康小鼠进行试验,得到如下列联表:
感染 未感染 总计
注射 10 40 50
未注射 20 30 50
总计 30 70 100
参照附表,在犯错误的概率最多不超过____的前提下,可认为“注射疫苗”与“感染流感”有关系.
【参考公式:.】
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
14.已知一组数据确定的回归直线方程为,且,发现两组数据,误差较大,去掉这两组数据后,重新求得回归直线的斜率为,当时,____________.
15.已知下列命题:
①在线性回归模型中,相关指数表示解释变量对于预报变量的贡献率,越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数的绝对值就越接近于1;
③在回归直线方程中,当解释变量每增加一个单位时,预报变量平均减少0.5个单位;
④对分类变量与,它们的随机变量的观测值来说,越小,“与有关系”的把握程度越大.其中正确命题的序号是__________.
16.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价(元) 4 5 6 7 8 9
销量(件) 90 84 83 80 75 68
由表中数据,求得线性回归方程为,则实数______.
四、解答题
17.某机构为了解市民对交通的满意度,随机抽取了100位市民进行调查结果如下:回答“满意”的人数占总人数的一半,在回答“满意”的人中,“上班族”的人数是“非上班族”人数的;在回答“不满意”的人中,“非上班族”占.
(1)请根据以上数据填写下面列联表,并依据小概率值的独立性检验,分析能否认为市民对于交通的满意度与是否为上班族存关联?
满意 不满意 合计
上班族
非上班族
合计
(2)为了改善市民对交通状况的满意度,机构欲随机抽取部分市民做进一步调查.规定:抽样的次数不超过,若随机抽取的市民属于不满意群体,则抽样结束;若随机抽取的市民属于满意群体,则继续抽样,直到抽到不满意市民或抽样次数达到时,抽样结束.
(i)若,写出的分布列和数学期望;
(ii)请写出的数学期望的表达式(不需证明),根据你的理解说明的数学期望的实际意义.
附:
参考公式:,其中.
18.第24届冬季奥林匹克运动会将于2022年2月4日至20日在北京举行,践行“绿色奥运 科技奥运 人文奥运”理念,举办一届“有特色 高水平”的奥运会,是中国向世界的庄严承诺.为宣传北京冬奥会,某市开展了冬奥知识竞答活动.从参与的市民中随机抽取100人,统计他们的竞答成绩得到下面的列联表(单位:人).
成绩合格 成绩不合格 合计
男性 40 50
女性 20
合计
(1)完成列联表,并估计该市参与此次冬奥知识竞答的市民的成绩合格率;
(2)根据列联表判断是否有95%的把握认为该市参与此次冬奥知识竞答的市民的成绩与性别有关?
参考公式:
19.手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式.在某市随机调查了200名顾客购物时使用手机支付的情况,得到如下的2×2列联表.已知从使用手机支付的人群中随机抽取1人,抽到青年的概率为.
(1)根据已知条件完成2×2列联表,并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”?
2×2列联表:
青年 中老年 总计
使用手机支付 120
不使用手机支付 48
总计 200
(2)现采用分层抽样的方法从这200名顾客中按照“使用手机支付”和“不使用手机支付”抽取得到一个容量为5的样本,设事件A为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件A发生的概率.
附:,其中n=a+b+c+d,
P(K2≥k0) 0.05 0.025 0.010 0.005
k0 3.841 5.024 6.635 7.879
20.疫苗是指用各种病原微生物制作的用于预防接种的生物制品,接种疫苗是预防和控制传染病最经济 有效的公共卫生干预措施.某制药厂对预防某种疾病的两种疫苗开展临床对比试验.若使用后的抗体呈阳性,则认为疫苗有效.在已经接种疫苗的群体中随机抽取的100个样本,其中有60个接种了灭活疫苗,剩余40个接种了核酸疫苗.根据样本数据绘制等高条形图(如图所示),其中两个深色条的高分别表示接种灭活疫苗和核酸疫苗样本中抗体呈阳性的频率.现从这100个样本中随机抽取1人,已知事件“该样本接种了灭活疫苗且抗体呈阳性”发生的概率为0.54.
(1)求等高条形图中a的值;
(2)请在答题卷中完成下面的列联表,并判断能否在犯错概率不超过0.10的前提下认为两种疫苗的预防效果存在差异?
灭活疫苗 核酸疫苗 总计
抗体为阳性
抗体为阴性
总计 60 40 100
参考公式:,其中
0.15 0.10 0.01
2.072 2.706 6.635
21.“双减”政策明确指出要通过阅读等活动,充分用好课后服务时间,为学有余力的学生拓展学习空间.某家庭有小明和小红两个孩子,父母每天为他们安排了自由阅读的时间,约定周一到周日每天的阅读时间不能比前一天少.为了调查两人自由阅读时间的情况,父亲记录了两人某周每天的阅读时间(单位:min),如下表所示,其中小明周日的阅读时间a忘了记录,但知道,.
周一 周二 周三 周四 周五 周六 周日
序号x 1 2 3 4 5 6 7
小明的阅读时间y/min 16 20 20 25 30 36 a
小红的阅读时间z/min 16 22 25 26 32 35 35
(1)求小明这一周的阅读时间超过小红这一周的阅读时间的概率;
(2)根据小明这一周前6天的阅读时间,求其阅读时间y关于序号x的线性回归方程,并估计小明周日阅读时间a的值.
参考公式:回归方程中斜率与截距的最小二乘估计公式分别为,.
22.2021年春节前,受疫情影响,各地鼓励外来务工人员选择就地过年.某市统计了该市4个地区的外来务工人数与就地过年人数(单位:万),得到如下表格:
A区 B区 C区 D区
外来务工人数x/万 3 4 5 6
就地过年人数y/万 2.5 3 4 4.5
(1)请用相关系数说明y与x之间的关系可用线性回归模型拟合,并求关于的线性回归方程.
(2)假设该市政府对外来务工人员中选择就地过年的每人发放1000元补贴.
(i)若该市E区有2万名外来务工人员,根据(1)的结论估计该市政府需要给E区就地过年的人员发放的补贴总金额;
(ii)若A区的外来务工人员中甲 乙选择就地过年的概率分别为,,该市政府对甲 乙两人的补贴总金额的期望不超过1500元,求的取值范围.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据题目列出列联表,再根据列联表的数据计算值,进而得到关于的关系式,求解即可.
【详解】
由题可知,男女各人,列联表如下:
喜欢 不喜欢 总计
男 30m 20m 50m
女 20m 30m 50m
总计 50m 50m 100m
,
有99.9%把握认为性别与是否喜欢该学科有关,
,解得,
,
,
.
故选:B
2.B
【解析】
根据分层抽样以及频率分布直方图列联表,再计算,结合表中的数据判断即可.
【详解】
由频率分布直方图可知, 平均体育锻炼时间不少于4小时的频率为,故经常进行体育锻炼的学生人.又其中有40位女生的每周平均体育锻炼时间超过4小时,故有位男生经常锻炼.根据分层抽样的方法可知,样本中男生的人数为,女生有.列出列联表有:
男生 女生 总计
经常锻炼 110 40 150
不经常锻炼 30 20 50
总计 140 60 200
故,因为.
故有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”.
故选:B
【点睛】
本题主要考查了分层抽样以及频率分布直方图的运用,同时也考查了独立性检验在实际情景中的运用.属于中档题.
3.B
【解析】
【分析】
由已知求得,,代入求得a值,则线性回归方程可求,取求得y值即可.
【详解】
,,
,则线性回归方程为,
取,得.
故选:B.
【点睛】
本题考查线性回归方程,明确线性回归方程恒过样本点的中心是关键,是基础题.
4.D
【解析】
【分析】
设男生至少有人,根据条件,列出联表,计算出,令6.635,即可求出.
【详解】
设男生至少有人,根据题意,可列出如下联表:
喜欢数学文化 不喜欢数学文化 总计
男生
女生
总计
则,
若有的把握认为是否喜欢数学文化和性别有关,
则,即,
解得,
由于表中人数都为整数,所以,
即男生至少有18人.
故选:D.
【点睛】
本题考查独立性检验,属于基础题.
5.C
【解析】
【分析】
求出,代入方程检验,然后根据的变化趋势判系数的正负可得.
【详解】
由题意,,
把代入各方程,A中,,同理有B中,,C中,D中,,
又表格中数据随着的增大,减小,因此它们负相关,的系数为负.
故选:C.
【点睛】
在求线性回归方程时,可观察已知数据,呈线性相关的数据,如果随的增大,也增大,则与是正相关,在回归直线方程中的系数为正,反之为负.
6.A
【解析】
【分析】
根据列联表计算,对照临界值即可得出结论.
【详解】
根据列联表,计算,
由临界值表可知,
有95%的把握认为药物有效,A正确
故选:A
7.A
【解析】
【分析】
可设出缺少的数值,利用表中的数据,分别表示出、,将样本中心点带入回归方程,即可求得参数.
【详解】
设缺少的数值为,则,,
因为回归直线方程经过样本点的中心,所以,解得.
故选:A.
8.B
【解析】
【分析】
分别根据表中数据基础出四种函数模型的解析式,然后代入各解析式,计算出各模型在时的停车距离的估计值,然后和实验数据118进行比较,最接近的拟合效果最好.
【详解】
若选择模型①,则,解得,,
故,
当时,停车距离d的预测值为,
若选择模型②,则,解得,,
故,
当时,停车距离d的预测值为,
若选择模型③,则,解得,,
故,
当时,停车距离d的预测值为,
若选择模型④,则,解得,,
故,
当时,停车距离d的预测值为,
由实验数据可知当时,停车距离为,
故模型②的预测值更接近,故模型②拟合效果最好.
故选:B.
【点睛】
本题考查利用函数模型拟合变量间的相关关系,考查学生的计算能力,属于中档题.
9.BC
【解析】
【分析】
先求出样本中心点的坐标,再求出,即可判断得解.
【详解】
由题得,
,
所以.
所以.
当时,,所以选项B正确,选项A错误;
因为,
所以若年可支配收入每增加1万元,则年家庭消费相应平均增加0.5万元,
所以选项C正确,选项D错误.
故选:BC
【点睛】
本题主要考查线性回归方程的求法和应用,意在考查学生对这些知识的理解掌握水平,属于基础题.
10.AD
【解析】
【分析】
根据方差的计算公式,回归直线与回归方程的含义,独立性检验的概念判断各选项.
【详解】
解:A,将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;由于平均值增加相同的值,故A正确;
B,在回归直线方程中,当解释变量x每增加一个单位时,故预报变平均减少5个单位,故B不正确;
C,回归方程,可能不过散点中的任何一个点,故C不正确;
D.在列联表中,由计算得,对照临界值得,有99%的把握确认这两个变量间有关系,故D正确
故选:AD.
11.ACD
【解析】
【分析】
利用回归直线方程结合各选项的条件逐一分析计算即可判断作答.
【详解】
对于A,,由回归直线方程得,则,A正确;
对于B,由回归直线方程及数表知,具有正相关关系,而相关系数的绝对值不超过1,B不正确;
对于C,第三个样本点对应的残差,C正确;
对于D,在回归直线方程中,时,生产能耗约(吨) ,D正确.
故选:ACD
12.ABC
【解析】
【分析】
由题知,再结合题意依次讨论各选项即可得答案.
【详解】
解:因为,,
所以,,
所以对于A选项,的平均数为,故正确;
对于B选项,数据中的每个数都加上同一个常数,方差不变,故正确;
对与C选项,若数据的线性回归方程是,则,故正确;
对于D选项,当变量,的线性负相关时,相关系数越大,两个变量,的线性相关性越弱,故错误;
故选:ABC
13.0.05
【解析】
【详解】
分析:直接利用独立性检验公式计算即得解.
详解:由题得,
所以犯错误的概率最多不超过0.05的前提下,可认为“注射疫苗”与“感染流感”有关系.
故答案为0.05.
点睛:本题主要考查独立性检验和的计算,意在考查学生对这些知识的掌握水平和解决实际问题的能力.
14.5
【解析】
【详解】
分析:由题意求出样本中心点,然后求出新数据的样本中心,利用回归直线的斜率估计值为,求出新的回归方程,然后再计算时的值.
详解:∵一组数据确定的回归直线方程为,且,
∴,
解得,
∴原数据的样本中心点为(2,4).
由题意得去掉数据后新数据的样本中心为(2,4),重新求得的回归直线的斜率估计值为,
∴可设新的回归直线方程设为,
将点(2,4)代入上式后得,
解得,
∴新的回归直线的方程为,
将代入回归直线方程求得.
点睛:线性回归方程过样本中心点是重要的结论,利用此结论可求回归直线中的参数,也可求原样本数据中的参数.另外,根据线性回归方程可进行估计和预测.
15.①②③
【解析】
【详解】
①相关指数表示解释变量对于预报变量的贡献率,越接近于1,表示回归效果越好;是正确的;②两个变量相关性越强,则相关系数r的绝对值就越接近于1,是正确的;③在回归直线方程中,当解释变量每增加一个单位时,预报变量平均减少0.5个单位是正确的,因为回归方程,并不是样本点都落在方程上,故只能是估计值,所以说是平均增长;④对分类变量与,它们的随机变量的观测值来说,越小,“与有关系”的把握程度越小;故原命题错误;
故答案为①②③.
16.106
【解析】
【分析】
求出样本中心坐标,代入回归方程即可求出值.
【详解】
解:,,
将代入回归方程得,
解得.
故答案为:.
【点睛】
本题考查回归方程问题,属于基础题.
17.(1)列联表见解析,市民对交通的满意度与是否上班有关,此推断犯错误的概率不大于0.001
(2)(i)分布列见解析,;(ii),平均每抽取2个人,就会有一个不满意的市民
【解析】
【分析】
(1)根据题意完成列联表,进而利用公式计算可得,查表分析可得结果;
(2)(i)由(1)可知市民的满意度和不满意度均为,计算可得的分布列和数学期望,(ⅱ)由(i)可得,当n趋向于正无穷大时,趋向于2,即可理解为平均每抽取2个人,就会有一个不满意的市民.
(1)
由题意可知
满意 不满意 合计
上班族 15 40 55
非上班族 35 10 45
合计 50 50 100
零假设为:市民对交通的满意度与是否上班独立,
因为;
根据小概率值的独立性检验,我们推断不成立,即认为市民对交通的满意度与是否上班有关,此推断犯错误的概率不大于0.001.
(2)
(i)当时,的取值为1,2,3,4,5,
由(1)可知市民的满意度和不满意度均为;
所以,,,,,
所以的分布列为
1 2 3 4 5
P
所以;
(ⅱ)
当n趋向于正无穷大时,趋向于2,此时恰好为不满意度的倒数;
也可以理解为平均每抽取2个人,就会有一个不满意的市民.
18.(1)列联表答案见解析,估计该市参与此次冬奥知识竞答的市民的成绩合格率为0.7
(2)有95%的把握认为该市参与此次冬奥知识竞答的市民的成绩与性别有关
【解析】
【分析】
(1)根据题意完成列联表,进而可得该市参与此次冬奥知识竞答的市民的成绩合格率;
(2)利用卡方的计算公式求出观测值,与3.841比大小即可得出结果.
(1)
完成列联表(单位:人)
成绩合格 成绩不合格 合计
男性 40 10 50
女性 30 20 50
合计 70 30 100
由列联表,从参与的市民中随机抽取100人,有70人竞答成绩合格,
所以估计该市参与此次冬奥知识竞答的市民的成绩合格率为0.7.
(2)
由列联表,的观测值,
∴有95%的把握认为该市参与此次冬奥知识竞答的市民的成绩与性别有关.
19.(1)表格见解析,有
(2)
【解析】
【分析】
(1)根据抽到青年的概率为,得到使用手机支付的人群中的青年的人数和中老年的人数,完成2×2列联表,再求得K2的观测值,再与临界值表对照下结论;
(2)由分层抽样,得到使用手机支付的人数和不使用手机支付的人数,利用古典概型的概率求解.
(1)
解:∵从使用手机支付的人群中随机抽取1人,抽到青年的概率为,
∴使用手机支付的人群中的青年的人数为×120=84.
则使用手机支付的人群中的中老年的人数为120-84=36,
所以2×2列联表为:
青年 中老年 总计
使用手机支付 84 36 120
不使用手机支付 32 48 80
总计 116 84 200
K2的观测值k==≈17.734.
∵17.734>7.879,P(K2≥7.879)=0.005,
故有99.5%的把握认为“市场购物用手机支付与年龄有关”.
(2)
这200名顾客中采用分层抽样,从“使用手机支付”和“不使用手机支付”中抽到一个容量为5的样本中:
使用手机支付的人有5×=3人,记编号为1,2,3.
不使用手机支付的人有2人,记编号为a,b.
则从这个样本中任选2人有(1,2),(1,3),(1,a),(1,b),(2,3),(2,a),(2,b),(3,a),(3,b),(a,b)共10种.
其中至少有1人是不使用手机支付的有(1,a),(1,b),(2,a),(2,b),(3,a),(3,b),(a,b)共7种.
故所求事件A的概率P(A)=.
20.(1)
(2)列联表答案见解析,不能在犯错概率不超过0.10的前提下认为两种疫苗的预防效果存在差异
【解析】
【分析】
(1)根据题意得,解方程即可得答案;
(2)结合题意得接种灭活疫苗抗体阳性的共有人,接种核酸疫苗后抗体呈阳性的共有人,进而完成列联表,结合独立性检验求解即可.
(1)
解:依题意“1名受访者接种灭活疫苗且接种后抗体呈阳性”发生的概率为0.54,
所以
解得,所以
(2)
解:根据题意,接种灭活疫苗抗体阳性的共有:人,
接种核酸疫苗后抗体呈阳性的共有:人,
故列联表如下:
灭活疫苗 核酸疫苗 总计
抗体为阳性 54 34 88
抗体为阴性 6 6 12
总计 60 40 100
零假设为接种两种疫苗效果无差异
根据列联表中的数据,得到
因为
所以不能在犯错概率不超过0.10的前提下认为两种疫苗的预防效果存在差异.
21.(1);
(2),38.
【解析】
【分析】
(1)由,可得a的所有可能取值,计算出超过小红的阅读时间的a的可能取值即可计算作答.
(2)根据给定数表算出最小二乘估计公式中的相关量,再代入公式计算即可,并估计a的值.
(1)
依题意,,,则a的取值一共有25个不同结果,它们等可能,
令,解得,
因此,当小明这一周的阅读时间超过小红这一周的阅读时间时,a的取值一共有16个不同结果,
所以小明这一周的阅读时间超过小红这一周的阅读时间的概率为.
(2)
由数表得:,,
,,
所以,则,
所以y关于x的线性回归方程为,
当时,,
所以估计小明周日阅读时间a的值为38.
22.(1)说明答案见解析,
(2)(i)(万元);(ii)
【解析】
【分析】
(1)根据相关系数的绝对值越接近1,线性回归模型的拟合效果越好,即可以根据直接计算相关系数的值来判断与之间的线性相关程度的强弱;关于的线性回归方程直接用参考公式求解.
(2)(i)将代入(1)中的线性回归方程,即可求出E区就地过年的人数;
(ii)由X的所有可能取值为0,1,2,并分别求出相应的概率,即可得到分布列,然后求出期望,最后列出不等式求出的取值范围.
(1)
(1)由题,,,
,
,
,
所以相关系数,
因为y与x之间的相关系数近似为0.99,说明y与x之间的线性相关程度非常强,所以可用线性回归模型拟合y与x之间的关系.
,,
故y关于x的线性回归方程为.
(2)
(2)(i)将代入,得,
故估计该市政府需要给E区就地过年的人员发放的补贴总金额为(万元).
(ii)设甲 乙两人中选择就地过年的人数为X,则X的所有可能取值为0,1,2,
,
,
.
所以,
所以,
由,得,
又,所以,
故的取值范围为.
答案第1页,共2页
答案第1页,共2页
