高二下数学人教A版(2019)选择性必修第三册第七章随机变量及其分别单元检测卷(Word含解析)
文档属性
| 名称 | 高二下数学人教A版(2019)选择性必修第三册第七章随机变量及其分别单元检测卷(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 457.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 08:53:09 | ||
图片预览




文档简介
第七章随机变量及其分别单元检测卷
一、单选题
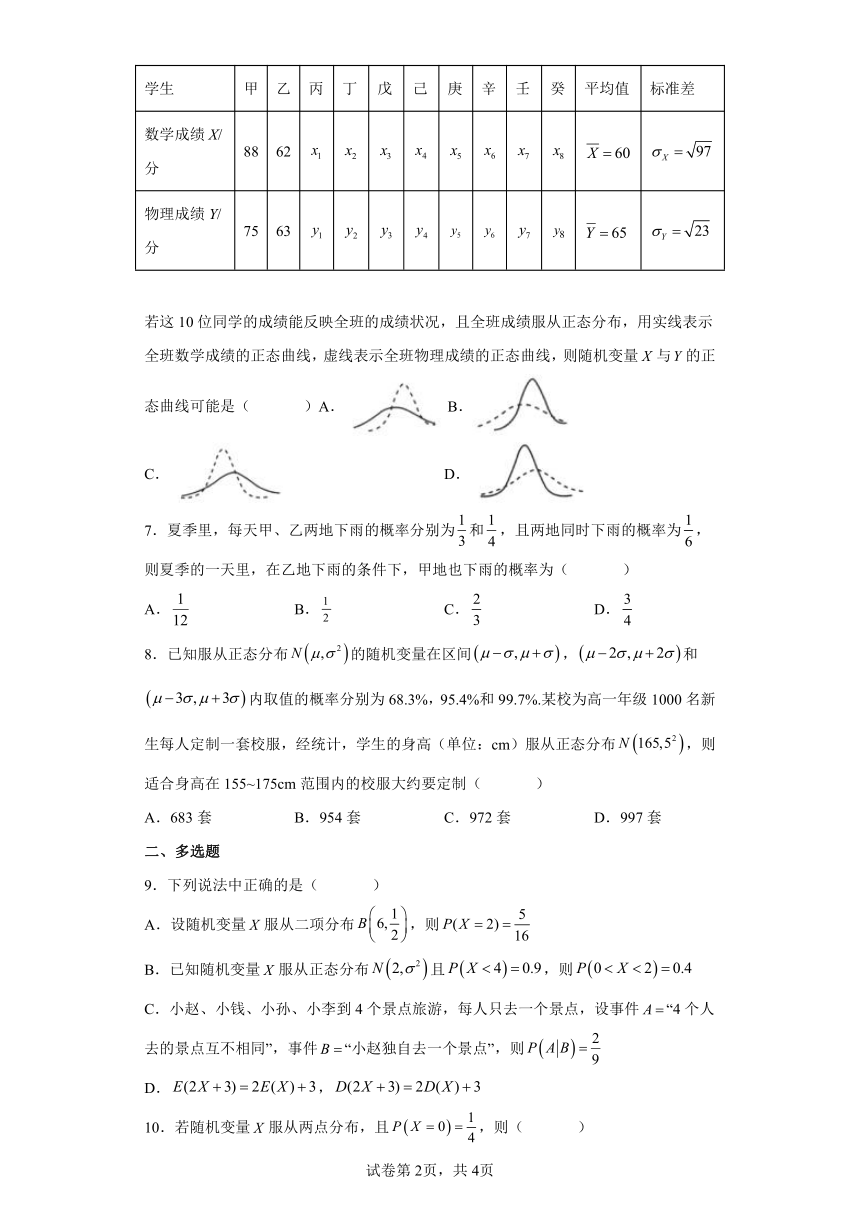
1.有一批同一型号的产品,已知其中由一厂生产的占30%,二厂生产的占50%,三厂生产的占20%.又知这三个厂的产品次品率分别为2%,1%,1%,则从这批产品中任取一件是次品的概率是( )
A.0.013 B.0.04 C.0.002 D.0.003
2.已知5%的男人和0.25%的女人患色盲,假如男人、女人各占一半,现随机选一人,则此人恰是色盲的概率是( )
A.0.012 45 B.0.057 86 C.0.026 25 D.0.028 65
3.王先生家住A小区,他工作在B科技园区,从家开车到公司上班路上有,两条路线(如图),路线上有,,三个路口,各路口遇到红灯的概率均为;路线上有,两个路口,各路口遇到红灯的概率依次为,.若分别走,路线,则王先生遇到红灯次数的数学期望分别为( )
A., B., C., D.,
4.甲、乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止,设甲在每局中获胜的概率为,乙在每局中获胜的概率为,且各局胜负相互独立,则比赛停止时已打局数ξ的期望E(ξ)为( )
A. B.
C. D.
5.已知随机变量,,则的值为( )
A.0.16 B.0.32 C.0.68 D.0.84
6.王老师为了了解全班50位同学某次考试的成绩状况,随机抽查了10位同学该次考试的数学与物理成绩,列表如下:
学生 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 平均值 标准差
数学成绩X/分 88 62
物理成绩Y/分 75 63
若这10位同学的成绩能反映全班的成绩状况,且全班成绩服从正态分布,用实线表示全班数学成绩的正态曲线,虚线表示全班物理成绩的正态曲线,则随机变量与的正态曲线可能是( )A. B.
C. D.
7.夏季里,每天甲、乙两地下雨的概率分别为和,且两地同时下雨的概率为,则夏季的一天里,在乙地下雨的条件下,甲地也下雨的概率为( )
A. B. C. D.
8.已知服从正态分布的随机变量在区间,和内取值的概率分别为68.3%,95.4%和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布,则适合身高在155~175cm范围内的校服大约要定制( )
A.683套 B.954套 C.972套 D.997套
二、多选题
9.下列说法中正确的是( )
A.设随机变量服从二项分布,则
B.已知随机变量服从正态分布且,则
C.小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件“4个人去的景点互不相同”,事件“小赵独自去一个景点”,则
D.,
10.若随机变量服从两点分布,且,则( )
A. B.
C. D.
11.下列说法中正确的有( )
A.将一组数据中的每个数据都乘以后,平均数也变为原来的倍
B.若一组数据的方差越小,则该组数据越稳定
C.由样本数据点、、、所得到的回归直线至少经过其中的一个点
D.在某项测量中,若测量结果,则
12.下列说法不正确的是( )
A.
B.是可能的
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.投掷两颗均匀的骰子,已知点数不同,设两颗骰子点数之和为X,则的概率为________.
14.东北育才高中部高一年级开设游泳、篮球和足球三门体育选修课,高一某班甲、乙、丙三名同学每人从中只选修一门课程.设事件A为“甲独自选修一门课程”,B为“三人选修的课程都不同”,则概率______.
15.已知随机变量的分布列为
-1 0 1
则随机变量的方差的值为______.
16.一袋中装有分别标记着,,数字的个小球,每次从袋中取出一个球(每只小球被取到的可能性相同),现连续取次球,若每次取出一个球后放回袋中,记次取出的球中标号最小的数字与最大的数字分别为,,设,则______ .
四、解答题
17.已知,判断A与B是否独立.
18.已知随机变量,查标准正态分布表,求:
(1);
(2);
(3);
(4);
(5).
19.李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时,样本方差为36;骑自行车平均用时,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有可用,李明应选择哪种交通工具?如果某天只有可用,又应该选择哪种交通工具?请说明理由.
20.已知,判断A与B是否独立.
21.已知10件产品中有3件是一等品,其余都是二等品,从这些产品中不放回地抽取两次,若已知第一次取到的是一等品,求第二次取到的也是一等品的概率.
22.假设每次测量中,出现正误差与负误差的概率都是0.5,设3次测量中,出现正误差的次数为X,写出X的分布列.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
设事件A为“任取一件为次品”,事件Bi为“任取一件为i厂的产品”,i=1,2,3,利用全概率公式P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)即得解
【详解】
设事件A为“任取一件为次品”,
事件Bi为“任取一件为i厂的产品”,i=1,2,3,
则Ω=B1∪B2∪B3,且B1,B2,B3两两互斥,
易知P(B1)=0.3,P(B2)=0.5,P(B3)=0.2,P(A|B1)=0.02,P(A|B2)=0.01,P(A|B3)=0.01.
∴P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)=0.02×0.3+0.01×0.5+0.01×0.2=0.013.
故选:A
2.C
【解析】
【分析】
【详解】
用事件A,B分别表示随机选一人是男人或女人,用事件C表示此人恰好患色盲,则Ω=A∪B,且A,B互斥,P(C)=P(A)P(C|A)+P(B)P(C|B)=×5%+×0.25%=0.026 25.
3.D
【解析】
【分析】
利用二项分布的期望公式求解走路线,王先生遇到红灯次数的数学期望;走路线:的可能取值为0,1,2,分别求出相应的概率,由此能求出走路线,王先生遇到红灯次数的数学期望.
【详解】
设王先生遇到红灯次数为随机变量X.
若走路线,X的取值范围为{0,1,2,3},且,所以;
若走路线,X的取值范围为{0,1,2},则由题意知,,,所以.
故选:D.
4.B
【解析】
【分析】
根据题意得到随机变量ξ的可能取值为,求得每两局比赛为一轮的概率为,进而求得相应的概率,利用期望的公式,即可求解.
【详解】
由题意,随机变量ξ的可能取值是,
设每两局比赛为一轮,则该轮比赛停止的概率为,
若该轮结束时比赛还要继续,则甲、乙在该轮中必是各得一分,
此时该轮比赛结果对下一轮比赛是否停止没有影响,
所以,
所以期望为:.
故选:B.
5.A
【解析】
【分析】
根据正态密度曲线的特征和曲线的性质得到曲线的对称轴为直线,.
【详解】
由,得正态密度曲线的对称轴为直线,
如上图,则.
故选:A.
6.A
【解析】
【分析】
根据、的大小关系可得对称轴的位置关系,根据、可得图象的瘦高、矮胖,进而可得正确选项.
【详解】
因为,所以随机变量的正态曲线的对称轴在随机变量的正态曲线的对称轴的左边,排除B,C;
因为,所以随机变量的总体分布更离散,正态曲线比随机变量的正态曲线“矮胖”,排除D,
故选:A.
7.C
【解析】
【分析】
记事件A为甲地下雨,事件B为乙地下雨,根据条件概率的公式计算即可得出结果.
【详解】
记事件A为甲地下雨,事件B为乙地下雨,
在乙地下雨的条件下,甲地也下雨的概率为.
故选:C
8.B
【解析】
【分析】
根据正态分布可得身高在155~175cm范围内的概率为95.4%,即可求出答案.
【详解】
因为学生的身高(单位:cm)服从正态分布,
所以身高在155~175cm范围内即在内取值,概率为95.4%,
所以身高在155~175cm范围内的校服大约要定制套.
故选:B.
9.BC
【解析】
【分析】
对于A,利用二项分布的概率公式求解判断;对于B,利用正态曲线的对称性求解;对于C,利用条件概率公式求解;对于D,利用期望和方差的性质判断
【详解】
解:对于A,因为随机变量服从二项分布,则,所以A错误,
对于B,随机变量服从正态分布且,所以,所以,所以B正确,
对于C,因为事件“4个人去的景点互不相同”,事件“小赵独自去一个景点”,所以由题意得,所以,所以C正确,
对于D,,,所以D错误,
故选:BC
10.AC
【解析】
【分析】
由两点分布性质可知,根据数学期望和方差计算公式可判断AC的正误;根据均值和方差的性质可判断BD的正误.
【详解】
随机变量服从两点分布且,.
对于A,,,A正确;
对于B,,B错误;
对于C,,C正确;
对于D,,D错误.
故选:AC.
11.ABD
【解析】
【分析】
利用平均数公式可判断A选项;利用方差的定义可判断B选项;利用回归直线的特点可判断C选项;利用正态密度曲线的对称性可判断D选项.
【详解】
对于A,设数据、、、的平均数为,则,
则数据、、、的平均数为,A对;
对于B,由方差的定义可知,方差越小,样本越稳定,B对;
对于C,回归直线一定过样本的中心点,不一定过样本点,C错;
对于D, 在某项测量中,若测量结果,则,D对.
故选:ABD.
12.ACD
【解析】
【分析】
根据条件概率公式及性质相关知识即可求解.
【详解】
由条件概率公式及知,故A错误;
当事件包含事件时,有,此时,故B正确;
由于,,故C,D错误.
故选:ACD.
13.
【解析】
【分析】
根据条件概率公式可直接求出答案.
【详解】
设A=“投掷两颗骰子,其点数不同”,B=“”,
则,P(AB)=,所以P(B|A)=.
故答案为:.
14.##
【解析】
【分析】
分别求出事件:A=“甲独自选修一门课程”,“甲独自选修一门课程且三人选修的课程都不同”对应的基本事件个数,然后套用条件概率公式求解.
【详解】
由题意知,甲独自选修一门,则有3门课程可选,乙、丙只能从剩余的两门课程中选择,可能性为.所以.
三人选修的课程各不相同的可能性为:,即.
故.
故答案为:##
15.
【解析】
【分析】
根据分布列的性质,求得,结合期望与方差的公式,即可求解.
【详解】
由分布列的性质,可得,解得,
可得,
所以.
故答案为:.
16.##
【解析】
【分析】
先求出的可能取值,再求出相应的概率,进而求出期望.
【详解】
的可能取值为0,1,2,连续取3次球,它的取法共有种,其中的取法共有3种,为111,222,333,其中有12种,为112,121,211,122,212,221,223,232,323,332,233,322,其中有12种,为113,123,311,321,312,213,231,131,133,311,331,313,因此它们的概率分别为,故.
故答案为:
17.独立
【解析】
【分析】
根据条件概率公式计算概率,然后判断.
【详解】
,
,所以,又,,
所以相互独立.
18.(1)0.997
(2)0.6915
(3)0.9332
(4)0.0209
(5)0.9753
【解析】
【分析】
对(1)(2)直接查表填写即可;对(3),;
对(4),;
对(5).
(1)
查表可知,;
(2)
查表可知,;
(3)
查表结合正态分布对称性,;
(4)
查表可知,;
(5)
查表可知,
.
19.(1),
(2)图象见解析
(3)自行车;公交车;理由见解析
【解析】
【分析】
(1)根据已知条件求得,从而求得正确答案.
(2)根据(1)画出和的分布密度曲线.
(3)根据(2)中的图象进行决策.
(1)
随机变量X的样本均值为30,样本标准差为6;随机变量Y的样本均值为34,样本标准差为2.用样本均值估计参数,用样本标准差估计参数,可以得到
;.
(2)
X和Y的分布密度曲线如图所示.
(3)
应选择在给定时间内不迟到的概率大的交通工具.由图可知,
,.
所以,如果有可用;那么骑自行车不迟到的概率大,应选择骑自行车;如果只有可用,那么坐公交车不迟到的概率大,应选择坐公交车.
20.A与B不相互独立
【解析】
【分析】
先由条件概率公式计算,判断是否成立,即可判断A与B是否独立.
【详解】
,
,即,
若A与B相互独立,则,
即,这与已知矛盾,
故A与B不相互独立.
21.
【解析】
【分析】
分别算出两次抽取中,第一次抽到一等品的抽法数和连续两次都抽到一等品的抽法数,代入公式计算即可.
【详解】
两次抽取中,第一次抽到一等品的抽法数为种,
连续两次都抽到一等品的抽法数为种,
故所求概率为.
22.见解析
【解析】
【分析】
利用二项分布直接求解
【详解】
由题意,X
,
,
,
故分布列为
X 0 1 2 3
P
答案第1页,共2页
答案第1页,共2页
一、单选题
1.有一批同一型号的产品,已知其中由一厂生产的占30%,二厂生产的占50%,三厂生产的占20%.又知这三个厂的产品次品率分别为2%,1%,1%,则从这批产品中任取一件是次品的概率是( )
A.0.013 B.0.04 C.0.002 D.0.003
2.已知5%的男人和0.25%的女人患色盲,假如男人、女人各占一半,现随机选一人,则此人恰是色盲的概率是( )
A.0.012 45 B.0.057 86 C.0.026 25 D.0.028 65
3.王先生家住A小区,他工作在B科技园区,从家开车到公司上班路上有,两条路线(如图),路线上有,,三个路口,各路口遇到红灯的概率均为;路线上有,两个路口,各路口遇到红灯的概率依次为,.若分别走,路线,则王先生遇到红灯次数的数学期望分别为( )
A., B., C., D.,
4.甲、乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止,设甲在每局中获胜的概率为,乙在每局中获胜的概率为,且各局胜负相互独立,则比赛停止时已打局数ξ的期望E(ξ)为( )
A. B.
C. D.
5.已知随机变量,,则的值为( )
A.0.16 B.0.32 C.0.68 D.0.84
6.王老师为了了解全班50位同学某次考试的成绩状况,随机抽查了10位同学该次考试的数学与物理成绩,列表如下:
学生 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 平均值 标准差
数学成绩X/分 88 62
物理成绩Y/分 75 63
若这10位同学的成绩能反映全班的成绩状况,且全班成绩服从正态分布,用实线表示全班数学成绩的正态曲线,虚线表示全班物理成绩的正态曲线,则随机变量与的正态曲线可能是( )A. B.
C. D.
7.夏季里,每天甲、乙两地下雨的概率分别为和,且两地同时下雨的概率为,则夏季的一天里,在乙地下雨的条件下,甲地也下雨的概率为( )
A. B. C. D.
8.已知服从正态分布的随机变量在区间,和内取值的概率分别为68.3%,95.4%和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布,则适合身高在155~175cm范围内的校服大约要定制( )
A.683套 B.954套 C.972套 D.997套
二、多选题
9.下列说法中正确的是( )
A.设随机变量服从二项分布,则
B.已知随机变量服从正态分布且,则
C.小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件“4个人去的景点互不相同”,事件“小赵独自去一个景点”,则
D.,
10.若随机变量服从两点分布,且,则( )
A. B.
C. D.
11.下列说法中正确的有( )
A.将一组数据中的每个数据都乘以后,平均数也变为原来的倍
B.若一组数据的方差越小,则该组数据越稳定
C.由样本数据点、、、所得到的回归直线至少经过其中的一个点
D.在某项测量中,若测量结果,则
12.下列说法不正确的是( )
A.
B.是可能的
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.投掷两颗均匀的骰子,已知点数不同,设两颗骰子点数之和为X,则的概率为________.
14.东北育才高中部高一年级开设游泳、篮球和足球三门体育选修课,高一某班甲、乙、丙三名同学每人从中只选修一门课程.设事件A为“甲独自选修一门课程”,B为“三人选修的课程都不同”,则概率______.
15.已知随机变量的分布列为
-1 0 1
则随机变量的方差的值为______.
16.一袋中装有分别标记着,,数字的个小球,每次从袋中取出一个球(每只小球被取到的可能性相同),现连续取次球,若每次取出一个球后放回袋中,记次取出的球中标号最小的数字与最大的数字分别为,,设,则______ .
四、解答题
17.已知,判断A与B是否独立.
18.已知随机变量,查标准正态分布表,求:
(1);
(2);
(3);
(4);
(5).
19.李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时,样本方差为36;骑自行车平均用时,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有可用,李明应选择哪种交通工具?如果某天只有可用,又应该选择哪种交通工具?请说明理由.
20.已知,判断A与B是否独立.
21.已知10件产品中有3件是一等品,其余都是二等品,从这些产品中不放回地抽取两次,若已知第一次取到的是一等品,求第二次取到的也是一等品的概率.
22.假设每次测量中,出现正误差与负误差的概率都是0.5,设3次测量中,出现正误差的次数为X,写出X的分布列.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【分析】
设事件A为“任取一件为次品”,事件Bi为“任取一件为i厂的产品”,i=1,2,3,利用全概率公式P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)即得解
【详解】
设事件A为“任取一件为次品”,
事件Bi为“任取一件为i厂的产品”,i=1,2,3,
则Ω=B1∪B2∪B3,且B1,B2,B3两两互斥,
易知P(B1)=0.3,P(B2)=0.5,P(B3)=0.2,P(A|B1)=0.02,P(A|B2)=0.01,P(A|B3)=0.01.
∴P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)=0.02×0.3+0.01×0.5+0.01×0.2=0.013.
故选:A
2.C
【解析】
【分析】
【详解】
用事件A,B分别表示随机选一人是男人或女人,用事件C表示此人恰好患色盲,则Ω=A∪B,且A,B互斥,P(C)=P(A)P(C|A)+P(B)P(C|B)=×5%+×0.25%=0.026 25.
3.D
【解析】
【分析】
利用二项分布的期望公式求解走路线,王先生遇到红灯次数的数学期望;走路线:的可能取值为0,1,2,分别求出相应的概率,由此能求出走路线,王先生遇到红灯次数的数学期望.
【详解】
设王先生遇到红灯次数为随机变量X.
若走路线,X的取值范围为{0,1,2,3},且,所以;
若走路线,X的取值范围为{0,1,2},则由题意知,,,所以.
故选:D.
4.B
【解析】
【分析】
根据题意得到随机变量ξ的可能取值为,求得每两局比赛为一轮的概率为,进而求得相应的概率,利用期望的公式,即可求解.
【详解】
由题意,随机变量ξ的可能取值是,
设每两局比赛为一轮,则该轮比赛停止的概率为,
若该轮结束时比赛还要继续,则甲、乙在该轮中必是各得一分,
此时该轮比赛结果对下一轮比赛是否停止没有影响,
所以,
所以期望为:.
故选:B.
5.A
【解析】
【分析】
根据正态密度曲线的特征和曲线的性质得到曲线的对称轴为直线,.
【详解】
由,得正态密度曲线的对称轴为直线,
如上图,则.
故选:A.
6.A
【解析】
【分析】
根据、的大小关系可得对称轴的位置关系,根据、可得图象的瘦高、矮胖,进而可得正确选项.
【详解】
因为,所以随机变量的正态曲线的对称轴在随机变量的正态曲线的对称轴的左边,排除B,C;
因为,所以随机变量的总体分布更离散,正态曲线比随机变量的正态曲线“矮胖”,排除D,
故选:A.
7.C
【解析】
【分析】
记事件A为甲地下雨,事件B为乙地下雨,根据条件概率的公式计算即可得出结果.
【详解】
记事件A为甲地下雨,事件B为乙地下雨,
在乙地下雨的条件下,甲地也下雨的概率为.
故选:C
8.B
【解析】
【分析】
根据正态分布可得身高在155~175cm范围内的概率为95.4%,即可求出答案.
【详解】
因为学生的身高(单位:cm)服从正态分布,
所以身高在155~175cm范围内即在内取值,概率为95.4%,
所以身高在155~175cm范围内的校服大约要定制套.
故选:B.
9.BC
【解析】
【分析】
对于A,利用二项分布的概率公式求解判断;对于B,利用正态曲线的对称性求解;对于C,利用条件概率公式求解;对于D,利用期望和方差的性质判断
【详解】
解:对于A,因为随机变量服从二项分布,则,所以A错误,
对于B,随机变量服从正态分布且,所以,所以,所以B正确,
对于C,因为事件“4个人去的景点互不相同”,事件“小赵独自去一个景点”,所以由题意得,所以,所以C正确,
对于D,,,所以D错误,
故选:BC
10.AC
【解析】
【分析】
由两点分布性质可知,根据数学期望和方差计算公式可判断AC的正误;根据均值和方差的性质可判断BD的正误.
【详解】
随机变量服从两点分布且,.
对于A,,,A正确;
对于B,,B错误;
对于C,,C正确;
对于D,,D错误.
故选:AC.
11.ABD
【解析】
【分析】
利用平均数公式可判断A选项;利用方差的定义可判断B选项;利用回归直线的特点可判断C选项;利用正态密度曲线的对称性可判断D选项.
【详解】
对于A,设数据、、、的平均数为,则,
则数据、、、的平均数为,A对;
对于B,由方差的定义可知,方差越小,样本越稳定,B对;
对于C,回归直线一定过样本的中心点,不一定过样本点,C错;
对于D, 在某项测量中,若测量结果,则,D对.
故选:ABD.
12.ACD
【解析】
【分析】
根据条件概率公式及性质相关知识即可求解.
【详解】
由条件概率公式及知,故A错误;
当事件包含事件时,有,此时,故B正确;
由于,,故C,D错误.
故选:ACD.
13.
【解析】
【分析】
根据条件概率公式可直接求出答案.
【详解】
设A=“投掷两颗骰子,其点数不同”,B=“”,
则,P(AB)=,所以P(B|A)=.
故答案为:.
14.##
【解析】
【分析】
分别求出事件:A=“甲独自选修一门课程”,“甲独自选修一门课程且三人选修的课程都不同”对应的基本事件个数,然后套用条件概率公式求解.
【详解】
由题意知,甲独自选修一门,则有3门课程可选,乙、丙只能从剩余的两门课程中选择,可能性为.所以.
三人选修的课程各不相同的可能性为:,即.
故.
故答案为:##
15.
【解析】
【分析】
根据分布列的性质,求得,结合期望与方差的公式,即可求解.
【详解】
由分布列的性质,可得,解得,
可得,
所以.
故答案为:.
16.##
【解析】
【分析】
先求出的可能取值,再求出相应的概率,进而求出期望.
【详解】
的可能取值为0,1,2,连续取3次球,它的取法共有种,其中的取法共有3种,为111,222,333,其中有12种,为112,121,211,122,212,221,223,232,323,332,233,322,其中有12种,为113,123,311,321,312,213,231,131,133,311,331,313,因此它们的概率分别为,故.
故答案为:
17.独立
【解析】
【分析】
根据条件概率公式计算概率,然后判断.
【详解】
,
,所以,又,,
所以相互独立.
18.(1)0.997
(2)0.6915
(3)0.9332
(4)0.0209
(5)0.9753
【解析】
【分析】
对(1)(2)直接查表填写即可;对(3),;
对(4),;
对(5).
(1)
查表可知,;
(2)
查表可知,;
(3)
查表结合正态分布对称性,;
(4)
查表可知,;
(5)
查表可知,
.
19.(1),
(2)图象见解析
(3)自行车;公交车;理由见解析
【解析】
【分析】
(1)根据已知条件求得,从而求得正确答案.
(2)根据(1)画出和的分布密度曲线.
(3)根据(2)中的图象进行决策.
(1)
随机变量X的样本均值为30,样本标准差为6;随机变量Y的样本均值为34,样本标准差为2.用样本均值估计参数,用样本标准差估计参数,可以得到
;.
(2)
X和Y的分布密度曲线如图所示.
(3)
应选择在给定时间内不迟到的概率大的交通工具.由图可知,
,.
所以,如果有可用;那么骑自行车不迟到的概率大,应选择骑自行车;如果只有可用,那么坐公交车不迟到的概率大,应选择坐公交车.
20.A与B不相互独立
【解析】
【分析】
先由条件概率公式计算,判断是否成立,即可判断A与B是否独立.
【详解】
,
,即,
若A与B相互独立,则,
即,这与已知矛盾,
故A与B不相互独立.
21.
【解析】
【分析】
分别算出两次抽取中,第一次抽到一等品的抽法数和连续两次都抽到一等品的抽法数,代入公式计算即可.
【详解】
两次抽取中,第一次抽到一等品的抽法数为种,
连续两次都抽到一等品的抽法数为种,
故所求概率为.
22.见解析
【解析】
【分析】
利用二项分布直接求解
【详解】
由题意,X
,
,
,
故分布列为
X 0 1 2 3
P
答案第1页,共2页
答案第1页,共2页
