高一下数学人教A版(2019)第十章概率单元检测卷(Word含解析)
文档属性
| 名称 | 高一下数学人教A版(2019)第十章概率单元检测卷(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 539.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 09:05:02 | ||
图片预览



文档简介
第十章概率单元检测卷
一、单选题
1.从编号分别为,,,,的五个大小完全相同的小球中,随机取出三个小球,则恰有两个小球编号相邻的概率为( )
A. B. C. D.
2.某班新学期开学统计新冠疫苗接种情况,已知该班有学生45人,其中未完成疫苗接种的有5人,则该班同学的疫苗接种完成率为( )
A. B. C. D.
3.某产品分为甲、乙、丙三级,其中甲级为正品,乙、丙两级均属次品.从等级分别为甲、乙、丙的三件产品中任取一件,抽到甲、乙、丙三级产品分别为事件A, B, C,则抽得次品为( )
A.A B.
C. D.
4.某工厂有甲、乙、丙三名工人进行零件安装比赛,甲每个零件的安装完成时间少于丙的概率为.乙每个零件的安装完成时间少于丙的概率为,比赛要求甲、乙、丙各安装一个零件,且他们安装每个零件相互独立,则甲和乙中至少有一人安装完成时间少于丙的概率为( )
A. B. C. D.
5.甲、乙两名运动员各自等可能地从编号为、、的张卡片中选择张,则他们选择的卡片上的数字之和能被整除的概率为( )
A. B. C. D.
6.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上一面的点数是3”为事件B,则事件A,B中至少有一个发生的概率是( )
A. B. C. D.
7.费马小定理:若是质数,且,互质,那么的次方除以所得的余数恒等于1.依此定理,若在数集中任取两个数,其中一个作为,另一个作为,则所取的两个数符合费马小定理的概率为( )
A. B. C. D.
8.不透明的口袋内装有红色 绿色和蓝色小球各2个,一次任意摸出2个小球,则与事件“2个小球都为红色”互斥而不对立的事件有( )
A.2个小球不全为红色 B.2个小球恰有一个红色
C.2个小球至少有一个红色 D.2个小球不全为绿色
二、多选题
9.不透明的口袋内装有红色 绿色和蓝色卡片各2张,一次任意取出2张卡片,则与事件“2张卡片都为红色”互斥而不对立的事件有( )
A.2张卡片都不是红色 B.2张卡片恰有一张红色
C.2张卡片至少有一张红色 D.2张卡片都为绿色
10.连掷一枚均匀的骰子两次,所得向上的点数分别为a,b,记,则下列说法错误的是( )
A.事件“”的概率为
B.事件“”的概率为
C.事件“”与“”互为对立事件
D.事件“m是奇数”与“”互为互斥事件
11.某展会安排了分别标有序号为“号”“号”“号”的三辆车,等可能的随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计了两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“号”车的概率分别为,则( )
A. B. C. D.
12.甲、乙两人下棋,甲获胜的概率为,甲不输的概率为,下列说法正确的是( )
A.和棋的概率是 B.乙不输的概率是
C.乙胜的概率是 D.甲输的概率是
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘.10天后,又从池塘内捞出60条鱼,其中有标记的有2条.根据以上数据可以估计该池塘内共有___________条鱼.
14.下列试验是古典概型的为______.
①从6名同学中选出4人参加数学竞赛,每人被选中的可能性大小;
②同时掷两枚骰子,点数和为6的概率;
③近三天中有一天降雨的概率;
④甲乙等10人站成一排,其中甲、乙相邻的概率.
15.小张,小李,小王三位同学之间相互传球,假设他们相互间传球是等可能的,并且由小张开始传球,则经过5次传球后,球仍回到小张手中的概率为________.
16.小华、小明、小李小章去A,B,C三个工厂参加社会实践,要求每个工厂都有人去,且这四人都在这三个工厂实践,则小华和小李都没去B工厂的概率是________.
四、解答题
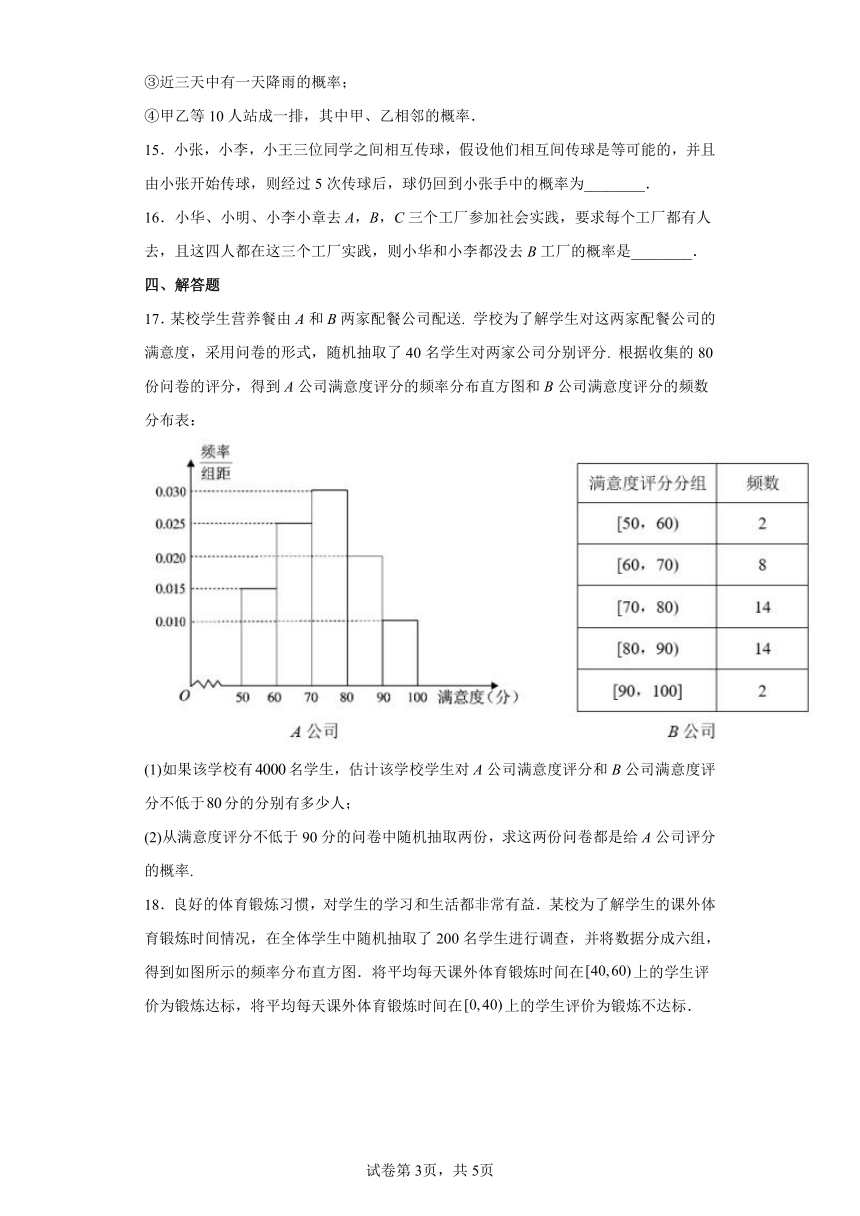
17.某校学生营养餐由A和B两家配餐公司配送. 学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分. 根据收集的80份问卷的评分,得到A公司满意度评分的频率分布直方图和B公司满意度评分的频数分布表:
(1)如果该学校有名学生,估计该学校学生对A公司满意度评分和B公司满意度评分不低于分的分别有多少人;
(2)从满意度评分不低于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率.
18.良好的体育锻炼习惯,对学生的学习和生活都非常有益.某校为了解学生的课外体育锻炼时间情况,在全体学生中随机抽取了200名学生进行调查,并将数据分成六组,得到如图所示的频率分布直方图.将平均每天课外体育锻炼时间在上的学生评价为锻炼达标,将平均每天课外体育锻炼时间在上的学生评价为锻炼不达标.
(1)估计这200名学生每天课外体育锻炼时间的第50百分位数与平均值(同一组中的数据用该组区间的中点值为代表);
(2)在上述锻炼达标的学生中按分层抽样的方法抽取8名,再从这8名同学中随机抽取2名,求这两名同学中至少有一名每天体育锻炼时间在的概率.
19.某花店每天以每枝元的价格从农场购进若干枝玫瑰花,然后以每枝元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(1)若花店一天购进枝玫瑰花,求当天的利润(单位:元)关于当天需求量(单位:枝,)的函数解析式.
(2)花店记录了天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n 14 15 16 17 18 19 20
频数 10 20 16 16 15 13 10
(i)假设花店在这天内每天购进枝玫瑰花,求这天的日利润(单位:元)的平均数;
(ii)若花店一天购进枝玫瑰花,以天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于元的概率.
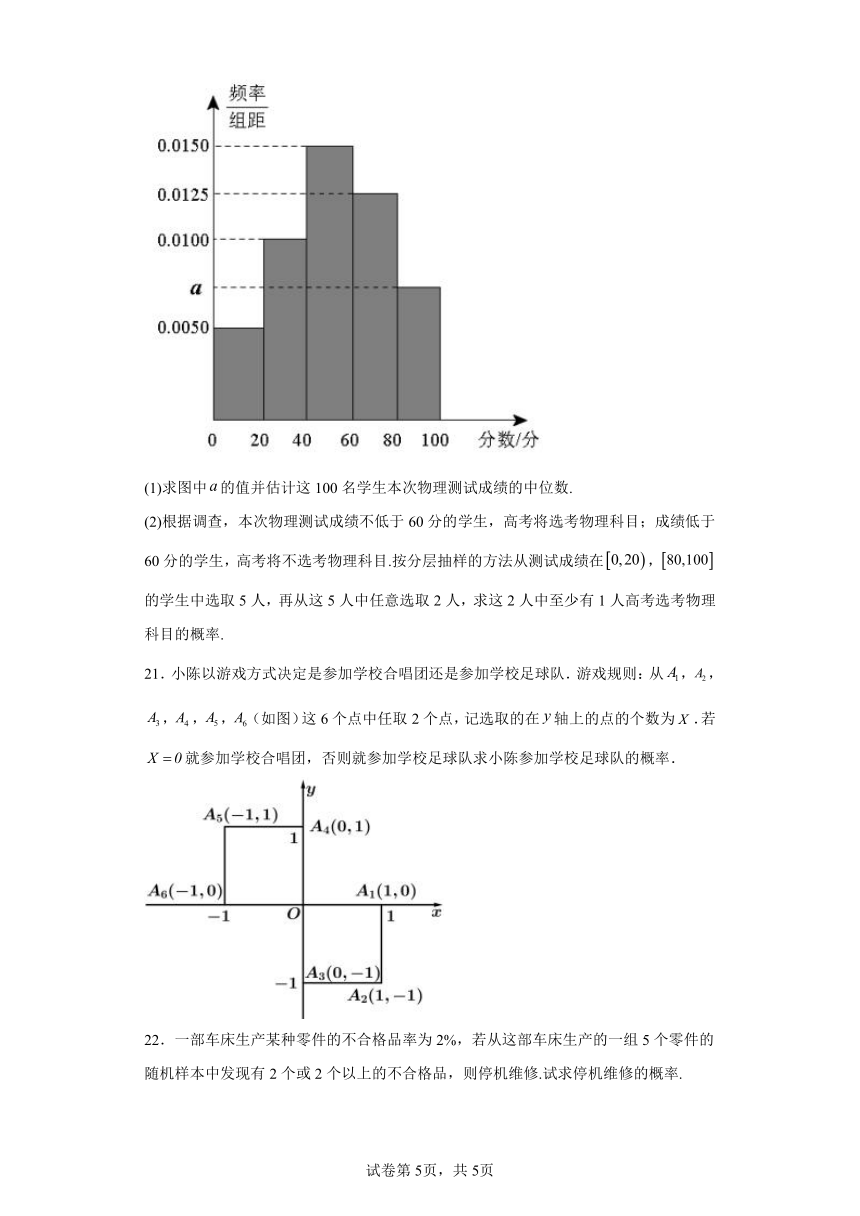
20.新高考取消文理分科,采用选科模式,这赋予了学生充分的自由选择权.新高考地区某校为了解本校高一年级将来高考选考物理的情况,随机选取了100名高一学生,将他们某次物理测试成绩(满分100分)按照,,,,分成5组,制成如图所示的频率分布直方图.
(1)求图中的值并估计这100名学生本次物理测试成绩的中位数.
(2)根据调查,本次物理测试成绩不低于60分的学生,高考将选考物理科目;成绩低于60分的学生,高考将不选考物理科目.按分层抽样的方法从测试成绩在,的学生中选取5人,再从这5人中任意选取2人,求这2人中至少有1人高考选考物理科目的概率.
21.小陈以游戏方式决定是参加学校合唱团还是参加学校足球队.游戏规则:从,,,,,(如图)这6个点中任取2个点,记选取的在轴上的点的个数为.若就参加学校合唱团,否则就参加学校足球队求小陈参加学校足球队的概率.
22.一部车床生产某种零件的不合格品率为2%,若从这部车床生产的一组5个零件的随机样本中发现有2个或2个以上的不合格品,则停机维修.试求停机维修的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
利用古典概型计算公式计算即可
【详解】
从编号分别为,,,,的五个大小完全相同的小球中,随机取出三个小球
共有种不同的取法,
恰好有两个小球编号相邻的有:
,共有6种
所以概率为
故选:C
2.D
【解析】
【分析】
利用古典概型的概率求解.
【详解】
该班同学的疫苗接种完成率为.
故选:D
3.D
【解析】
【分析】
根据事件的运算逐个判断即可.
【详解】
事件A为抽到一件正品,故A错误.
事件为抽到乙的反面,即抽到正品,故B错误.
事件为抽到丙的反面,即抽到正品,故C错误.
事件为抽取甲级产品的反面,即抽到次品,故D正确.
故选:D.
4.C
【解析】
【分析】
由独立事件概率乘法公式可求得甲和乙安装完成时间均多于丙的概率,由对立事件概率公式可求得结果.
【详解】
甲和乙安装完成时间均多于丙的概率为,
甲和乙中至少有一人安装完成时间少于丙的概率为.
故选:C.
5.A
【解析】
【分析】
利用古典概型的概率公式即求.
【详解】
由题知甲、乙两名运动员选择的卡片结果有:
共9种;
其中他们选择的卡片上的数字之和能被整除的有:共3种.
故他们选择的卡片上的数字之和能被整除的概率为.
故选:A
6.C
【解析】
【分析】
正难则反,先计算出事件A,B都不发生的概率,用1减去对应概率即可.
【详解】
由题可知,,则事件A,B都不发生的概率为,故事件A,B中至少有一个发生的概率是.
故选:C
7.A
【解析】
【分析】
利用古典概型的概率求解.
【详解】
样本点表示,,余类推,则样本空间,共有12个样本点.
记事件表示“所取的两个数符合费马小定理”,则事件所含的样本点为,,,,,,,共7个.
所以所取的两个数符合费马小定理的概率.
故选:A.
8.B
【解析】
【分析】
对于A两个事件是对立的事件,故A错误;对于B,两个事件是互斥而不对立的,故B正确;对于C,两个事件不是互斥事件,故C错误;对于D,两个事件可以同时发生,不互斥,故D也错误.
【详解】
一个口袋内装有大小、形状相同的红色、绿色和蓝色小球各2个,一次任意取出2个小球,
对于A,2个小球不全为红球与事件“2个小球都为红色”是对立的事件,故A错误;
对于B,2个小球恰有1个红球与事件“2个小球都为红色”互斥而不对立的事件,故B正确;
对于C,2个小球至少有1个红球与事件“2个小球都为红色”能同时发生,不是互斥事件,故C错误;
对于D,2个小球不全为绿球与事件“2个小球都为红色”是可以同时发生的事件,不是互斥事件,故D错误.
故选:B.
9.ABD
【解析】
【分析】
列举出所有情况,然后再利用互斥事件和对立事件的定义判断.
【详解】
解:6张卡片中一次取出张卡片的所有情况有:
“2张都为红色” “2张都为绿色” “2张都为蓝色” “1张为红色1张为绿色” “1张为红色1张为蓝色” “1张为绿色1张为蓝色”,
选项中给出的四个事件中与“2张都为红色”互斥而非对立的事件是:“2张都不是红色”,“2张恰有一张红色”,“2张都为绿色”,
其中“2张至少一张为红色”包含事件“2张都为红色”,二者并非互斥.
故选:ABD.
10.ABC
【解析】
【分析】
利用列举法和概率公式计算可知,AB错误,根据互斥、对立事件的概念可知,C错误,D正确.
【详解】
连掷一枚均匀的骰子两次,所得向上的点数有:,,,,,,共36种,
事件“”所包含的基本事件有:共1个,所以事件“”的概率为,故A错误;事件“” 所包含的基本事件有:,共1个,所以事件“”的概率为,故B错误;
事件“”与“”可以同时发生,不是对立事件,故C错误;
事件“m是奇数”与“”不能同时发生,所以事件“m是奇数”与“”互为互斥事件,故D正确.
故选:ABC
11.ACD
【解析】
【分析】
利用列举法求出方案一坐到“3号”车的概率,利用古典摡型求出方案二坐到“3号”车的概率,即可得到答案.
【详解】
由题意,分别标有序号为“1号”“2号”“3号”的三辆车,等坑随机顺序前往酒店接嘉宾,
基本事件有:,共6种,
设计两种方案:方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车,
则方案一坐到“3号”车包含的基本事件有:,共有3种,
所以方案一的概率为;
方案二:直接乘坐第一辆车,则方案二坐到“号”车的概率为,
所以.
故选:ACD .
12.ABD
【解析】
【分析】
利用互斥事件、对立事件的概率公式计算出各选项中事件的概率,由此可判断各选项的正误.
【详解】
对于A选项,和棋的概率是,A对;
对于B选项,乙不输的概率是,B对;
对于C选项,乙胜的概率是,C错;
对于D选项,甲输的概率是,D对.
故选:ABD.
13.900
【解析】
【分析】
估计该池塘内共有n条鱼,利用等可能事件概率计算公式列方程,能求出n的值.
【详解】
解:估计该池塘内共有n条鱼,
则,
解得n=900.
故答案为:900.
14.①②④
【解析】
【分析】
根据古典概型的特点,结合每个选项进行逐一分析,即可判断和选择.
【详解】
因为古典概型需要满足基本事件是有限个,且每个基本事件的概率相等,
据此①②④均符合要求,③不满足等可能的要求,因为降雨受多方面因素影响.
故答案为:①②④.
15.##0.3125
【解析】
【分析】
画出树状图列出基本事件再计算概率即可.
【详解】
根据题意,列出树状图如下:
由树状图可知,5次传球后的基本事件总数为32,球回到小张手中的基本事件数为10.
所以5次传球后球仍回到小张手中的概率为.
故答案为:.
16.
【解析】
【分析】
求出总的分配方法数,再按去1人或2人分类求得小华和小李都没去B工厂的方法数,然后由概率公式计算.
【详解】
由题意可知总的分配情况有种,其中满足条件的情况有种,故所求概率.
故答案为:.
17.(1)对A公司满意度评分不低于分的有人,对B公司满意度评分不低于分的有人;
(2).
【解析】
【分析】
(1)利用频率分布直方图可知A公司满意度评分不低于80分的频率,利用B公司满意度评分的频数分布表可知40人中不低于80分的频数,即求;
(2)利用列举法解决古典概型概率问题.
(1)
由A公司满意度评分的频率分布直方图可知不低于80分的频率为,
所以估计该校学生对A公司满意度评分不低于分的有人;
由B公司满意度评分的频数分布表可知40人中不低于80分的频数为,
频率为,
所以估计该校学生对B公司满意度评分不低于分的有人.
(2)
满意度不低于90分的问卷共有6份,其中4份评价公司,设为,2份评价B公司,设为,
从这6份问卷中随机取2份,样本空间,,,,,,,,,,,,,,}共有15种,
设两份问卷均是评价A公司为事件C,则C={,,,,,}共有6种,
则有,
所以这两份问卷都是给A公司评分的概率为.
18.(1)28.125,28.7;
(2)﹒
【解析】
【分析】
(1)根据已知条件,结合百分位数和平均值公式,即可求解;
(2)根据题意,求出从这8名同学中随机抽取2名的抽取方法数量m,求出这两名同学中没有一名每天体育锻炼时间在的抽取方法n,则所求概率为.
(1)
∵前2组频率为0.08+0.16=0.24,前三组的频率为0.24+0.32=0.56,∴第50百分位数在第3组,设第50百分位数为m,则,解得,
平均数为;
(2)
根据题意可得,从这8名同学中随机抽取2名,共有种不同的抽取方法,
抽取的8名同学中,每天体育锻炼时间在的有6名,每天体育锻炼时间在的有2名,这两名同学中没有一名每天体育锻炼时间在的抽取方法有种,∴这两名同学中至少有一名每天体育锻炼时间在的抽取方法有种,故所求概率为
19.(1);
(2)(i);(ii)
【解析】
【分析】
(1)根据卖出一枝可得利润5元,卖不出一枝赔本5元,即可建立分段函数;
(2)根据题意求得天所有的利润,除以即得每日利润;
(3)根据(2)中所求每日利润,结合利润不少于元的要求,将对应频率相加即可.
(1)
当需求量时,每日利润元;
当需求量时,每日利润元;
故每日利润关于的函数为:
(2)
(i)根据题意,天内,
有天的利润为元,有天的利润为元,
有天的利润为元,有天的利润为元,
故这天内,日利润的平均值为:元.
(ii)显然要满足题意,只需每日需求量即可.
故当天的利润不少于元的概率为:.
20.(1),中位数为;
(2).
【解析】
【分析】
(1)由频率和为1求参数a,根据直方图及中位数的性质求中位数即可.
(2)首先由分层抽样原则求选取的5人在、的人数分布情况,再应用列举法求古典概型的概率即可.
(1)
由图知:,解得.
学生成绩在的频率为;
学生成绩在的频率为.
设这100名学生本次物理测试成绩的中位数为,则,解得,
故估计这100名学生本次物理测试成绩的中位数为.
(2)
由(1)知,学生成绩在的频数为,学生成绩在的频数为.
按分层抽样的方法从中选取5人,则成绩在的学生被抽取人,分别记为,,成绩在的学生被抽取人,分别记为,,.
从中任意选取2人,有,,,,,,,,,这10种选法,
其中至少有1人高考选考物理科目的选法有,,,,,,,,这9种,
∴这2人中至少有1人高考选考物理科目的概率.
21.
【解析】
【分析】
根据古典概型公式,结合列举法、对立事件的概率公式进行求解即可.
【详解】
从,,,,,中任取2个点包含的所有情况为,,,,,,,,,,,,,,,共有15种,当时,所取的2个点均不在轴上,即从,,,中任取2个点,所有可能的情况为,,,,,,共6种,
所以小陈参加学校合唱团的概率为,
所以小陈参加学校足球队的概率.
22.0.004.
【解析】
【分析】
利用对立事件概率计算公式和次独立重复试验中事件恰好发生次的概率计算公式直接求解.
【详解】
一部车床生产某种零件的不合格品率为,合格的概率为,
事件:5个零件的随机样本中发现有2个或2个以上的不合格品,
事件:5个零件的随机样本中都合格或只有一个不合格,
根据独立重复事件的概率公式:
根据对立事件的概率公式:,
综上所述,结论是:停机维修的概率约为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.从编号分别为,,,,的五个大小完全相同的小球中,随机取出三个小球,则恰有两个小球编号相邻的概率为( )
A. B. C. D.
2.某班新学期开学统计新冠疫苗接种情况,已知该班有学生45人,其中未完成疫苗接种的有5人,则该班同学的疫苗接种完成率为( )
A. B. C. D.
3.某产品分为甲、乙、丙三级,其中甲级为正品,乙、丙两级均属次品.从等级分别为甲、乙、丙的三件产品中任取一件,抽到甲、乙、丙三级产品分别为事件A, B, C,则抽得次品为( )
A.A B.
C. D.
4.某工厂有甲、乙、丙三名工人进行零件安装比赛,甲每个零件的安装完成时间少于丙的概率为.乙每个零件的安装完成时间少于丙的概率为,比赛要求甲、乙、丙各安装一个零件,且他们安装每个零件相互独立,则甲和乙中至少有一人安装完成时间少于丙的概率为( )
A. B. C. D.
5.甲、乙两名运动员各自等可能地从编号为、、的张卡片中选择张,则他们选择的卡片上的数字之和能被整除的概率为( )
A. B. C. D.
6.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上一面的点数是3”为事件B,则事件A,B中至少有一个发生的概率是( )
A. B. C. D.
7.费马小定理:若是质数,且,互质,那么的次方除以所得的余数恒等于1.依此定理,若在数集中任取两个数,其中一个作为,另一个作为,则所取的两个数符合费马小定理的概率为( )
A. B. C. D.
8.不透明的口袋内装有红色 绿色和蓝色小球各2个,一次任意摸出2个小球,则与事件“2个小球都为红色”互斥而不对立的事件有( )
A.2个小球不全为红色 B.2个小球恰有一个红色
C.2个小球至少有一个红色 D.2个小球不全为绿色
二、多选题
9.不透明的口袋内装有红色 绿色和蓝色卡片各2张,一次任意取出2张卡片,则与事件“2张卡片都为红色”互斥而不对立的事件有( )
A.2张卡片都不是红色 B.2张卡片恰有一张红色
C.2张卡片至少有一张红色 D.2张卡片都为绿色
10.连掷一枚均匀的骰子两次,所得向上的点数分别为a,b,记,则下列说法错误的是( )
A.事件“”的概率为
B.事件“”的概率为
C.事件“”与“”互为对立事件
D.事件“m是奇数”与“”互为互斥事件
11.某展会安排了分别标有序号为“号”“号”“号”的三辆车,等可能的随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计了两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“号”车的概率分别为,则( )
A. B. C. D.
12.甲、乙两人下棋,甲获胜的概率为,甲不输的概率为,下列说法正确的是( )
A.和棋的概率是 B.乙不输的概率是
C.乙胜的概率是 D.甲输的概率是
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘.10天后,又从池塘内捞出60条鱼,其中有标记的有2条.根据以上数据可以估计该池塘内共有___________条鱼.
14.下列试验是古典概型的为______.
①从6名同学中选出4人参加数学竞赛,每人被选中的可能性大小;
②同时掷两枚骰子,点数和为6的概率;
③近三天中有一天降雨的概率;
④甲乙等10人站成一排,其中甲、乙相邻的概率.
15.小张,小李,小王三位同学之间相互传球,假设他们相互间传球是等可能的,并且由小张开始传球,则经过5次传球后,球仍回到小张手中的概率为________.
16.小华、小明、小李小章去A,B,C三个工厂参加社会实践,要求每个工厂都有人去,且这四人都在这三个工厂实践,则小华和小李都没去B工厂的概率是________.
四、解答题
17.某校学生营养餐由A和B两家配餐公司配送. 学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分. 根据收集的80份问卷的评分,得到A公司满意度评分的频率分布直方图和B公司满意度评分的频数分布表:
(1)如果该学校有名学生,估计该学校学生对A公司满意度评分和B公司满意度评分不低于分的分别有多少人;
(2)从满意度评分不低于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率.
18.良好的体育锻炼习惯,对学生的学习和生活都非常有益.某校为了解学生的课外体育锻炼时间情况,在全体学生中随机抽取了200名学生进行调查,并将数据分成六组,得到如图所示的频率分布直方图.将平均每天课外体育锻炼时间在上的学生评价为锻炼达标,将平均每天课外体育锻炼时间在上的学生评价为锻炼不达标.
(1)估计这200名学生每天课外体育锻炼时间的第50百分位数与平均值(同一组中的数据用该组区间的中点值为代表);
(2)在上述锻炼达标的学生中按分层抽样的方法抽取8名,再从这8名同学中随机抽取2名,求这两名同学中至少有一名每天体育锻炼时间在的概率.
19.某花店每天以每枝元的价格从农场购进若干枝玫瑰花,然后以每枝元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(1)若花店一天购进枝玫瑰花,求当天的利润(单位:元)关于当天需求量(单位:枝,)的函数解析式.
(2)花店记录了天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n 14 15 16 17 18 19 20
频数 10 20 16 16 15 13 10
(i)假设花店在这天内每天购进枝玫瑰花,求这天的日利润(单位:元)的平均数;
(ii)若花店一天购进枝玫瑰花,以天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于元的概率.
20.新高考取消文理分科,采用选科模式,这赋予了学生充分的自由选择权.新高考地区某校为了解本校高一年级将来高考选考物理的情况,随机选取了100名高一学生,将他们某次物理测试成绩(满分100分)按照,,,,分成5组,制成如图所示的频率分布直方图.
(1)求图中的值并估计这100名学生本次物理测试成绩的中位数.
(2)根据调查,本次物理测试成绩不低于60分的学生,高考将选考物理科目;成绩低于60分的学生,高考将不选考物理科目.按分层抽样的方法从测试成绩在,的学生中选取5人,再从这5人中任意选取2人,求这2人中至少有1人高考选考物理科目的概率.
21.小陈以游戏方式决定是参加学校合唱团还是参加学校足球队.游戏规则:从,,,,,(如图)这6个点中任取2个点,记选取的在轴上的点的个数为.若就参加学校合唱团,否则就参加学校足球队求小陈参加学校足球队的概率.
22.一部车床生产某种零件的不合格品率为2%,若从这部车床生产的一组5个零件的随机样本中发现有2个或2个以上的不合格品,则停机维修.试求停机维修的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
利用古典概型计算公式计算即可
【详解】
从编号分别为,,,,的五个大小完全相同的小球中,随机取出三个小球
共有种不同的取法,
恰好有两个小球编号相邻的有:
,共有6种
所以概率为
故选:C
2.D
【解析】
【分析】
利用古典概型的概率求解.
【详解】
该班同学的疫苗接种完成率为.
故选:D
3.D
【解析】
【分析】
根据事件的运算逐个判断即可.
【详解】
事件A为抽到一件正品,故A错误.
事件为抽到乙的反面,即抽到正品,故B错误.
事件为抽到丙的反面,即抽到正品,故C错误.
事件为抽取甲级产品的反面,即抽到次品,故D正确.
故选:D.
4.C
【解析】
【分析】
由独立事件概率乘法公式可求得甲和乙安装完成时间均多于丙的概率,由对立事件概率公式可求得结果.
【详解】
甲和乙安装完成时间均多于丙的概率为,
甲和乙中至少有一人安装完成时间少于丙的概率为.
故选:C.
5.A
【解析】
【分析】
利用古典概型的概率公式即求.
【详解】
由题知甲、乙两名运动员选择的卡片结果有:
共9种;
其中他们选择的卡片上的数字之和能被整除的有:共3种.
故他们选择的卡片上的数字之和能被整除的概率为.
故选:A
6.C
【解析】
【分析】
正难则反,先计算出事件A,B都不发生的概率,用1减去对应概率即可.
【详解】
由题可知,,则事件A,B都不发生的概率为,故事件A,B中至少有一个发生的概率是.
故选:C
7.A
【解析】
【分析】
利用古典概型的概率求解.
【详解】
样本点表示,,余类推,则样本空间,共有12个样本点.
记事件表示“所取的两个数符合费马小定理”,则事件所含的样本点为,,,,,,,共7个.
所以所取的两个数符合费马小定理的概率.
故选:A.
8.B
【解析】
【分析】
对于A两个事件是对立的事件,故A错误;对于B,两个事件是互斥而不对立的,故B正确;对于C,两个事件不是互斥事件,故C错误;对于D,两个事件可以同时发生,不互斥,故D也错误.
【详解】
一个口袋内装有大小、形状相同的红色、绿色和蓝色小球各2个,一次任意取出2个小球,
对于A,2个小球不全为红球与事件“2个小球都为红色”是对立的事件,故A错误;
对于B,2个小球恰有1个红球与事件“2个小球都为红色”互斥而不对立的事件,故B正确;
对于C,2个小球至少有1个红球与事件“2个小球都为红色”能同时发生,不是互斥事件,故C错误;
对于D,2个小球不全为绿球与事件“2个小球都为红色”是可以同时发生的事件,不是互斥事件,故D错误.
故选:B.
9.ABD
【解析】
【分析】
列举出所有情况,然后再利用互斥事件和对立事件的定义判断.
【详解】
解:6张卡片中一次取出张卡片的所有情况有:
“2张都为红色” “2张都为绿色” “2张都为蓝色” “1张为红色1张为绿色” “1张为红色1张为蓝色” “1张为绿色1张为蓝色”,
选项中给出的四个事件中与“2张都为红色”互斥而非对立的事件是:“2张都不是红色”,“2张恰有一张红色”,“2张都为绿色”,
其中“2张至少一张为红色”包含事件“2张都为红色”,二者并非互斥.
故选:ABD.
10.ABC
【解析】
【分析】
利用列举法和概率公式计算可知,AB错误,根据互斥、对立事件的概念可知,C错误,D正确.
【详解】
连掷一枚均匀的骰子两次,所得向上的点数有:,,,,,,共36种,
事件“”所包含的基本事件有:共1个,所以事件“”的概率为,故A错误;事件“” 所包含的基本事件有:,共1个,所以事件“”的概率为,故B错误;
事件“”与“”可以同时发生,不是对立事件,故C错误;
事件“m是奇数”与“”不能同时发生,所以事件“m是奇数”与“”互为互斥事件,故D正确.
故选:ABC
11.ACD
【解析】
【分析】
利用列举法求出方案一坐到“3号”车的概率,利用古典摡型求出方案二坐到“3号”车的概率,即可得到答案.
【详解】
由题意,分别标有序号为“1号”“2号”“3号”的三辆车,等坑随机顺序前往酒店接嘉宾,
基本事件有:,共6种,
设计两种方案:方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车,
则方案一坐到“3号”车包含的基本事件有:,共有3种,
所以方案一的概率为;
方案二:直接乘坐第一辆车,则方案二坐到“号”车的概率为,
所以.
故选:ACD .
12.ABD
【解析】
【分析】
利用互斥事件、对立事件的概率公式计算出各选项中事件的概率,由此可判断各选项的正误.
【详解】
对于A选项,和棋的概率是,A对;
对于B选项,乙不输的概率是,B对;
对于C选项,乙胜的概率是,C错;
对于D选项,甲输的概率是,D对.
故选:ABD.
13.900
【解析】
【分析】
估计该池塘内共有n条鱼,利用等可能事件概率计算公式列方程,能求出n的值.
【详解】
解:估计该池塘内共有n条鱼,
则,
解得n=900.
故答案为:900.
14.①②④
【解析】
【分析】
根据古典概型的特点,结合每个选项进行逐一分析,即可判断和选择.
【详解】
因为古典概型需要满足基本事件是有限个,且每个基本事件的概率相等,
据此①②④均符合要求,③不满足等可能的要求,因为降雨受多方面因素影响.
故答案为:①②④.
15.##0.3125
【解析】
【分析】
画出树状图列出基本事件再计算概率即可.
【详解】
根据题意,列出树状图如下:
由树状图可知,5次传球后的基本事件总数为32,球回到小张手中的基本事件数为10.
所以5次传球后球仍回到小张手中的概率为.
故答案为:.
16.
【解析】
【分析】
求出总的分配方法数,再按去1人或2人分类求得小华和小李都没去B工厂的方法数,然后由概率公式计算.
【详解】
由题意可知总的分配情况有种,其中满足条件的情况有种,故所求概率.
故答案为:.
17.(1)对A公司满意度评分不低于分的有人,对B公司满意度评分不低于分的有人;
(2).
【解析】
【分析】
(1)利用频率分布直方图可知A公司满意度评分不低于80分的频率,利用B公司满意度评分的频数分布表可知40人中不低于80分的频数,即求;
(2)利用列举法解决古典概型概率问题.
(1)
由A公司满意度评分的频率分布直方图可知不低于80分的频率为,
所以估计该校学生对A公司满意度评分不低于分的有人;
由B公司满意度评分的频数分布表可知40人中不低于80分的频数为,
频率为,
所以估计该校学生对B公司满意度评分不低于分的有人.
(2)
满意度不低于90分的问卷共有6份,其中4份评价公司,设为,2份评价B公司,设为,
从这6份问卷中随机取2份,样本空间,,,,,,,,,,,,,,}共有15种,
设两份问卷均是评价A公司为事件C,则C={,,,,,}共有6种,
则有,
所以这两份问卷都是给A公司评分的概率为.
18.(1)28.125,28.7;
(2)﹒
【解析】
【分析】
(1)根据已知条件,结合百分位数和平均值公式,即可求解;
(2)根据题意,求出从这8名同学中随机抽取2名的抽取方法数量m,求出这两名同学中没有一名每天体育锻炼时间在的抽取方法n,则所求概率为.
(1)
∵前2组频率为0.08+0.16=0.24,前三组的频率为0.24+0.32=0.56,∴第50百分位数在第3组,设第50百分位数为m,则,解得,
平均数为;
(2)
根据题意可得,从这8名同学中随机抽取2名,共有种不同的抽取方法,
抽取的8名同学中,每天体育锻炼时间在的有6名,每天体育锻炼时间在的有2名,这两名同学中没有一名每天体育锻炼时间在的抽取方法有种,∴这两名同学中至少有一名每天体育锻炼时间在的抽取方法有种,故所求概率为
19.(1);
(2)(i);(ii)
【解析】
【分析】
(1)根据卖出一枝可得利润5元,卖不出一枝赔本5元,即可建立分段函数;
(2)根据题意求得天所有的利润,除以即得每日利润;
(3)根据(2)中所求每日利润,结合利润不少于元的要求,将对应频率相加即可.
(1)
当需求量时,每日利润元;
当需求量时,每日利润元;
故每日利润关于的函数为:
(2)
(i)根据题意,天内,
有天的利润为元,有天的利润为元,
有天的利润为元,有天的利润为元,
故这天内,日利润的平均值为:元.
(ii)显然要满足题意,只需每日需求量即可.
故当天的利润不少于元的概率为:.
20.(1),中位数为;
(2).
【解析】
【分析】
(1)由频率和为1求参数a,根据直方图及中位数的性质求中位数即可.
(2)首先由分层抽样原则求选取的5人在、的人数分布情况,再应用列举法求古典概型的概率即可.
(1)
由图知:,解得.
学生成绩在的频率为;
学生成绩在的频率为.
设这100名学生本次物理测试成绩的中位数为,则,解得,
故估计这100名学生本次物理测试成绩的中位数为.
(2)
由(1)知,学生成绩在的频数为,学生成绩在的频数为.
按分层抽样的方法从中选取5人,则成绩在的学生被抽取人,分别记为,,成绩在的学生被抽取人,分别记为,,.
从中任意选取2人,有,,,,,,,,,这10种选法,
其中至少有1人高考选考物理科目的选法有,,,,,,,,这9种,
∴这2人中至少有1人高考选考物理科目的概率.
21.
【解析】
【分析】
根据古典概型公式,结合列举法、对立事件的概率公式进行求解即可.
【详解】
从,,,,,中任取2个点包含的所有情况为,,,,,,,,,,,,,,,共有15种,当时,所取的2个点均不在轴上,即从,,,中任取2个点,所有可能的情况为,,,,,,共6种,
所以小陈参加学校合唱团的概率为,
所以小陈参加学校足球队的概率.
22.0.004.
【解析】
【分析】
利用对立事件概率计算公式和次独立重复试验中事件恰好发生次的概率计算公式直接求解.
【详解】
一部车床生产某种零件的不合格品率为,合格的概率为,
事件:5个零件的随机样本中发现有2个或2个以上的不合格品,
事件:5个零件的随机样本中都合格或只有一个不合格,
根据独立重复事件的概率公式:
根据对立事件的概率公式:,
综上所述,结论是:停机维修的概率约为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
