直线与圆的位置关系

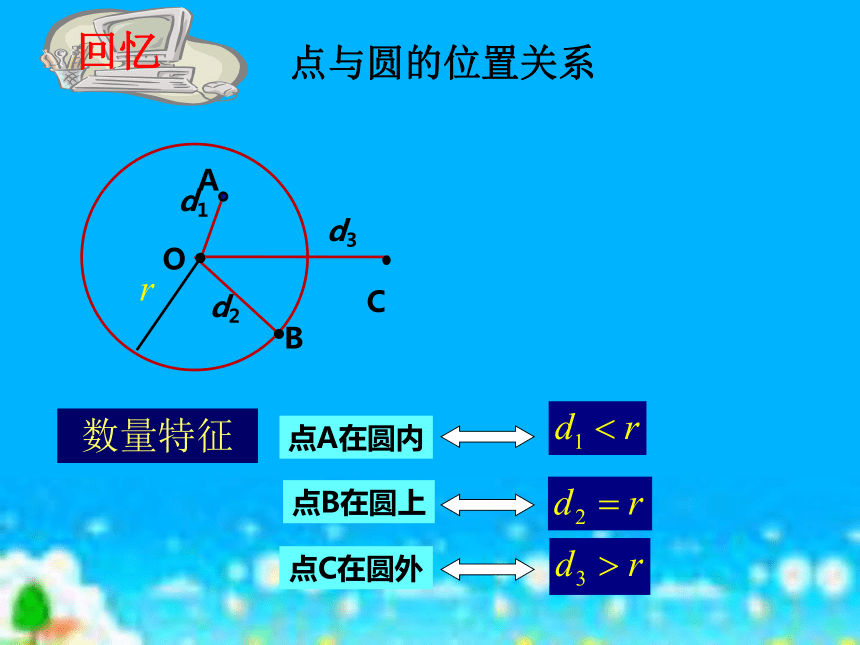
课件18张PPT。直线与圆的位置关系第24章点与圆的位置关系点B在圆上点A在圆内点C在圆外数量特征直线和圆的位置有
何关系？？？.Ol特点：.O叫做直线和圆相离。直线和圆没有公共点，l特点：直线和圆有唯一的公共点，叫做直线和圆相切。这时的直线叫切线，
唯一的公共点叫切点。.Ol特点：直线和圆有两个公共点，叫直线和圆相交，这时的直线叫做圆的割线。一、直线与圆的位置关系
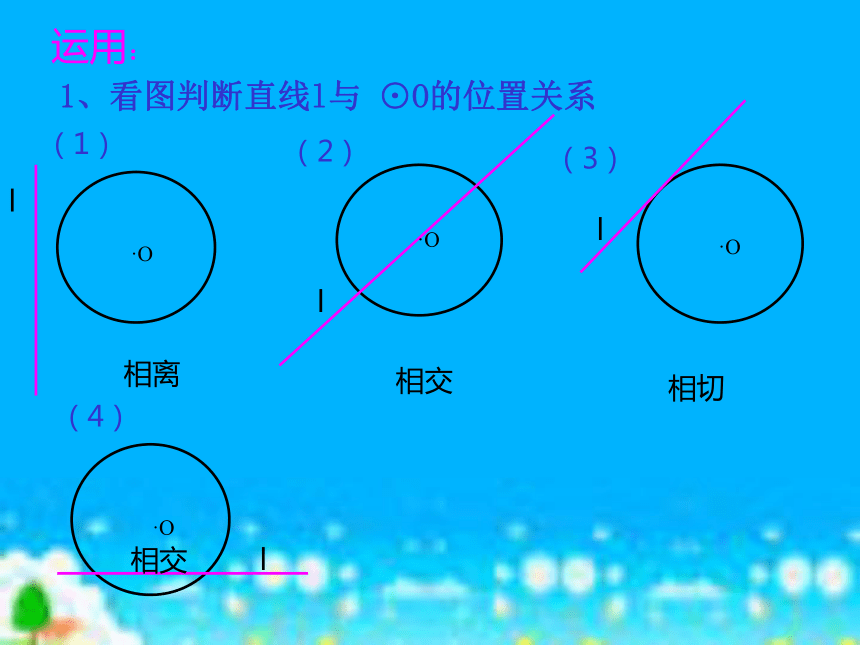
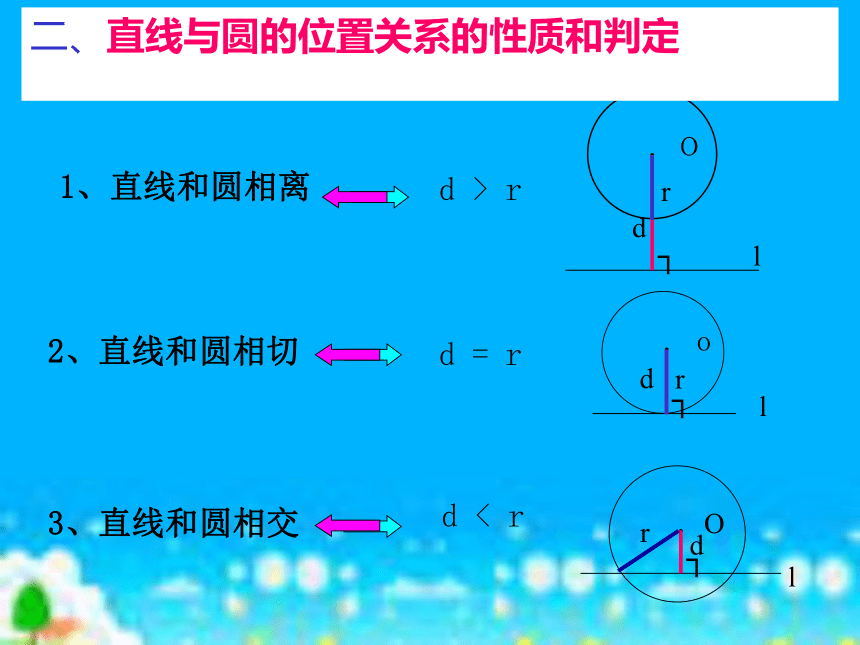
（用公共点的个数来区分）.A.A.B切点运用：1、看图判断直线l与 ⊙O的位置关系（1）（2）（3）（4）相离相切相交相交llll·O·O·O·O2、直线和圆相切d = r3、直线和圆相交d < rd二、直线和圆的位置关系（设圆心o到直线l的距离为d，圆的半径为r）1、直线和圆相离d > r二、直线与圆的位置关系的性质和判定
练习1 １、直线与圆最多有两个公共点 。… （　） √×？3 、若A是⊙O上一点， 则直线AB与⊙O相切 。( ).A.O２、若直线与圆相交，则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点，则过点C的直线CD与
⊙O 相交或相离。………（ ）××.C相交相切相离d > 5cmd = 5cmd < 5cm练习20cm≤210思考：圆心A到X轴、
Y轴的距离各是多少?例题1：O 已知⊙A的直径为6，点A的坐标为（-3，-4），则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切例题2：在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆
与直线AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm (3)r=3cm。BCAD453？例: Rt△ABC,∠C=90°AC=3cm，BC=4cm，以C为圆心，r为半径的圆与直线AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm
(3)r=3cm。即圆心C到AB的距离d=2.4cm。（1）当r=2cm时， ∵d＞r，
∴⊙C与AB相离。（2）当r=2.4cm时，∵d=r，
∴⊙C与AB相切。（3）当r=3cm时， ∵d＜r，
∴⊙C与AB相交。ABCAD453d=2.4 4、当 r 满足 ________ 时,
⊙C与线段AB只有一个公共点.在Rt△ABC中，∠C=90°，
AC=3cm，BC=4cm，
以C为圆心，r为半径作圆。想一想? 当r满足___________
_____________ 时,⊙C与线段AB只有一个公共点. r=2.4cmBCAD453d=2.4cm 或3cm 1、如图，已知∠AOB=30°，M为OB上一点，且OM=5cm，以M为圆心、以r为半径的圆与直线OA有怎样的位置关系？为什么 ？ ⑴　r =2cm； ⑵ r =4cm； ⑶ r =2.5cm。 解：过点M作MC⊥OA于C ，
∵ ∠AOB=30°， OM=5cm， ∴ MC=2.5cm ⑴ ∵ d=MC=2.5， r=2 即d ＞r
∴ ⊙O与OA相离；
⑵ ∵ d=MC=2.5， r=4 即d ＜ r
∴ ⊙O与OA相交；
⑶ ∵ d=MC=2.5， r=2.5 即d= r
∴ ⊙O与OA相切.课堂练习.小结：0d>r1d=r切点切线2d
1.直线与圆的位置关系三种：相离、相切和相交．小 结 （2）另一种是根据圆心到直线的距离d与圆半径r的大小
关系来进行识别：
（1）一种是根据定义进行识别： 随堂检测
1．⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l　
　与⊙O没有公共点，则d为（　）：
　A．d ＞3 B．d<3 C．d ≤3 D．d =3
2．直线l上的一点到圆心O的距离等于⊙O的半径，则直线l与⊙O（ ）
A、相离；B、相切；C、相交；D、相切或相交。
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AD√相离 1．若⊙O与直线m的距离为d，⊙O 的半径为r，若d，r
是方程的两个根，则直线m与⊙O的位置的两个根，且直线m2、若d，r是方程与⊙O的位置关系是相切，则a的值是 。关系是 。思考题： 3、如图：菱形ABCD的边长为5cm，∠B=60°当以A为圆心的圆与BC相切时，半径是 ，此时⊙A与CD的位置关系是 。