华师大版数学七年级下册7.2二元一次方程的组解法(3)课件(共24张PPT)
文档属性
| 名称 | 华师大版数学七年级下册7.2二元一次方程的组解法(3)课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 15:02:29 | ||
图片预览








文档简介
(共24张PPT)
2022年春华师大版数学
七年级下册数学精品课件
二元一次方程组解法(三)
学习目标
会根据方程组特点灵活应用加减法解方程组.
熟练运用加减消元法解二元一次方程组.
1.什么是加减消元法?
2.什么情况下可以用加减消元法?
当二元一次方程组中的两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
当方程组中同一未知数的系数相同或相反时,把两个方程相减或相加,消去其中的一个
未知数,得到一个一元一次方程.这种解法体现了转化的数学思想.
复习回顾
3.用已学过的知识解下列方程
4.利用学过的方法解方程,看谁解的快?
解:
复习回顾
①
②
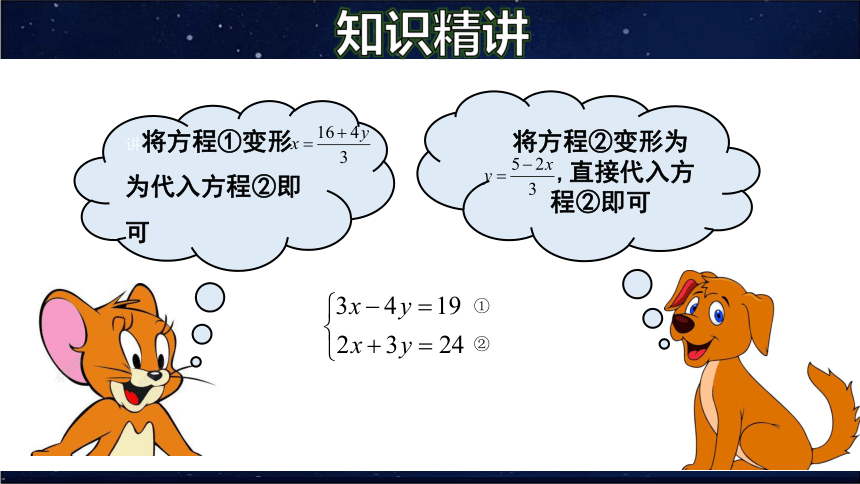
讲将方程①变形
为代入方程②即可
将方程②变形为
,直接代入方程②即可
②
①
知识精讲
方程①②的每一个未知数的系数即不相同也不相反,该怎么办?
......
既然未知数的系数不同,可不可以将他们化成系数相同呢?
②
①
知识精讲
方程组就变成了
如果给方程①乘以
2,方程②乘以3
②
①
方程组就变成了
②
①
知识精讲
根据 思路,解方程
②
①
解:①×2、②×3得
④
③
③-④得
将y=2代入方程①,得
所以
知识精讲
例1.解方程
②
①
解:①×5,②×3
④
③
③-④得
将y=2代入方程①得
所以
典例解析
能否变形后消去y呢?
同一未知数的系数 时,利用等式的性质,使
得未知数的系数 .
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
总结提升
解二元一次方程组加减法的一般步骤
1.对齐:含有相同未知数的项和常数项对齐;
2.变系数:将两个方程的同一个未知数的系数变相等或互为相反数;
3.相加减:系数相等,方程相减;系数相反,方程相加。化为一元一次方程;
4.求解:解这个一元一次方程;
5.回代:求出的解代回原方程组中的方程,求出另一个未知数的值;
6.写解:写出方程组的解.
总结提升
1.用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2
把y=2代入①,
解得: x=3
②×2得:
6x+9y=36 ③
6x+8y=34 ④
针对练习
解: ②×4得:
所以原方程组的解为
①
2.解方程组:
②
③
①+③得:7x = 35,
解得:x = 5.
把x = 5代入②得,y = 1.
4x-4y=16
针对练习
①
②
例2.解方程组
解:由① + ②,得 4(x+y)=36
所以 x+y=9 ③
由① - ②,得 6(x-y)=24
所以 x-y=4 ④
解由③④组成的方程组
解得
法二:
整理得
【点睛】整体代入法(换元法)是数学中的重要方法之一,这种方法往
往能使运算更简便.
典例解析
1.用加减法解方程 时,( )(多选)
A 方程①×4,②×3,再相加
B 方程①×4,②×3,再相减
C 方程①×2,②×5,再相加
D 方程①×4,②×3,再相加
①
②
AC
达标检测
2.若 是二元一次方程,则a= ,b= .
3.已知 ,则x= ,y= .
7
8
2
1
达标检测
4.解下列方程:
解:
达标检测
解:由①×6,②×4,得
由③-④得: y= -1
所以原方程组的解是
把y =-1代入② ,解得:
①
②
5.解方程
④
③
达标检测
同一未知数的系数 时,利用等式的性质,使
得未知数的系数 .
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
小结梳理
解二元一次方程组加减法的一般步骤
1.对齐:含有相同未知数的项和常数项对齐;
2.变系数:将两个方程的同一个未知数的系数变相等或互为相反数;
3.相加减:系数相等,方程相减;系数相反,方程相加。化为一元一次方程;
4.求解:解这个一元一次方程;
5.回代:求出的解代回原方程组中的方程,求出另一个未知数的值;
6.写解:写出方程组的解.
小结梳理
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
二元一次方程组解法(三)
学习目标
会根据方程组特点灵活应用加减法解方程组.
熟练运用加减消元法解二元一次方程组.
1.什么是加减消元法?
2.什么情况下可以用加减消元法?
当二元一次方程组中的两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
当方程组中同一未知数的系数相同或相反时,把两个方程相减或相加,消去其中的一个
未知数,得到一个一元一次方程.这种解法体现了转化的数学思想.
复习回顾
3.用已学过的知识解下列方程
4.利用学过的方法解方程,看谁解的快?
解:
复习回顾
①
②
讲将方程①变形
为代入方程②即可
将方程②变形为
,直接代入方程②即可
②
①
知识精讲
方程①②的每一个未知数的系数即不相同也不相反,该怎么办?
......
既然未知数的系数不同,可不可以将他们化成系数相同呢?
②
①
知识精讲
方程组就变成了
如果给方程①乘以
2,方程②乘以3
②
①
方程组就变成了
②
①
知识精讲
根据 思路,解方程
②
①
解:①×2、②×3得
④
③
③-④得
将y=2代入方程①,得
所以
知识精讲
例1.解方程
②
①
解:①×5,②×3
④
③
③-④得
将y=2代入方程①得
所以
典例解析
能否变形后消去y呢?
同一未知数的系数 时,利用等式的性质,使
得未知数的系数 .
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
总结提升
解二元一次方程组加减法的一般步骤
1.对齐:含有相同未知数的项和常数项对齐;
2.变系数:将两个方程的同一个未知数的系数变相等或互为相反数;
3.相加减:系数相等,方程相减;系数相反,方程相加。化为一元一次方程;
4.求解:解这个一元一次方程;
5.回代:求出的解代回原方程组中的方程,求出另一个未知数的值;
6.写解:写出方程组的解.
总结提升
1.用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2
把y=2代入①,
解得: x=3
②×2得:
6x+9y=36 ③
6x+8y=34 ④
针对练习
解: ②×4得:
所以原方程组的解为
①
2.解方程组:
②
③
①+③得:7x = 35,
解得:x = 5.
把x = 5代入②得,y = 1.
4x-4y=16
针对练习
①
②
例2.解方程组
解:由① + ②,得 4(x+y)=36
所以 x+y=9 ③
由① - ②,得 6(x-y)=24
所以 x-y=4 ④
解由③④组成的方程组
解得
法二:
整理得
【点睛】整体代入法(换元法)是数学中的重要方法之一,这种方法往
往能使运算更简便.
典例解析
1.用加减法解方程 时,( )(多选)
A 方程①×4,②×3,再相加
B 方程①×4,②×3,再相减
C 方程①×2,②×5,再相加
D 方程①×4,②×3,再相加
①
②
AC
达标检测
2.若 是二元一次方程,则a= ,b= .
3.已知 ,则x= ,y= .
7
8
2
1
达标检测
4.解下列方程:
解:
达标检测
解:由①×6,②×4,得
由③-④得: y= -1
所以原方程组的解是
把y =-1代入② ,解得:
①
②
5.解方程
④
③
达标检测
同一未知数的系数 时,利用等式的性质,使
得未知数的系数 .
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
小结梳理
解二元一次方程组加减法的一般步骤
1.对齐:含有相同未知数的项和常数项对齐;
2.变系数:将两个方程的同一个未知数的系数变相等或互为相反数;
3.相加减:系数相等,方程相减;系数相反,方程相加。化为一元一次方程;
4.求解:解这个一元一次方程;
5.回代:求出的解代回原方程组中的方程,求出另一个未知数的值;
6.写解:写出方程组的解.
小结梳理
https://www.21cnjy.com/help/help_extract.php
