华师大版数学八年级下册16.4.2 科学记数法 课件(共22张PPT)
文档属性
| 名称 | 华师大版数学八年级下册16.4.2 科学记数法 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 14:57:05 | ||
图片预览








文档简介
2022年春华师大版数学
八年级下册数学精品课件
16.4.2 科学记数法
学习目标
会用科学记数法表示绝对值小于1的数.
能灵活运用科学记数法解决实际问题.
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤????<10,n是正整数.
?
例如,1.864000可以写成 .
怎样把0.0000864用科学记数法表示?
8.64×105
想一想:
复习回顾
B
2.用科学记数法表示2130000,正确的是( )
(A)21.3×105
(B)2.13×106
(C)0.213×107
(D)213×104
1.计算机的存储器完成一次存储的时间一般以百万分之一秒或十亿分之一秒为单位.
我们的周围还有很多很小的数
知识精讲
2.存在于生物体内的某种细胞的直径约为百万分之一米,即1微米.
3.人的头发丝的直径大约为0.000 07米,这个数已经很小了,但还有更小的如纳米,1纳米 = 十亿分之一米 .
观察:
指数与运算结果中0的个数有什么关系?
10的-n次幂,在1前面有______个0.
计算:
0.1
0.01
0.001
0.0001
0.00001
你发现了什么规律?
n
例如:
0.00001=_______; 0.0000001=_______.
知识精讲
所以, 0.0000864=8.64 ×0.00001=8.64 ×10-5.
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整数,1≤∣a∣<10.
知识精讲
绝对值较大的数表示成 的形式
绝对值较小的数表示成 的形式
科学记数法
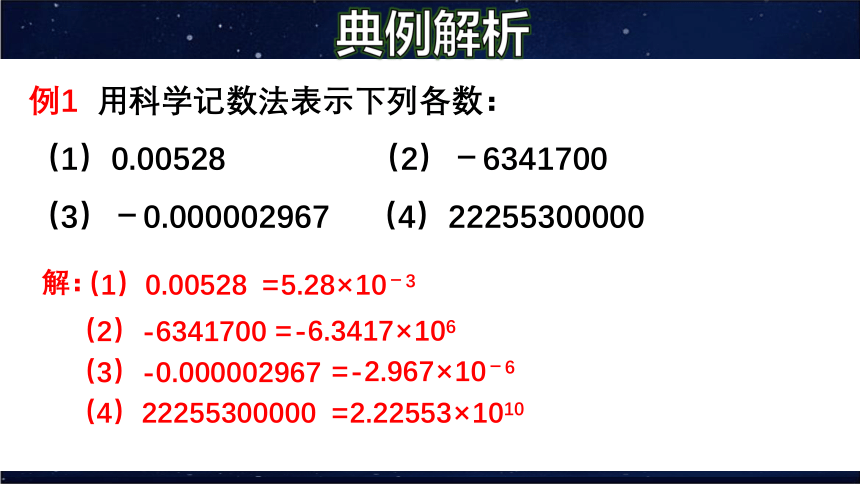
例1 用科学记数法表示下列各数:
(1)0.00528 (2)-6341700
(3)-0.000002967 (4)22255300000
=5.28×10-3
解:
(1)0.00528
=-6.3417×106
(2)-6341700
(4)22255300000
(3)-0.000002967
=-2.967×10-6
=2.22553×1010
典例解析
用科学记数法表示一些绝对值小于1的数的方法:
即利用10的负整数次幂,把一个绝对值小于1的数表示成a×10-n的形式,其中n是正整数,1 ≤ ????<10. n等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面这个零).
?
总结提升
=7.2×0.00001
=7.2×10-5
=1.5×10-9
0.000072
0.0000000015
=1.5×0.000000001
针对练习
用科学记数法表示下列各数:
例2 用小数表示下列各数:
解:
0.00023
0.000000491
-0.0000000568
典例解析
用小数表示下列各数:
(1)2×10-7; (2)3.14×10-5; (3)7.08×10-3; (4)2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708;
(4)2.17×10-1=0.217.
针对练习
例3 1.比较大小:
(1)3.01×10-4_______ 9.5×10-3
<
(2)3.01×10-4______3.10×10-4
2.计算:(结果用科学记数法表示)
(6×10-3)×(1.8×10-4)
<
解:
原式=
(6×1.8)
×
(10-3×10-4)
=
10.8
×
10-7
=
1.08×10-6
10-7
=
1.08×10
×
典例解析
例4 一个纳米粒子的直径是35纳米,它等于多少米?请用科学记数法表示.
(1纳米=10-9米)
∴35纳米=35×10-9米
而35×10-9= ×10-9
=3.5×101+(-9)
所以这个纳米粒子的直径为3.5×10-8米.
∵1纳米=10-9米
解:
=3.5×10-8
(3.5×10)
典例解析
纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
针对练习
1.用科学记数法表示:
(1)0.000 03; (2)-0.000 006 4;
(3)0.000 0314;
2.用科学记数法填空:
(1)1 s是1 μs的1 000 000倍,则1 μs=______s;
(2)1 mg=______kg;(3)1 μm =______m;
(4)1 nm=______ μm ;(5)1 cm2=______ m2 ;
(6)1 ml =______m3.
达标检测
4.下列是用科学记数法表示的数,写出原来的数.
(1)2×10-8 (2)7.001×10-6
3.计算:
(1)(2×10-6)× (3.2×103)
(2)(2×10-6)2 ÷ (10-4)3.
答案:(1)0.000 000 02 (2)0.000 007 001
= 6.4×10-3;
= 4
达标检测
5.比较大小:
(1)3.01×10-4_______9.5×10-3
(2)3.01×10-4________3.10×10-4
<
<
6.用科学记数法把0.000 009 405表示成
9.405×10n,那么n= .
-6
达标检测
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整数,1≤∣a∣<10.
小结梳理
绝对值较大的数表示成 的形式
绝对值较小的数表示成 的形式
科学记数法
https://www.21cnjy.com/help/help_extract.php
八年级下册数学精品课件
16.4.2 科学记数法
学习目标
会用科学记数法表示绝对值小于1的数.
能灵活运用科学记数法解决实际问题.
科学记数法:绝对值大于10的数记成a×10n的形式,其中1≤????<10,n是正整数.
?
例如,1.864000可以写成 .
怎样把0.0000864用科学记数法表示?
8.64×105
想一想:
复习回顾
B
2.用科学记数法表示2130000,正确的是( )
(A)21.3×105
(B)2.13×106
(C)0.213×107
(D)213×104
1.计算机的存储器完成一次存储的时间一般以百万分之一秒或十亿分之一秒为单位.
我们的周围还有很多很小的数
知识精讲
2.存在于生物体内的某种细胞的直径约为百万分之一米,即1微米.
3.人的头发丝的直径大约为0.000 07米,这个数已经很小了,但还有更小的如纳米,1纳米 = 十亿分之一米 .
观察:
指数与运算结果中0的个数有什么关系?
10的-n次幂,在1前面有______个0.
计算:
0.1
0.01
0.001
0.0001
0.00001
你发现了什么规律?
n
例如:
0.00001=_______; 0.0000001=_______.
知识精讲
所以, 0.0000864=8.64 ×0.00001=8.64 ×10-5.
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整数,1≤∣a∣<10.
知识精讲
绝对值较大的数表示成 的形式
绝对值较小的数表示成 的形式
科学记数法
例1 用科学记数法表示下列各数:
(1)0.00528 (2)-6341700
(3)-0.000002967 (4)22255300000
=5.28×10-3
解:
(1)0.00528
=-6.3417×106
(2)-6341700
(4)22255300000
(3)-0.000002967
=-2.967×10-6
=2.22553×1010
典例解析
用科学记数法表示一些绝对值小于1的数的方法:
即利用10的负整数次幂,把一个绝对值小于1的数表示成a×10-n的形式,其中n是正整数,1 ≤ ????<10. n等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面这个零).
?
总结提升
=7.2×0.00001
=7.2×10-5
=1.5×10-9
0.000072
0.0000000015
=1.5×0.000000001
针对练习
用科学记数法表示下列各数:
例2 用小数表示下列各数:
解:
0.00023
0.000000491
-0.0000000568
典例解析
用小数表示下列各数:
(1)2×10-7; (2)3.14×10-5; (3)7.08×10-3; (4)2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708;
(4)2.17×10-1=0.217.
针对练习
例3 1.比较大小:
(1)3.01×10-4_______ 9.5×10-3
<
(2)3.01×10-4______3.10×10-4
2.计算:(结果用科学记数法表示)
(6×10-3)×(1.8×10-4)
<
解:
原式=
(6×1.8)
×
(10-3×10-4)
=
10.8
×
10-7
=
1.08×10-6
10-7
=
1.08×10
×
典例解析
例4 一个纳米粒子的直径是35纳米,它等于多少米?请用科学记数法表示.
(1纳米=10-9米)
∴35纳米=35×10-9米
而35×10-9= ×10-9
=3.5×101+(-9)
所以这个纳米粒子的直径为3.5×10-8米.
∵1纳米=10-9米
解:
=3.5×10-8
(3.5×10)
典例解析
纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
针对练习
1.用科学记数法表示:
(1)0.000 03; (2)-0.000 006 4;
(3)0.000 0314;
2.用科学记数法填空:
(1)1 s是1 μs的1 000 000倍,则1 μs=______s;
(2)1 mg=______kg;(3)1 μm =______m;
(4)1 nm=______ μm ;(5)1 cm2=______ m2 ;
(6)1 ml =______m3.
达标检测
4.下列是用科学记数法表示的数,写出原来的数.
(1)2×10-8 (2)7.001×10-6
3.计算:
(1)(2×10-6)× (3.2×103)
(2)(2×10-6)2 ÷ (10-4)3.
答案:(1)0.000 000 02 (2)0.000 007 001
= 6.4×10-3;
= 4
达标检测
5.比较大小:
(1)3.01×10-4_______9.5×10-3
(2)3.01×10-4________3.10×10-4
<
<
6.用科学记数法把0.000 009 405表示成
9.405×10n,那么n= .
-6
达标检测
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成a×10- n的形式,其中n是正整数,1≤∣a∣<10.
小结梳理
绝对值较大的数表示成 的形式
绝对值较小的数表示成 的形式
科学记数法
https://www.21cnjy.com/help/help_extract.php
