28.1.1 正弦同步练习(含答案)
图片预览



文档简介
28.1 锐角三角函数
第1课时 正 弦
一、选择题
1.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sin B的值为( )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,sinA=,AC=4,则AB的长为( )
A.2 B.4 C.6 D.8
3.【2021·桂林】如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
第3题图 第5题图 第6题图 第7题图
4.在Rt△ABC中,如果各边长度都扩大2倍,那么锐角A的正弦值( )
A.没有变化 B.扩大2倍 C.缩小2倍 D.不能确定
5.如图,在2×2的正方形网格中,以格点为顶点的△ABC的面积等于,则sin∠CAB的值为( )
A. B. C. D.
6.【2020·聊城】如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列各组线段的比不能表示sin∠BCD的是( )
A. B. C. D.
8.【2021·云南】在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )
A. B. C.60 D.80
9.在Rt△ABC中,∠C=90°,sin A=,BC=20,则△ABC的面积为( )
A.80 B.100 C.120 D.150
10.【2020·扬州】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为( )
A. B. C. D.
第10题图 第11题图 第12题图
11.【攀枝花中考】如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
12.如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,,则sinA的值为( )
A. B. C. D.
二、填空题
13.(1)如图,在Rt△ABC中,∠C=90°,我们把锐角A的________与________的比叫做∠A的正弦,记作________,即sin A==_______
(2)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则sinA=________,a=________,c=________,b2=__________.
第13(1)题图 第16题图 第17题图 第18题图
14.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是____.
15.在Rt△ABC中,∠C=90°,AB=3BC,则sin B= .
16.已知AE,CF是锐角三角形ABC的两条高.若AE∶CF=3∶2,则sin∠BAC∶sin∠ACB= .
17.如图,☉O是△ABC的外接圆,AD是☉O的直径,若☉O的半径是4,sinB=,则线段AC的长为 .
归纳总结
利用等角转换法求锐角三角函数值
利用等角转换法,把要求的角转化为与其相等的角,找相等角的方法有多种,可以借助平行线、等腰三角形、三角形全等(相似)和圆等知识来解决,要根据题目的条件灵活选用方法.
18.如图,在△ABC中,∠C=90°,∠A=∠CBD.若sin A=,AB=5,则CD= .
三、解答题
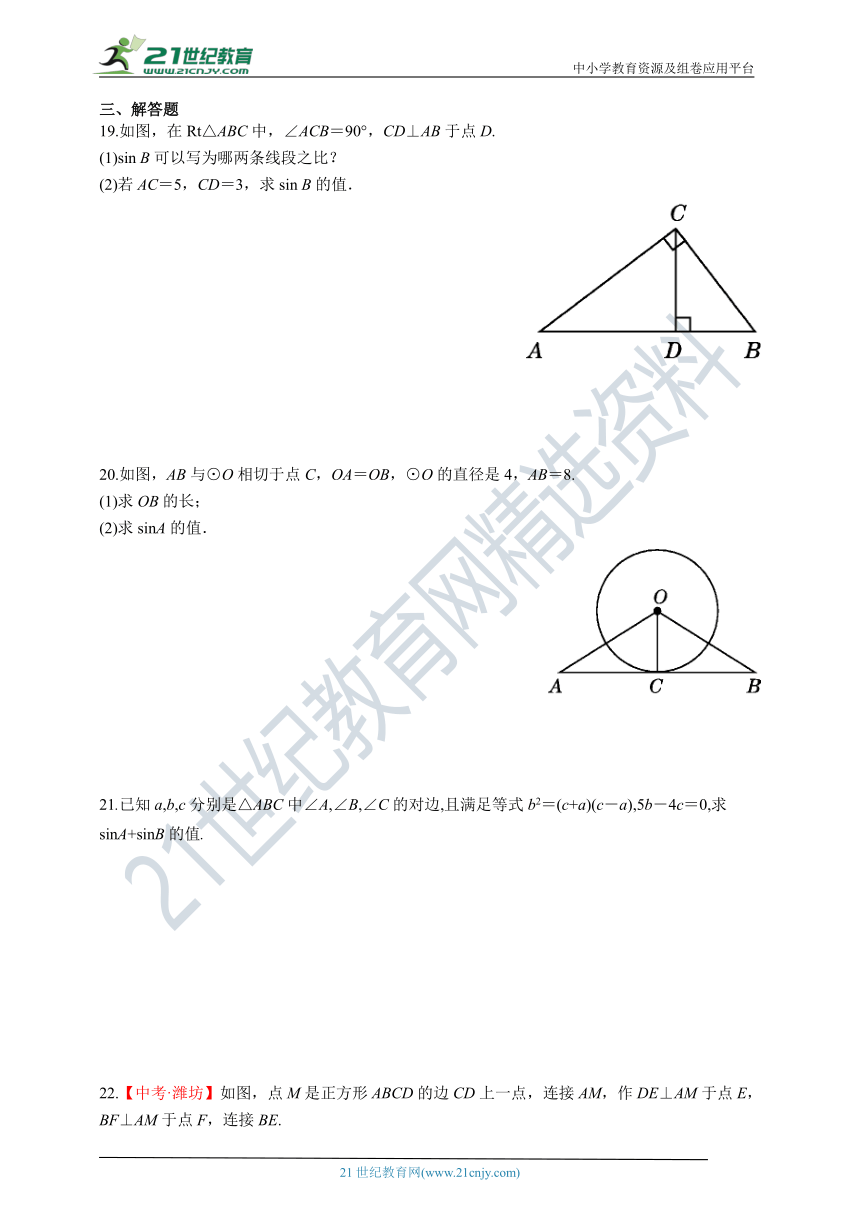
19.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)sin B可以写为哪两条线段之比?
(2)若AC=5,CD=3,求sin B的值.
20.如图,AB与⊙O相切于点C,OA=OB,⊙O的直径是4,AB=8.
(1)求OB的长;
(2)求sinA的值.
21.已知a,b,c分别是△ABC中∠A,∠B,∠C的对边,且满足等式b2=(c+a)(c-a),5b-4c=0,求sinA+sinB的值.
22.【中考·潍坊】如图,点M是正方形ABCD的边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
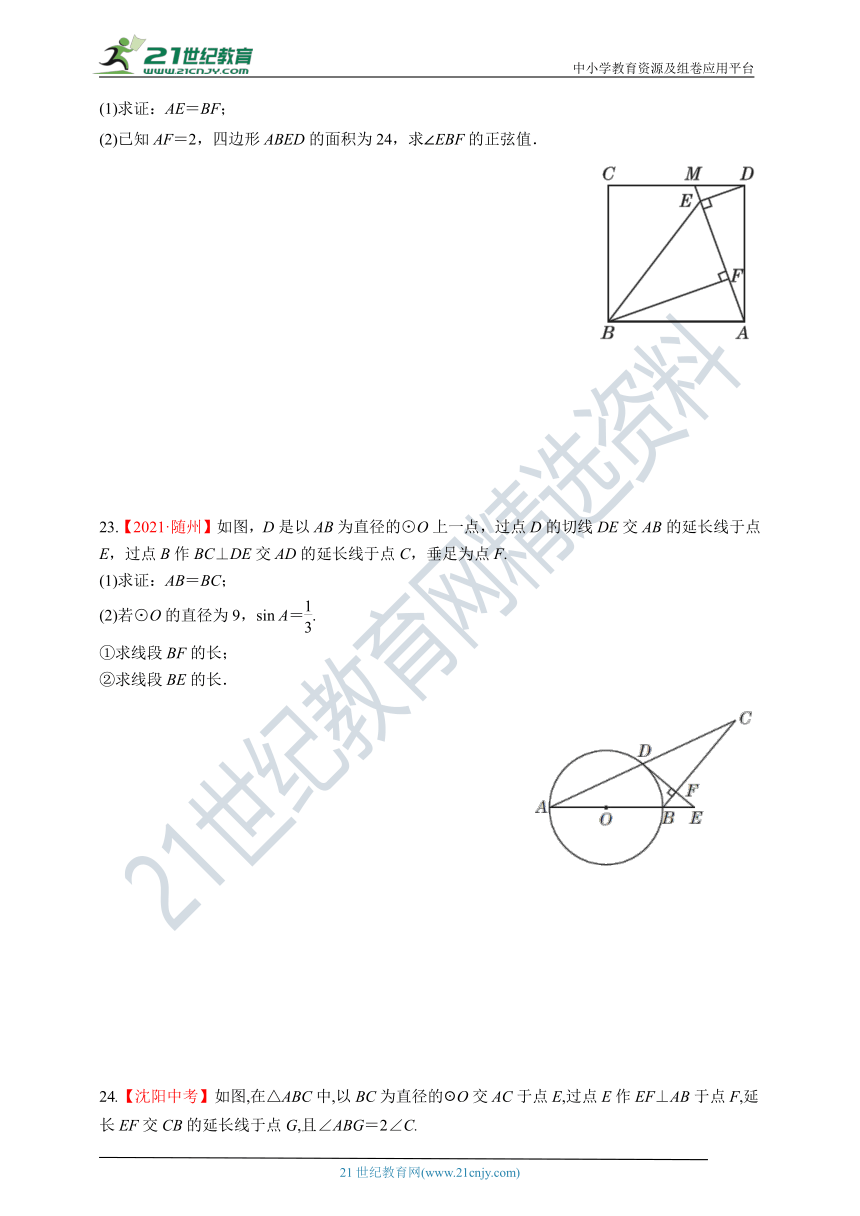
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
23.【2021·随州】如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
(2)若⊙O的直径为9,sin A=.
①求线段BF的长;
②求线段BE的长.
24.【沈阳中考】如图,在△ABC中,以BC为直径的☉O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EF是☉O的切线;
(2)若sin∠EGC=,☉O的半径是3,求AF的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sin B的值为( D )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,sinA=,AC=4,则AB的长为( C )
A.2 B.4 C.6 D.8
3.【2021·桂林】如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
【答案】D
【解析】如图,过点P作PM⊥x轴于点M,∵P(3,4),∴OM=3,PM=4,∴OP==5,∴sin α==.
第3题图 第5题图 第6题图 第7题图
4.在Rt△ABC中,如果各边长度都扩大2倍,那么锐角A的正弦值( )
A.没有变化 B.扩大2倍 C.缩小2倍 D.不能确定
【答案】A
【解析】若Rt△ABC的各边长度都扩大2倍,则所得新三角形与原三角形相似,故锐角A大小不变,其正弦值也没有变化.
5.如图,在2×2的正方形网格中,以格点为顶点的△ABC的面积等于,则sin ∠CAB的值为( B )
A. B. C. D.
6.【2020·聊城】如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( D )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列各组线段的比不能表示sin∠BCD的是( )
A. B. C. D.
【答案】C
【解析】∵CD⊥AB,∴∠CDA=90°,∴∠A+∠ACD=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°,
∴∠BCD=∠A.∵sin∠BCD=,sin A==,∴A项、B项、D项都能表示sin∠BCD.
8.【2021·云南】在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )
A. B. C.60 D.80
【答案】D
【解析】在△ABC中,∵∠ABC=90°,∴sin A=,∴BC=ACsin A=100×=60,∴AB==80.
9.在Rt△ABC中,∠C=90°,sin A=,BC=20,则△ABC的面积为( )
A.80 B.100 C.120 D.150
【答案】D
【解析】在Rt△ABC中,∵∠C=90°,sin A==,∴AB==25,∴AC===15,∴△ABC的面积为AC×BC=×15×20=150.
10.【2020·扬州】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为( A )
A. B. C. D.
第10题图 第11题图 第12题图
11.【攀枝花中考】如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( D )
A. B. C. D.
12.如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,,则sinA的值为( B )
A. B. C. D.
二、填空题
13.(1)如图,在Rt△ABC中,∠C=90°,我们把锐角A的________与________的比叫做∠A的正弦,记作________,即sin A==_______
【答案】对边 斜边 sin A 对边
(2)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则sinA=________,a=________,c=________,b2=__________.
【答案】 c·sinA c2-a2
第13(1)题图 第16题图 第17题图 第18题图
14.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是____.
【答案】
15.在Rt△ABC中,∠C=90°,AB=3BC,则sin B= .
16.已知AE,CF是锐角三角形ABC的两条高.若AE∶CF=3∶2,则sin∠BAC∶sin∠ACB= .
【答案】2∶3
【解析】根据题意,画出图形(如图).∵sin∠BAC=,sin∠ACB=,AE∶CF=3∶2,
∴sin∠BAC∶sin∠ACB==FC∶AE=2∶3.
17.如图,☉O是△ABC的外接圆,AD是☉O的直径,若☉O的半径是4,sinB=,则线段AC的长为 .
【答案】2
【解析】如图,连接CD,∵AD是☉O的直径,∴∠ACD=90°.∵∠D=∠B,
∴sin D=sin B=.在Rt△ACD中,sin D==,∴AC=AD=×8=2.
归纳总结
利用等角转换法求锐角三角函数值
利用等角转换法,把要求的角转化为与其相等的角,找相等角的方法有多种,可以借助平行线、等腰三角形、三角形全等(相似)和圆等知识来解决,要根据题目的条件灵活选用方法.
18.如图,在△ABC中,∠C=90°,∠A=∠CBD.若sin A=,AB=5,则CD= .
三、解答题
19.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)sin B可以写为哪两条线段之比?
解:∵CD⊥AB,∠ACB=90°,
∴∠ACD+∠A=90°,∠B+∠A=90°. ∴∠ACD=∠B.
∵在Rt△ADC中,sin∠ACD=,∴sin B=.
在Rt△BDC中,sin B=;
在Rt△BAC中,sin B=,∴sin B===.
(2)若AC=5,CD=3,求sin B的值.
解:在Rt△ADC中,AD===4,
∴sin B==.
20.如图,AB与⊙O相切于点C,OA=OB,⊙O的直径是4,AB=8.
(1)求OB的长;
解:由题意可知,OC=2.
∵AB与⊙O相切于点C,∴OC⊥AB.
∵OA=OB,∴AC=BC=4.
在Rt△OBC中,由勾股定理得OB===2.
(2)求sinA的值.
解:在Rt△OAC中,sinA===.
21.已知a,b,c分别是△ABC中∠A,∠B,∠C的对边,且满足等式b2=(c+a)(c-a),5b-4c=0,求sinA+sinB的值.
解:∵b2=(c+a)(c-a),
∴b2=c2-a2,即a2+b2=c2,
∴△ABC是以c为斜边的Rt△ABC.
∵5b-4c=0,∴,
设b=4k,则c=5k,∴a=3k,
∴sinA+sinB=.
22.【中考·潍坊】如图,点M是正方形ABCD的边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°.∴∠BAF+∠DAE=90°.
∵DE⊥AM,BF⊥AM,∴∠DEA=∠AFB=90°.
∴∠ADE+∠DAE=90°,∴∠BAF=∠ADE.
在△DEA和△AFB中,
∴△DEA≌△AFB.∴AE=BF.
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
解:设AE=x,则BF=x.
∵△DEA≌△AFB,∴DE=AF=2.
∵四边形ABED的面积为24,
∴AE·BF+AE·ED=x2+×2x=24,
解得x1=6,x2=-8(舍去).
∴AE=BF=6.
∴EF=AE-AF=6-2=4.
在Rt△EFB中,BE===2 ,
∴sin ∠EBF===.
23.【2021·随州】如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
证明:如图,连接OD.
∵DE是⊙O的切线,∴OD⊥DE.
∵BC⊥DE,∴OD∥BC.
∴∠ODA=∠C.
∵OA=OD,∴∠ODA=∠A.
∴∠A=∠C.∴AB=BC.
(2)若⊙O的直径为9,sin A=.
①求线段BF的长;
解:如图,连接BD,则∠ADB=90°.
在Rt△ABD中,∵sin A==,AB=9,∴BD=3.
∵OB=OD,∴∠ODB=∠OBD.
∵∠OBD+∠A=∠FDB+∠ODB=90°,
∴∠A=∠FDB,∴sin A=sin∠FDB.
在Rt△BDF中,∵sin∠BDF==,
∴BF=1.
②求线段BE的长.
解:由(1)知OD∥BF,∴∠EBF=∠EOD.
又∵∠BEF=∠OED,∴△EBF∽△EOD.
∴=,即=,
解得BE=.
24.【沈阳中考】如图,在△ABC中,以BC为直径的☉O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EF是☉O的切线;
(2)若sin∠EGC=,☉O的半径是3,求AF的长.
解:(1)连接OE.∴∠EOG=2∠C.
∵∠ABG=2∠C,∴∠EOG=∠ABG,∴AB∥OE.
∵EF⊥AB,∴EF⊥OE.
又∵OE是☉O的半径,∴EF是☉O的切线.
(2)∵∠ABG=2∠C,∠ABG=∠C+∠A,
∴∠A=∠C,∴AB=BC=6.
在Rt△OEG中,sin ∠EGC=,
∴OG==5,∴BG=OG-OB=2.
在Rt△FGB中,sin ∠EGC=,
∴BF=BG·sin ∠EGC=2×,
∴AF=AB-BF=6-.
第1课时 正 弦
一、选择题
1.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sin B的值为( )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,sinA=,AC=4,则AB的长为( )
A.2 B.4 C.6 D.8
3.【2021·桂林】如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
第3题图 第5题图 第6题图 第7题图
4.在Rt△ABC中,如果各边长度都扩大2倍,那么锐角A的正弦值( )
A.没有变化 B.扩大2倍 C.缩小2倍 D.不能确定
5.如图,在2×2的正方形网格中,以格点为顶点的△ABC的面积等于,则sin∠CAB的值为( )
A. B. C. D.
6.【2020·聊城】如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列各组线段的比不能表示sin∠BCD的是( )
A. B. C. D.
8.【2021·云南】在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )
A. B. C.60 D.80
9.在Rt△ABC中,∠C=90°,sin A=,BC=20,则△ABC的面积为( )
A.80 B.100 C.120 D.150
10.【2020·扬州】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为( )
A. B. C. D.
第10题图 第11题图 第12题图
11.【攀枝花中考】如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
12.如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,,则sinA的值为( )
A. B. C. D.
二、填空题
13.(1)如图,在Rt△ABC中,∠C=90°,我们把锐角A的________与________的比叫做∠A的正弦,记作________,即sin A==_______
(2)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则sinA=________,a=________,c=________,b2=__________.
第13(1)题图 第16题图 第17题图 第18题图
14.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是____.
15.在Rt△ABC中,∠C=90°,AB=3BC,则sin B= .
16.已知AE,CF是锐角三角形ABC的两条高.若AE∶CF=3∶2,则sin∠BAC∶sin∠ACB= .
17.如图,☉O是△ABC的外接圆,AD是☉O的直径,若☉O的半径是4,sinB=,则线段AC的长为 .
归纳总结
利用等角转换法求锐角三角函数值
利用等角转换法,把要求的角转化为与其相等的角,找相等角的方法有多种,可以借助平行线、等腰三角形、三角形全等(相似)和圆等知识来解决,要根据题目的条件灵活选用方法.
18.如图,在△ABC中,∠C=90°,∠A=∠CBD.若sin A=,AB=5,则CD= .
三、解答题
19.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)sin B可以写为哪两条线段之比?
(2)若AC=5,CD=3,求sin B的值.
20.如图,AB与⊙O相切于点C,OA=OB,⊙O的直径是4,AB=8.
(1)求OB的长;
(2)求sinA的值.
21.已知a,b,c分别是△ABC中∠A,∠B,∠C的对边,且满足等式b2=(c+a)(c-a),5b-4c=0,求sinA+sinB的值.
22.【中考·潍坊】如图,点M是正方形ABCD的边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
23.【2021·随州】如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
(2)若⊙O的直径为9,sin A=.
①求线段BF的长;
②求线段BE的长.
24.【沈阳中考】如图,在△ABC中,以BC为直径的☉O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EF是☉O的切线;
(2)若sin∠EGC=,☉O的半径是3,求AF的长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2020·河池】在Rt△ABC中,∠C=90°,BC=5,AC=12,则sin B的值为( D )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,sinA=,AC=4,则AB的长为( C )
A.2 B.4 C.6 D.8
3.【2021·桂林】如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
【答案】D
【解析】如图,过点P作PM⊥x轴于点M,∵P(3,4),∴OM=3,PM=4,∴OP==5,∴sin α==.
第3题图 第5题图 第6题图 第7题图
4.在Rt△ABC中,如果各边长度都扩大2倍,那么锐角A的正弦值( )
A.没有变化 B.扩大2倍 C.缩小2倍 D.不能确定
【答案】A
【解析】若Rt△ABC的各边长度都扩大2倍,则所得新三角形与原三角形相似,故锐角A大小不变,其正弦值也没有变化.
5.如图,在2×2的正方形网格中,以格点为顶点的△ABC的面积等于,则sin ∠CAB的值为( B )
A. B. C. D.
6.【2020·聊城】如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( D )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列各组线段的比不能表示sin∠BCD的是( )
A. B. C. D.
【答案】C
【解析】∵CD⊥AB,∴∠CDA=90°,∴∠A+∠ACD=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°,
∴∠BCD=∠A.∵sin∠BCD=,sin A==,∴A项、B项、D项都能表示sin∠BCD.
8.【2021·云南】在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )
A. B. C.60 D.80
【答案】D
【解析】在△ABC中,∵∠ABC=90°,∴sin A=,∴BC=ACsin A=100×=60,∴AB==80.
9.在Rt△ABC中,∠C=90°,sin A=,BC=20,则△ABC的面积为( )
A.80 B.100 C.120 D.150
【答案】D
【解析】在Rt△ABC中,∵∠C=90°,sin A==,∴AB==25,∴AC===15,∴△ABC的面积为AC×BC=×15×20=150.
10.【2020·扬州】如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为( A )
A. B. C. D.
第10题图 第11题图 第12题图
11.【攀枝花中考】如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( D )
A. B. C. D.
12.如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,,则sinA的值为( B )
A. B. C. D.
二、填空题
13.(1)如图,在Rt△ABC中,∠C=90°,我们把锐角A的________与________的比叫做∠A的正弦,记作________,即sin A==_______
【答案】对边 斜边 sin A 对边
(2)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则sinA=________,a=________,c=________,b2=__________.
【答案】 c·sinA c2-a2
第13(1)题图 第16题图 第17题图 第18题图
14.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是____.
【答案】
15.在Rt△ABC中,∠C=90°,AB=3BC,则sin B= .
16.已知AE,CF是锐角三角形ABC的两条高.若AE∶CF=3∶2,则sin∠BAC∶sin∠ACB= .
【答案】2∶3
【解析】根据题意,画出图形(如图).∵sin∠BAC=,sin∠ACB=,AE∶CF=3∶2,
∴sin∠BAC∶sin∠ACB==FC∶AE=2∶3.
17.如图,☉O是△ABC的外接圆,AD是☉O的直径,若☉O的半径是4,sinB=,则线段AC的长为 .
【答案】2
【解析】如图,连接CD,∵AD是☉O的直径,∴∠ACD=90°.∵∠D=∠B,
∴sin D=sin B=.在Rt△ACD中,sin D==,∴AC=AD=×8=2.
归纳总结
利用等角转换法求锐角三角函数值
利用等角转换法,把要求的角转化为与其相等的角,找相等角的方法有多种,可以借助平行线、等腰三角形、三角形全等(相似)和圆等知识来解决,要根据题目的条件灵活选用方法.
18.如图,在△ABC中,∠C=90°,∠A=∠CBD.若sin A=,AB=5,则CD= .
三、解答题
19.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)sin B可以写为哪两条线段之比?
解:∵CD⊥AB,∠ACB=90°,
∴∠ACD+∠A=90°,∠B+∠A=90°. ∴∠ACD=∠B.
∵在Rt△ADC中,sin∠ACD=,∴sin B=.
在Rt△BDC中,sin B=;
在Rt△BAC中,sin B=,∴sin B===.
(2)若AC=5,CD=3,求sin B的值.
解:在Rt△ADC中,AD===4,
∴sin B==.
20.如图,AB与⊙O相切于点C,OA=OB,⊙O的直径是4,AB=8.
(1)求OB的长;
解:由题意可知,OC=2.
∵AB与⊙O相切于点C,∴OC⊥AB.
∵OA=OB,∴AC=BC=4.
在Rt△OBC中,由勾股定理得OB===2.
(2)求sinA的值.
解:在Rt△OAC中,sinA===.
21.已知a,b,c分别是△ABC中∠A,∠B,∠C的对边,且满足等式b2=(c+a)(c-a),5b-4c=0,求sinA+sinB的值.
解:∵b2=(c+a)(c-a),
∴b2=c2-a2,即a2+b2=c2,
∴△ABC是以c为斜边的Rt△ABC.
∵5b-4c=0,∴,
设b=4k,则c=5k,∴a=3k,
∴sinA+sinB=.
22.【中考·潍坊】如图,点M是正方形ABCD的边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°.∴∠BAF+∠DAE=90°.
∵DE⊥AM,BF⊥AM,∴∠DEA=∠AFB=90°.
∴∠ADE+∠DAE=90°,∴∠BAF=∠ADE.
在△DEA和△AFB中,
∴△DEA≌△AFB.∴AE=BF.
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
解:设AE=x,则BF=x.
∵△DEA≌△AFB,∴DE=AF=2.
∵四边形ABED的面积为24,
∴AE·BF+AE·ED=x2+×2x=24,
解得x1=6,x2=-8(舍去).
∴AE=BF=6.
∴EF=AE-AF=6-2=4.
在Rt△EFB中,BE===2 ,
∴sin ∠EBF===.
23.【2021·随州】如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
证明:如图,连接OD.
∵DE是⊙O的切线,∴OD⊥DE.
∵BC⊥DE,∴OD∥BC.
∴∠ODA=∠C.
∵OA=OD,∴∠ODA=∠A.
∴∠A=∠C.∴AB=BC.
(2)若⊙O的直径为9,sin A=.
①求线段BF的长;
解:如图,连接BD,则∠ADB=90°.
在Rt△ABD中,∵sin A==,AB=9,∴BD=3.
∵OB=OD,∴∠ODB=∠OBD.
∵∠OBD+∠A=∠FDB+∠ODB=90°,
∴∠A=∠FDB,∴sin A=sin∠FDB.
在Rt△BDF中,∵sin∠BDF==,
∴BF=1.
②求线段BE的长.
解:由(1)知OD∥BF,∴∠EBF=∠EOD.
又∵∠BEF=∠OED,∴△EBF∽△EOD.
∴=,即=,
解得BE=.
24.【沈阳中考】如图,在△ABC中,以BC为直径的☉O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EF是☉O的切线;
(2)若sin∠EGC=,☉O的半径是3,求AF的长.
解:(1)连接OE.∴∠EOG=2∠C.
∵∠ABG=2∠C,∴∠EOG=∠ABG,∴AB∥OE.
∵EF⊥AB,∴EF⊥OE.
又∵OE是☉O的半径,∴EF是☉O的切线.
(2)∵∠ABG=2∠C,∠ABG=∠C+∠A,
∴∠A=∠C,∴AB=BC=6.
在Rt△OEG中,sin ∠EGC=,
∴OG==5,∴BG=OG-OB=2.
在Rt△FGB中,sin ∠EGC=,
∴BF=BG·sin ∠EGC=2×,
∴AF=AB-BF=6-.
