28.2.1 解直角三角形同步练习(含答案)
文档属性
| 名称 | 28.2.1 解直角三角形同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 16:16:50 | ||
图片预览



文档简介
28.2 解直角三角形及其应用
28.2.1 解直角三角形
一、选择题
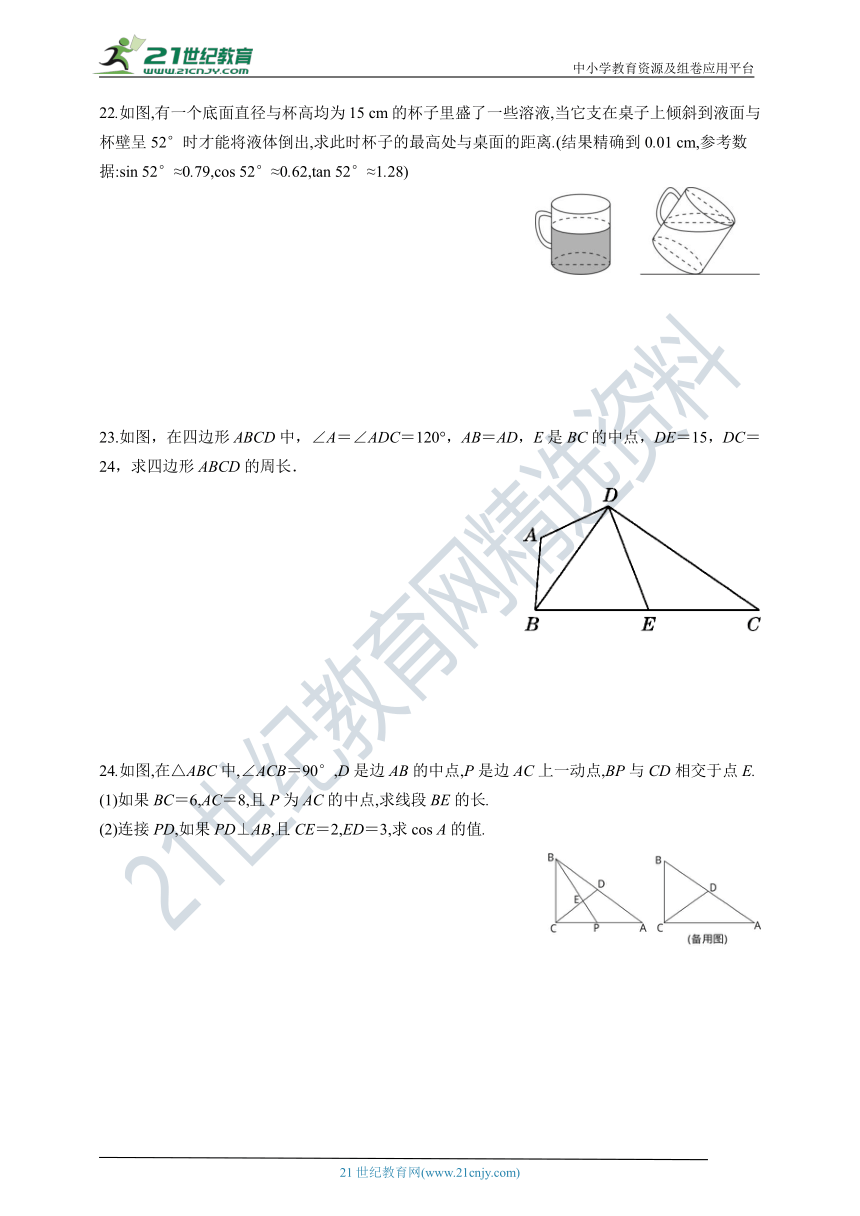
1.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cos A=( )
A. B. C. D.
第1题图 第2题图 第3题图 第4题图
2.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
3.如图,在正方形网格中,若△ABC的三个顶点都在格点上,则tan∠BAC的值是( )
A. B. C. D.
4.若△ABC在网格中的位置如图,则cos B的值为( )
A. B. C. D.2
5.如图,在正方形网格中,若△ABC的三个顶点均在格点上,则sin∠ABC的值为( )
A. B. C. D.2
第5题图 第6题图 第9题图
6.如图,在Rt△ABC中,若∠C=90°,AB=4,∠A=30°,则AC的长为( )
A.2 B.3 C. D.2
7.已知一个直角三角形的周长是4+2,斜边上中线的长为2,则这个三角形的面积为( )
A.5 B.2 C. D.1
8.在Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C=90°,∠A=30°,斜边上的高为1,则Rt△ABC的三边长分别为( )
A.a=,b=2,c= B.a=,b=2,c=
C.a=2,b=,c= D.a=2,b=2,c=4
9.【2021·玉林】如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2 C.h1>h2 D.以上都有可能
10.【中考·湘西州】如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.10 B.8 C.4 D.2
第10题图 第11题图 第12题图
11.【2021·黑龙江】如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
12.如图,菱形ABCD的周长为40 cm,DE⊥AB,垂足为E,sin A=,则下列结论:①DE=6 cm;②BE=2 cm;③菱形ABCD的面积为60 cm2;④BD=4 cm.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
13.解直角三角形的依据:
如图,在Rt△ABC中,∠C=90°,则有:
(1)三边之间的关系:__________;
(2)两锐角之间的关系:______________________________;
(3)边角之间的关系:
sinA=______,sinB=______,
cosA=______,cosB=______,
tanA=______,tanB=______.
14.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=7,c=7,则b= ,∠A= ,∠B= .
15.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=2,tan ∠BCD=,则AB= .
第15题图 第16题图 第17题图
16.【中考·盐城】如图,在△ABC中,BC=+,∠C=45°,AB=AC,则AC的长为________.
17.【2021·海南】如图,△ABC的顶点B,C的坐标分别是(1,0),(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是____________.
18.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为 .
三、解答题
19.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=45°,c=14;
(2)a=,∠A=60°.
20.如图,在△ABC中,∠ACB=90°,D为AB的中点,连接CD.若BC=4,CD=3,求sin ∠ACD的值.
21.如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan B=.
(1)求AD的长;
(2)求sin α的值.
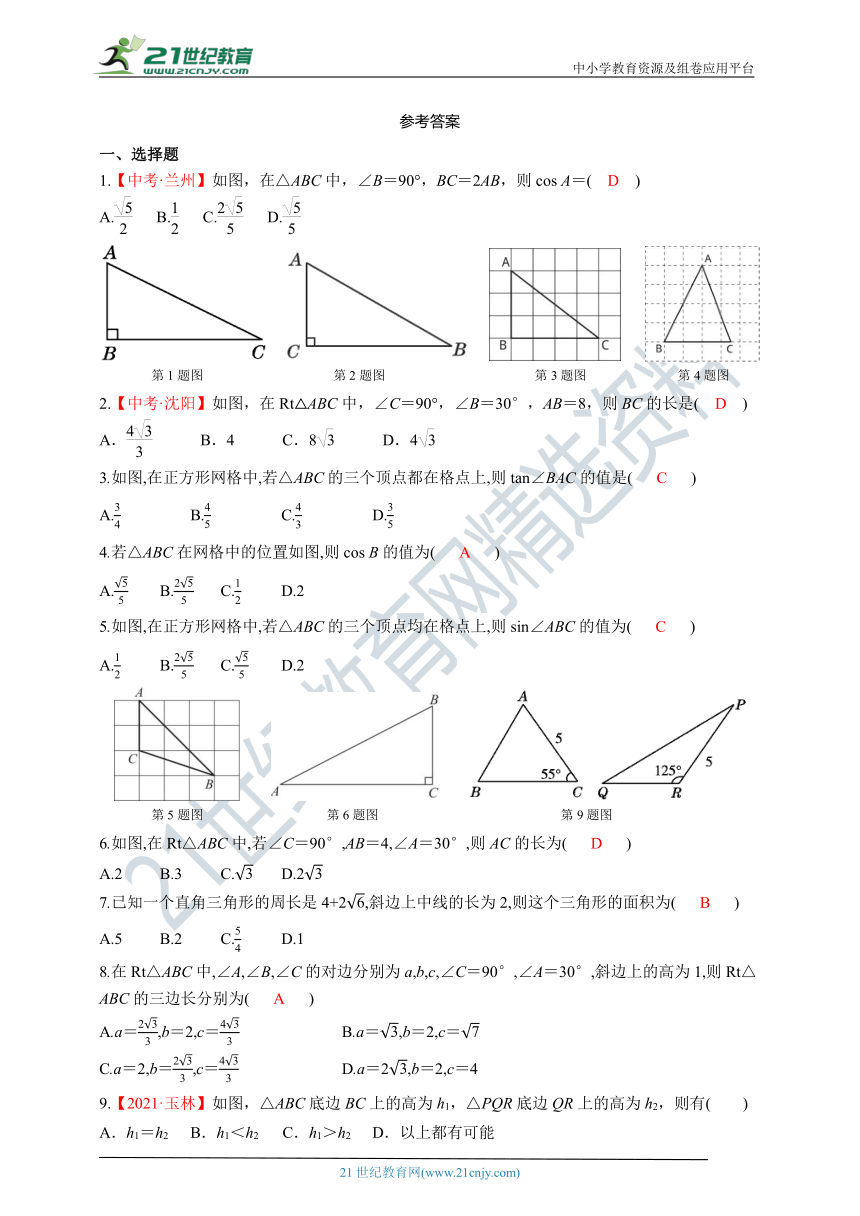
22.如图,有一个底面直径与杯高均为15 cm的杯子里盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈52°时才能将液体倒出,求此时杯子的最高处与桌面的距离.(结果精确到0.01 cm,参考数据:sin 52°≈0.79,cos 52°≈0.62,tan 52°≈1.28)
23.如图,在四边形ABCD中,∠A=∠ADC=120°,AB=AD,E是BC的中点,DE=15,DC=24,求四边形ABCD的周长.
24.如图,在△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长.
(2)连接PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cos A=( D )
A. B. C. D.
第1题图 第2题图 第3题图 第4题图
2.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( D )
A. B.4 C.8 D.4
3.如图,在正方形网格中,若△ABC的三个顶点都在格点上,则tan∠BAC的值是( C )
A. B. C. D.
4.若△ABC在网格中的位置如图,则cos B的值为( A )
A. B. C. D.2
5.如图,在正方形网格中,若△ABC的三个顶点均在格点上,则sin∠ABC的值为( C )
A. B. C. D.2
第5题图 第6题图 第9题图
6.如图,在Rt△ABC中,若∠C=90°,AB=4,∠A=30°,则AC的长为( D )
A.2 B.3 C. D.2
7.已知一个直角三角形的周长是4+2,斜边上中线的长为2,则这个三角形的面积为( B )
A.5 B.2 C. D.1
8.在Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C=90°,∠A=30°,斜边上的高为1,则Rt△ABC的三边长分别为( A )
A.a=,b=2,c= B.a=,b=2,c=
C.a=2,b=,c= D.a=2,b=2,c=4
9.【2021·玉林】如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2 C.h1>h2 D.以上都有可能
【点拨】如图,分别作出△ABC底边BC上的高AD(即h1),△PQR底边QR上的高PE(即h2).
在Rt△ADC中,h1=AD=5×sin 55°;
在Rt△PER中,h2=PE=5×sin 55°,∴h1=h2.
10.【中考·湘西州】如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( D )
A.10 B.8 C.4 D.2
第10题图 第11题图 第12题图
11.【2021·黑龙江】如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( B )
A.1 B.2 C. D.
【点拨】过点D作DM⊥BC,交CB的延长线于点M,如图.
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==.
∵AB=2BD,∴===.
在Rt△CDM中,
tan∠MCD==,
设DM=2k,则CM=3k.
又∵==,∴BC=2k,AC=4k,
∴==2,故选B.
12.如图,菱形ABCD的周长为40 cm,DE⊥AB,垂足为E,sin A=,则下列结论:①DE=6 cm;②BE=2 cm;③菱形ABCD的面积为60 cm2;④BD=4 cm.其中正确的结论有( B )
A.4个 B.3个 C.2个 D.1个
二、填空题
13.解直角三角形的依据:
如图,在Rt△ABC中,∠C=90°,则有:
(1)三边之间的关系:__________;
【答案】a2+b2=c2
(2)两锐角之间的关系:______________________________;
【答案】∠A+∠B=90°
(3)边角之间的关系:
sinA=______,sinB=______,
cosA=______,cosB=______,
tanA=______,tanB=______.
【答案】
14.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=7,c=7,则b= 7 ,∠A= 45° ,∠B= 45° .
15.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=2,tan ∠BCD=,则AB=3 .
第15题图 第16题图 第17题图
16.【中考·盐城】如图,在△ABC中,BC=+,∠C=45°,AB=AC,则AC的长为________.
【点拨】作AD⊥BC,垂足为点D.设AC=x,则AB=x.
在Rt△ACD中,AD=AC·sin C=x,CD=AC·cos C=x.
在Rt△ABD中,AB=x,AD=x,
∴BD==x.
∴BC=BD+CD=x+x=+.
∴x=2,即AC=2.
【答案】2
17.【2021·海南】如图,△ABC的顶点B,C的坐标分别是(1,0),(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是____________.
【点拨】如图,过点A作AG⊥x轴,垂足为点G.
∵B,C的坐标分别是(1,0),(0,),∴OC=,OB=1.
∴BC==2.
∵∠ABC=90°,∠BAC=30°,∴AB===2.
∵∠ABG+∠CBO=90°,∠BCO+∠CBO=90°,
∴∠ABG=∠BCO.
∴sin∠ABG==sin∠BCO==,cos∠ABG==cos∠BCO==.
∴AG=,BG=3.
∴OG=1+3=4.
∴顶点A的坐标是(4,).
【答案】(4,)
18.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为 2或4 .
三、解答题
19.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=45°,c=14;
(2)a=,∠A=60°.
解:(1)∠A=45°,a=b=.
(2)∠B=30°,b=.
20.如图,在△ABC中,∠ACB=90°,D为AB的中点,连接CD.若BC=4,CD=3,求sin ∠ACD的值.
解:∵∠ACB=90°,D为AB的中点,∴CD=AB=AD,
∴AB=2CD=6,∠ACD=∠A,
∴sin ∠ACD=sin ∠A=.
21.如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan B=.
(1)求AD的长;
(2)求sin α的值.
解:(1)由tan B=可设AC=3x,BC=4x.
又∵AC2+BC2=AB2,∴(3x)2+(4x)2=52,
解得x=1或x=-1(舍去),∴AC=3,BC=4.
∵BD=1,∴CD=3,∴AD=.
(2)过点D作DE⊥AB于点E.
∵,
∴sin α=.
22.如图,有一个底面直径与杯高均为15 cm的杯子里盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈52°时才能将液体倒出,求此时杯子的最高处与桌面的距离.(结果精确到0.01 cm,参考数据:sin 52°≈0.79,cos 52°≈0.62,tan 52°≈1.28)
解:如图,过点A作AE⊥BC,交BC于点E,过点C作CF⊥PD,交PD所在直线于点F,那么AE+CF的长即为此时杯子的最高处与桌面的距离.
在Rt△ACE中,AE=AC·cos ∠CAE=15×cos 52°≈15×0.62=9.3(cm).
在Rt△DCF中,CF=CD·sin ∠CDF=15×sin 52°≈15×0.79=11.85(cm),
所以AE+CF=9.3+11.85=21.15(cm).
答:此时杯子的最高处与桌面的距离约为21.15 cm.
23.如图,在四边形ABCD中,∠A=∠ADC=120°,AB=AD,E是BC的中点,DE=15,DC=24,求四边形ABCD的周长.
解:如图,过点A作AF⊥BD于点F.
∵∠BAD=120°,AB=AD,
∴∠ABD=∠ADB=30°.
∵∠ADC=120°,
∴∠BDC=∠ADC-∠ADB=120°-30°=90°.
在Rt△BDC中,∠BDC=90°,E是BC的中点,DE=15,
∴BC=2DE=30.
∴BD===18.
∵AD=AB,AF⊥BD,∴DF=BD=×18=9.
在Rt△AFD中,∵∠AFD=90°,∠ADB=30°,
∴AD=AB===6.
∴四边形ABCD的周长为AB+BC+CD+AD=6+30+24+6=54+12.
24.如图,在△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长.
(2)连接PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值.
解:(1)∵P为AC的中点,AC=8,∴CP=4.
∵∠ACB=90°,BC=6,∴BP=2.
∵D是边AB的中点,P为AC的中点,
∴点E是△ABC的重心,
∴BE=.
(2)如图,过点B作BF∥CA,交CD的延长线于点F,∴.
∵BD=DA,∴FD=DC,BF=AC.
∵CE=2,ED=3,∴CD=5,∴EF=8,
∴.
设CP=k,∴PA=3k.
∵PD⊥AB,D是边AB的中点,∴PA=PB=3k,
∴BC=2k.
∵AC=4k,∴cos A=.
28.2.1 解直角三角形
一、选择题
1.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cos A=( )
A. B. C. D.
第1题图 第2题图 第3题图 第4题图
2.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
3.如图,在正方形网格中,若△ABC的三个顶点都在格点上,则tan∠BAC的值是( )
A. B. C. D.
4.若△ABC在网格中的位置如图,则cos B的值为( )
A. B. C. D.2
5.如图,在正方形网格中,若△ABC的三个顶点均在格点上,则sin∠ABC的值为( )
A. B. C. D.2
第5题图 第6题图 第9题图
6.如图,在Rt△ABC中,若∠C=90°,AB=4,∠A=30°,则AC的长为( )
A.2 B.3 C. D.2
7.已知一个直角三角形的周长是4+2,斜边上中线的长为2,则这个三角形的面积为( )
A.5 B.2 C. D.1
8.在Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C=90°,∠A=30°,斜边上的高为1,则Rt△ABC的三边长分别为( )
A.a=,b=2,c= B.a=,b=2,c=
C.a=2,b=,c= D.a=2,b=2,c=4
9.【2021·玉林】如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2 C.h1>h2 D.以上都有可能
10.【中考·湘西州】如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.10 B.8 C.4 D.2
第10题图 第11题图 第12题图
11.【2021·黑龙江】如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
12.如图,菱形ABCD的周长为40 cm,DE⊥AB,垂足为E,sin A=,则下列结论:①DE=6 cm;②BE=2 cm;③菱形ABCD的面积为60 cm2;④BD=4 cm.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
13.解直角三角形的依据:
如图,在Rt△ABC中,∠C=90°,则有:
(1)三边之间的关系:__________;
(2)两锐角之间的关系:______________________________;
(3)边角之间的关系:
sinA=______,sinB=______,
cosA=______,cosB=______,
tanA=______,tanB=______.
14.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=7,c=7,则b= ,∠A= ,∠B= .
15.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=2,tan ∠BCD=,则AB= .
第15题图 第16题图 第17题图
16.【中考·盐城】如图,在△ABC中,BC=+,∠C=45°,AB=AC,则AC的长为________.
17.【2021·海南】如图,△ABC的顶点B,C的坐标分别是(1,0),(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是____________.
18.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为 .
三、解答题
19.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=45°,c=14;
(2)a=,∠A=60°.
20.如图,在△ABC中,∠ACB=90°,D为AB的中点,连接CD.若BC=4,CD=3,求sin ∠ACD的值.
21.如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan B=.
(1)求AD的长;
(2)求sin α的值.
22.如图,有一个底面直径与杯高均为15 cm的杯子里盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈52°时才能将液体倒出,求此时杯子的最高处与桌面的距离.(结果精确到0.01 cm,参考数据:sin 52°≈0.79,cos 52°≈0.62,tan 52°≈1.28)
23.如图,在四边形ABCD中,∠A=∠ADC=120°,AB=AD,E是BC的中点,DE=15,DC=24,求四边形ABCD的周长.
24.如图,在△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长.
(2)连接PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【中考·兰州】如图,在△ABC中,∠B=90°,BC=2AB,则cos A=( D )
A. B. C. D.
第1题图 第2题图 第3题图 第4题图
2.【中考·沈阳】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( D )
A. B.4 C.8 D.4
3.如图,在正方形网格中,若△ABC的三个顶点都在格点上,则tan∠BAC的值是( C )
A. B. C. D.
4.若△ABC在网格中的位置如图,则cos B的值为( A )
A. B. C. D.2
5.如图,在正方形网格中,若△ABC的三个顶点均在格点上,则sin∠ABC的值为( C )
A. B. C. D.2
第5题图 第6题图 第9题图
6.如图,在Rt△ABC中,若∠C=90°,AB=4,∠A=30°,则AC的长为( D )
A.2 B.3 C. D.2
7.已知一个直角三角形的周长是4+2,斜边上中线的长为2,则这个三角形的面积为( B )
A.5 B.2 C. D.1
8.在Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C=90°,∠A=30°,斜边上的高为1,则Rt△ABC的三边长分别为( A )
A.a=,b=2,c= B.a=,b=2,c=
C.a=2,b=,c= D.a=2,b=2,c=4
9.【2021·玉林】如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2 C.h1>h2 D.以上都有可能
【点拨】如图,分别作出△ABC底边BC上的高AD(即h1),△PQR底边QR上的高PE(即h2).
在Rt△ADC中,h1=AD=5×sin 55°;
在Rt△PER中,h2=PE=5×sin 55°,∴h1=h2.
10.【中考·湘西州】如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( D )
A.10 B.8 C.4 D.2
第10题图 第11题图 第12题图
11.【2021·黑龙江】如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( B )
A.1 B.2 C. D.
【点拨】过点D作DM⊥BC,交CB的延长线于点M,如图.
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==.
∵AB=2BD,∴===.
在Rt△CDM中,
tan∠MCD==,
设DM=2k,则CM=3k.
又∵==,∴BC=2k,AC=4k,
∴==2,故选B.
12.如图,菱形ABCD的周长为40 cm,DE⊥AB,垂足为E,sin A=,则下列结论:①DE=6 cm;②BE=2 cm;③菱形ABCD的面积为60 cm2;④BD=4 cm.其中正确的结论有( B )
A.4个 B.3个 C.2个 D.1个
二、填空题
13.解直角三角形的依据:
如图,在Rt△ABC中,∠C=90°,则有:
(1)三边之间的关系:__________;
【答案】a2+b2=c2
(2)两锐角之间的关系:______________________________;
【答案】∠A+∠B=90°
(3)边角之间的关系:
sinA=______,sinB=______,
cosA=______,cosB=______,
tanA=______,tanB=______.
【答案】
14.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=7,c=7,则b= 7 ,∠A= 45° ,∠B= 45° .
15.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=2,tan ∠BCD=,则AB=3 .
第15题图 第16题图 第17题图
16.【中考·盐城】如图,在△ABC中,BC=+,∠C=45°,AB=AC,则AC的长为________.
【点拨】作AD⊥BC,垂足为点D.设AC=x,则AB=x.
在Rt△ACD中,AD=AC·sin C=x,CD=AC·cos C=x.
在Rt△ABD中,AB=x,AD=x,
∴BD==x.
∴BC=BD+CD=x+x=+.
∴x=2,即AC=2.
【答案】2
17.【2021·海南】如图,△ABC的顶点B,C的坐标分别是(1,0),(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是____________.
【点拨】如图,过点A作AG⊥x轴,垂足为点G.
∵B,C的坐标分别是(1,0),(0,),∴OC=,OB=1.
∴BC==2.
∵∠ABC=90°,∠BAC=30°,∴AB===2.
∵∠ABG+∠CBO=90°,∠BCO+∠CBO=90°,
∴∠ABG=∠BCO.
∴sin∠ABG==sin∠BCO==,cos∠ABG==cos∠BCO==.
∴AG=,BG=3.
∴OG=1+3=4.
∴顶点A的坐标是(4,).
【答案】(4,)
18.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为 2或4 .
三、解答题
19.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=45°,c=14;
(2)a=,∠A=60°.
解:(1)∠A=45°,a=b=.
(2)∠B=30°,b=.
20.如图,在△ABC中,∠ACB=90°,D为AB的中点,连接CD.若BC=4,CD=3,求sin ∠ACD的值.
解:∵∠ACB=90°,D为AB的中点,∴CD=AB=AD,
∴AB=2CD=6,∠ACD=∠A,
∴sin ∠ACD=sin ∠A=.
21.如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tan B=.
(1)求AD的长;
(2)求sin α的值.
解:(1)由tan B=可设AC=3x,BC=4x.
又∵AC2+BC2=AB2,∴(3x)2+(4x)2=52,
解得x=1或x=-1(舍去),∴AC=3,BC=4.
∵BD=1,∴CD=3,∴AD=.
(2)过点D作DE⊥AB于点E.
∵,
∴sin α=.
22.如图,有一个底面直径与杯高均为15 cm的杯子里盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈52°时才能将液体倒出,求此时杯子的最高处与桌面的距离.(结果精确到0.01 cm,参考数据:sin 52°≈0.79,cos 52°≈0.62,tan 52°≈1.28)
解:如图,过点A作AE⊥BC,交BC于点E,过点C作CF⊥PD,交PD所在直线于点F,那么AE+CF的长即为此时杯子的最高处与桌面的距离.
在Rt△ACE中,AE=AC·cos ∠CAE=15×cos 52°≈15×0.62=9.3(cm).
在Rt△DCF中,CF=CD·sin ∠CDF=15×sin 52°≈15×0.79=11.85(cm),
所以AE+CF=9.3+11.85=21.15(cm).
答:此时杯子的最高处与桌面的距离约为21.15 cm.
23.如图,在四边形ABCD中,∠A=∠ADC=120°,AB=AD,E是BC的中点,DE=15,DC=24,求四边形ABCD的周长.
解:如图,过点A作AF⊥BD于点F.
∵∠BAD=120°,AB=AD,
∴∠ABD=∠ADB=30°.
∵∠ADC=120°,
∴∠BDC=∠ADC-∠ADB=120°-30°=90°.
在Rt△BDC中,∠BDC=90°,E是BC的中点,DE=15,
∴BC=2DE=30.
∴BD===18.
∵AD=AB,AF⊥BD,∴DF=BD=×18=9.
在Rt△AFD中,∵∠AFD=90°,∠ADB=30°,
∴AD=AB===6.
∴四边形ABCD的周长为AB+BC+CD+AD=6+30+24+6=54+12.
24.如图,在△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长.
(2)连接PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值.
解:(1)∵P为AC的中点,AC=8,∴CP=4.
∵∠ACB=90°,BC=6,∴BP=2.
∵D是边AB的中点,P为AC的中点,
∴点E是△ABC的重心,
∴BE=.
(2)如图,过点B作BF∥CA,交CD的延长线于点F,∴.
∵BD=DA,∴FD=DC,BF=AC.
∵CE=2,ED=3,∴CD=5,∴EF=8,
∴.
设CP=k,∴PA=3k.
∵PD⊥AB,D是边AB的中点,∴PA=PB=3k,
∴BC=2k.
∵AC=4k,∴cos A=.
