28.2.2.1 仰角、俯角同步练习(含答案)
文档属性
| 名称 | 28.2.2.1 仰角、俯角同步练习(含答案) | 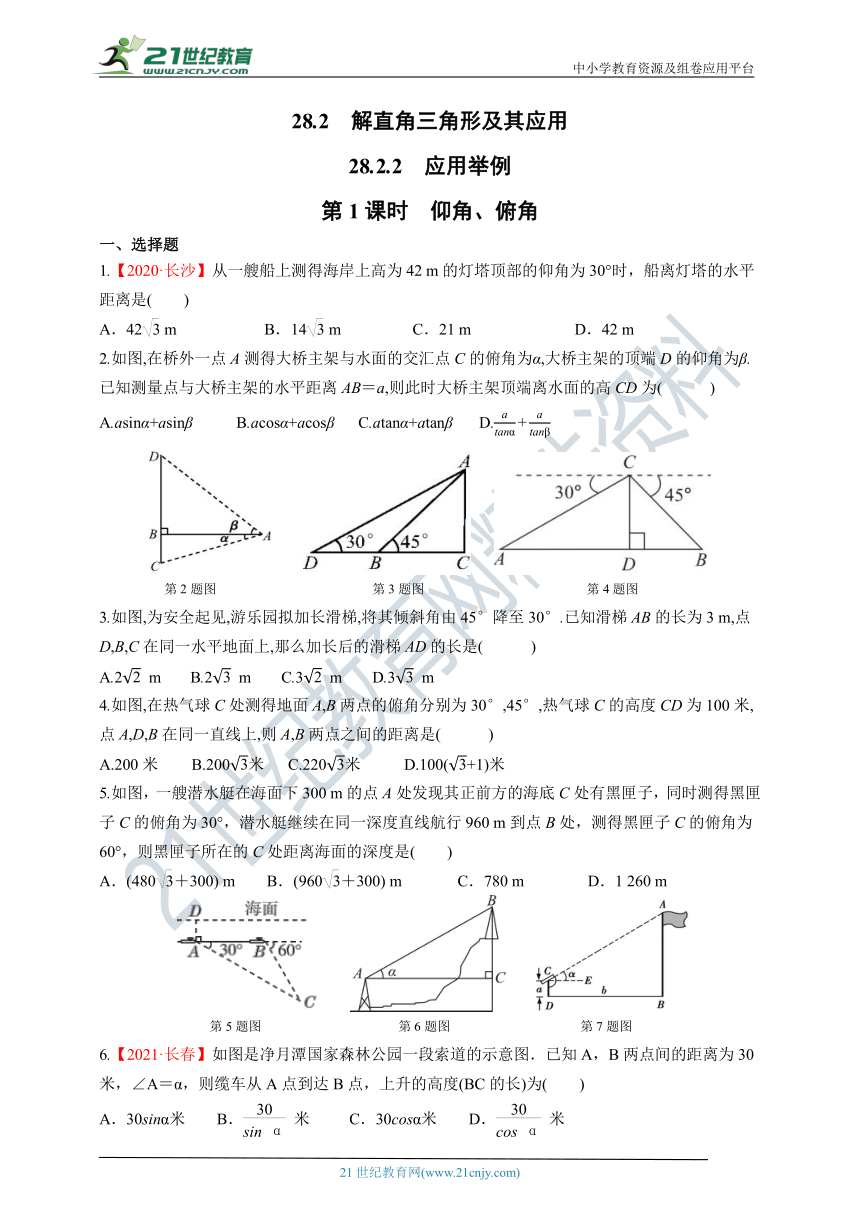 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 16:18:42 | ||
图片预览



文档简介
28.2 解直角三角形及其应用
28.2.2 应用举例
第1课时 仰角、俯角
一、选择题
1.【2020·长沙】从一艘船上测得海岸上高为42 m的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42 m B.14 m C.21 m D.42 m
2.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β.已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ C.atanα+atanβ D.
第2题图 第3题图 第4题图
3.如图,为安全起见,游乐园拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 m B.2 m C.3 m D.3 m
4.如图,在热气球C处测得地面A,B两点的俯角分别为30°,45°,热气球C的高度CD为100米,点A,D,B在同一直线上,则A,B两点之间的距离是( )
A.200米 B.200米 C.220米 D.100(+1)米
5.如图,一艘潜水艇在海面下300 m的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960 m到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( )
A.(480+300) m B.(960+300) m C.780 m D.1 260 m
第5题图 第6题图 第7题图
6.【2021·长春】如图是净月潭国家森林公园一段索道的示意图.已知A,B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米 B.米 C.30cosα米 D.米
7.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=a;(3)量得测角仪到旗杆的水平距离DB=b,利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.a+btan α B.a+bsin α C.a+ D.a+
8.如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,出于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为(参考数据:≈1.4,≈1.7)( )
A.7米 B.14米 C.20米 D.40米
第8题图 第9题图 第10题图
9.【2020·温州】如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tan α)米 B.米 C.(1.5+150sin α)米 D.米
10.【中考·长春】如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )
A.800sin α米 B.800tan α米 C.米 D.米
11.【2021·重庆A卷】如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度i=1:1.25.若,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为( )(参考数据:≈1.41,≈1.73)
A.9.0m B.12.8m C.13.1m D.22.7m
第11题图 第12题图
12.【2021·重庆B卷】如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为( )
(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
二、填空题
13.如图,甲、乙是两个高度相等且底面直径之比为1∶2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是 cm.
第13题图 第14题图 第15题图
14.【2021·天门】如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为3 m/s,从A处沿水平方向飞行至B处需10 s.同时在地面C处分别测得A处的仰角为75°,B处的仰角为30°,则这架无人机的飞行高度大约是________m(≈1.732,结果保留整数).
15.【2021·赤峰】某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头C处的高度CD为238米,点A,D,B在同一直线上,则雪道AB的长度约为________米(结果保留整数,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
16.【2021·广西北部湾经济区】如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为___________米(结果保留根号).
第16题图 第17题图 第18题图
17.【2021·黄冈】如图,建筑物BC上有一高为8 m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为________m(结果保留小数点后一位;参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33).
18.如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200 米到达湖边点N处,测得塔尖点A在湖中的倒影点A'的俯角∠A'NB为45°,则电视塔AB的高度为 米.(结果保留根号)
三、解答题
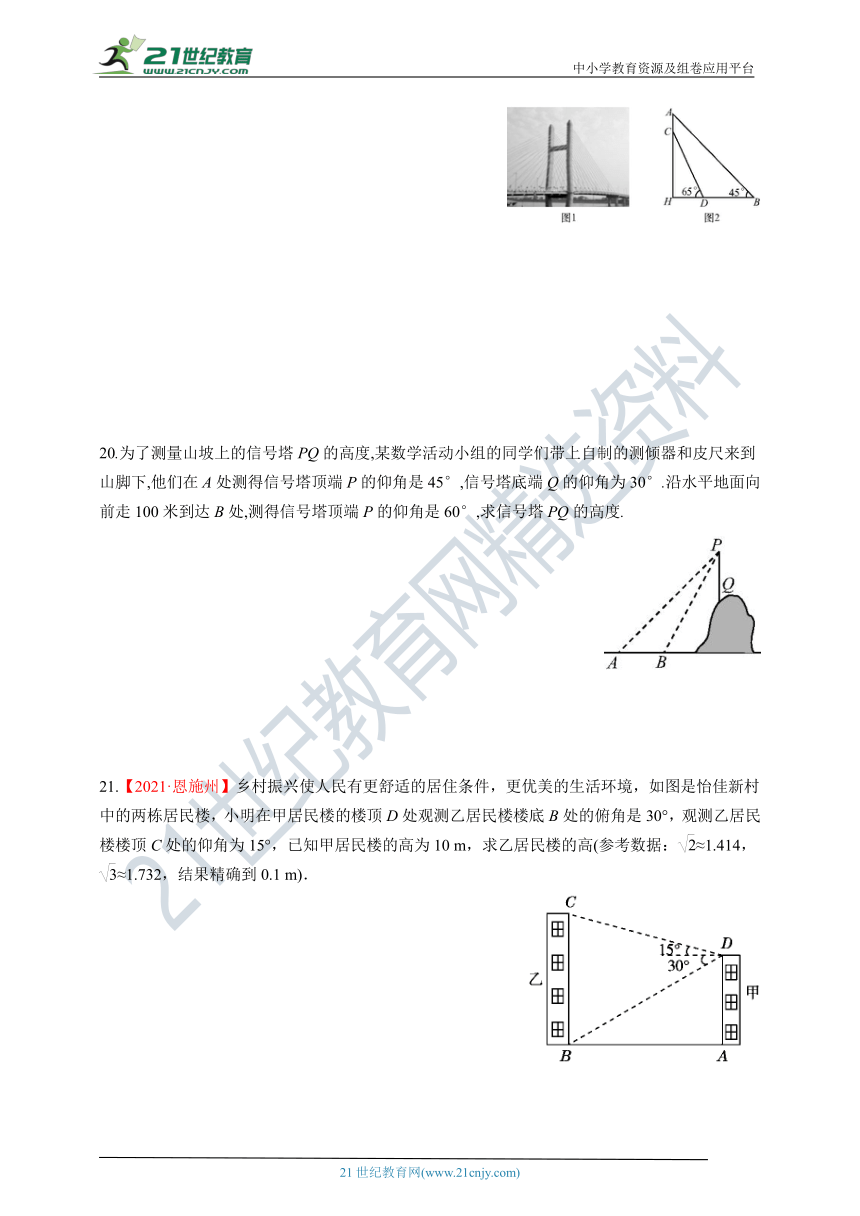
19.高淳固城湖大桥采用H型塔形斜拉桥结构(如图1),图2是从图1抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端的距离BD为10米,请求出立柱AH的长.(结果精确到0.1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
20.为了测量山坡上的信号塔PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端Q的仰角为30°.沿水平地面向前走100米到达B处,测得信号塔顶端P的仰角是60°,求信号塔PQ的高度.
21.【2021·恩施州】乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶D处观测乙居民楼楼底B处的俯角是30°,观测乙居民楼楼顶C处的仰角为15°,已知甲居民楼的高为10 m,求乙居民楼的高(参考数据:≈1.414,≈1.732,结果精确到0.1 m).
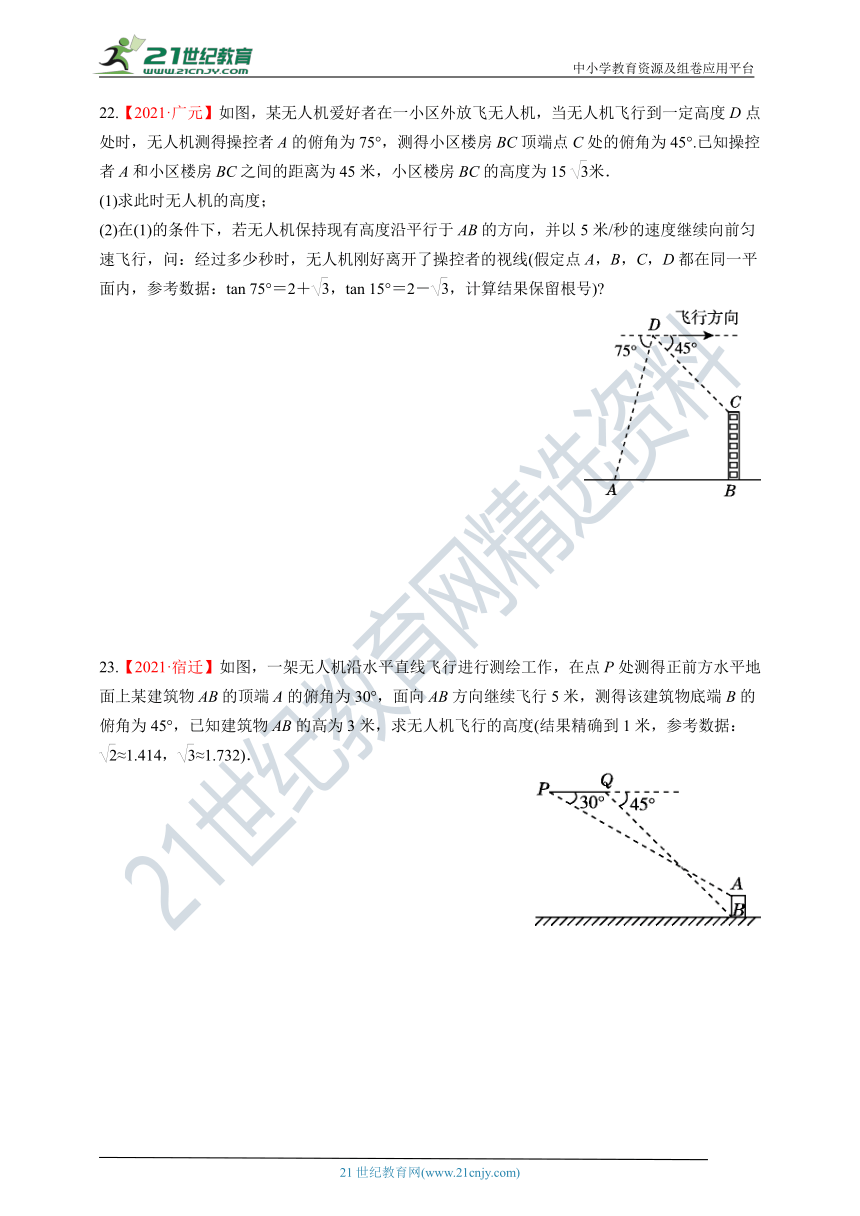
22.【2021·广元】如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,小区楼房BC的高度为15米.
(1)求此时无人机的高度;
(2)在(1)的条件下,若无人机保持现有高度沿平行于AB的方向,并以5米/秒的速度继续向前匀速飞行,问:经过多少秒时,无人机刚好离开了操控者的视线(假定点A,B,C,D都在同一平面内,参考数据:tan 75°=2+,tan 15°=2-,计算结果保留根号)
23.【2021·宿迁】如图,一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:≈1.414,≈1.732).
24.【2021·河北】如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3 km/min的速度在离地面5 km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿45°仰角爬升,到4 km高的A处便立刻转为水平飞行,再过1 min到达B处开始沿直线BC降落,要求
1 min后到达C(10,3)处.
(1)求OA的h关于s的函数解析式,并直接写出2号机的爬升速度;
(2)求BC的h关于s的函数解析式,并预计2号机着陆点的坐标;
(3)通过计算说明两机距离PQ不超过3 km的时长是多少.
[注:(1)及(2)中不必写s的取值范围]
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2020·长沙】从一艘船上测得海岸上高为42 m的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( A )
A.42 m B.14 m C.21 m D.42 m
2.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β.已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( C )
A.asinα+asinβ B.acosα+acosβ C.atanα+atanβ D.
第2题图 第3题图 第4题图
3.如图,为安全起见,游乐园拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是( C )
A.2 m B.2 m C.3 m D.3 m
4.如图,在热气球C处测得地面A,B两点的俯角分别为30°,45°,热气球C的高度CD为100米,点A,D,B在同一直线上,则A,B两点之间的距离是( D )
A.200米 B.200米 C.220米 D.100(+1)米
5.如图,一艘潜水艇在海面下300 m的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960 m到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( A )
A.(480+300) m B.(960+300) m C.780 m D.1 260 m
第5题图 第6题图 第7题图
6.【2021·长春】如图是净月潭国家森林公园一段索道的示意图.已知A,B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( A )
A.30sinα米 B.米 C.30cosα米 D.米
7.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=a;(3)量得测角仪到旗杆的水平距离DB=b,利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.a+btan α B.a+bsin α C.a+ D.a+
【答案】A
【解析】 如图,过点C作CF⊥AB于点F,则四边形CDBF是矩形,∠ACF=α,∴BF=CD=a,CF=BD=b.在Rt△ACF中,AF=CF×tanα=btanα,∴AB=BF+AF=a+btanα.
8.如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,出于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为(参考数据:≈1.4,≈1.7)( )
A.7米 B.14米 C.20米 D.40米
【答案】B
【解析】 如图,过点B作BH⊥AC于点H.∵∠BCH=45°,∠BHC=90°,∴∠HBC=∠BCH=45°,∴HC=HB.设HC=HB=x 米,∵∠A=60°,∴AH=x 米.∵AC=20米,∴x+x=20,∴x=10(3-),∴AH=×10(3-)=10(-1)(米),∴AB=2AH=20(-1)≈14(米).
第8题图 第9题图 第10题图
9.【2020·温州】如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( A )
A.(1.5+150tan α)米 B.米 C.(1.5+150sin α)米 D.米
10.【中考·长春】如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )
A.800sin α米 B.800tan α米 C.米 D.米
【点拨】由题意可知∠CAB=90°,∠B=α,AC=800米,
∴tan α=,
∴AB==米.
【答案】D
11.【2021·重庆A卷】如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度i=1:1.25.若,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为( C )(参考数据:≈1.41,≈1.73)
A.9.0m B.12.8m C.13.1m D.22.7m
【解析】解:∵,DF的坡度i=1:1.25,
∴,解得,
∴,
∴,
∵,,
∴,
∴顶端M与顶端N的高度差为,
【答案】C
第11题图 第12题图
12.【2021·重庆B卷】如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为( )
(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
【解答】解:∵斜坡CD的坡度(或坡比)为i=1:2.4,
∴DE:CE=5:12,
∵DE=50米,
∴CE=120米,
∵BC=150米,
∴BE=150-120=30米,
∴AB=tan50°×30+50
=85.7米.
【答案】D
二、填空题
13.如图,甲、乙是两个高度相等且底面直径之比为1∶2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是 6 cm.
第13题图 第14题图 第15题图
14.【2021·天门】如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为3 m/s,从A处沿水平方向飞行至B处需10 s.同时在地面C处分别测得A处的仰角为75°,B处的仰角为30°,则这架无人机的飞行高度大约是________m(≈1.732,结果保留整数).
【答案】20
【点拨】过点A作AH⊥BC于H,过点B作BD垂直于过点C的水平线,垂足为D,如图.
根据题意得∠ACD=75°,∠BCD=30°,
AB=3×10=30(m),
∵AB∥CD,∴∠ABH=∠BCD=30°.
在Rt△ABH中,AH=AB=15 m,
∵tan∠ABH=,∴BH===15(m).
∵∠ACH=∠ACD-∠BCD=75°-30°=45°,
∴CH=AH=15 m,∴BC=BH+CH=(15+15)m.
在Rt△BCD中,∵∠BCD=30°,
∴BD=BC=≈20(m).
15.【2021·赤峰】某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头C处的高度CD为238米,点A,D,B在同一直线上,则雪道AB的长度约为________米(结果保留整数,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
【答案】438
【点拨】
由题意得∠CAD=50°,∠CBD=45°.
在Rt△CBD中,∠CBD=45°,
∴BD=CD=238米.
在Rt△CAD中,tan∠CAD=,∴AD=≈200米.
∴AB=AD+BD≈200+238=438(米).
16.【2021·广西北部湾经济区】如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为___________米(结果保留根号).
【点拨】
由题意可得,∠ADB=60°,∠ACB=45°,AB=30米.
在Rt△ABC中,∵∠ACB=45°,
∴BC=AB=30米.
在Rt△ABD中,∵∠ADB=60°,
∴BD=AB=10米.
∴CD=BC-BD=(30-10)米.
【答案】30-10
第16题图 第17题图 第18题图
17.【2021·黄冈】如图,建筑物BC上有一高为8 m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为________m(结果保留小数点后一位;参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33).
【点拨】在Rt△BCD中,∠BDC=45°,则BC=CD.
设BC=CD=x m,则AC=(x+8)m.
在Rt△ACD中,tan∠ADC==,
则x+8=x·tan53°,
解得x≈24.2.
故建筑物BC的高约为24.2 m.
【答案】24.2
18.如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200 米到达湖边点N处,测得塔尖点A在湖中的倒影点A'的俯角∠A'NB为45°,则电视塔AB的高度为 米.(结果保留根号)
【答案】100
【解析】 连接AN,易证△ABN≌△A'BN,∴A'N=AN,∠ANB=∠A'NB=45°.∵∠AMB=22.5°,
∴∠MAN=22.5°,∴AN=MN=200 米,∴AB=AN·sin∠ANB=200×sin 45°=200×=100(米).
三、解答题
19.高淳固城湖大桥采用H型塔形斜拉桥结构(如图1),图2是从图1抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端的距离BD为10米,请求出立柱AH的长.(结果精确到0.1米,参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
解:设AH的长为x米,则CH的长为(x-2)米.
在Rt△ABH中,AH=BH·tan 45°,∴BH=x,
∴DH=BH-BD=x-10.
在Rt△CDH中,CH=DH·tan 65°,
∴x-2≈2.14(x-10),解得x≈17.0.
答:立柱AH的长约为17.0米.
20.为了测量山坡上的信号塔PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端Q的仰角为30°.沿水平地面向前走100米到达B处,测得信号塔顶端P的仰角是60°,求信号塔PQ的高度.
解:延长PQ交直线AB于点M,连接AQ,
∴∠PMA=90°.
设PM的长为x米,在Rt△PAM中,∠PAM=45°,
∴AM=PM=x米,∴BM=(x-100)米.
在Rt△PBM中,∵tan ∠PBM=,
∴tan 60°=).
在Rt△QAM中,∵tan ∠QAM=+1)米,
∴PQ=PM-QM=100米.
答:信号塔PQ的高度为100米.
21.【2021·恩施州】乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶D处观测乙居民楼楼底B处的俯角是30°,观测乙居民楼楼顶C处的仰角为15°,已知甲居民楼的高为10 m,求乙居民楼的高(参考数据:≈1.414,≈1.732,结果精确到0.1 m).
解: 如图,作DE⊥BC于点E,CF⊥BD于点F.
在Rt△BED中,BE=AD=10 m,∠EDB=30°,
∴∠EBD=60°,BD=2BE=20 m.
在Rt△CBF中,∠CBF=60°,∴BF=BC,CF=BC.
在Rt△CDF中,∠CDF=45°,∴DF=CF=BC.
∵BD=BF+DF,∴BC+BC=20. ∴BC=≈14.6(m).
答 :乙居民楼的高约为14.6 m.
22.【2021·广元】如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,小区楼房BC的高度为15米.
(1)求此时无人机的高度;
解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,如图所示.
则四边形BCFE是矩形.
由题意得AB=45米,∠DAE=75°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,tan∠DAE=,
∴AE==.
∵四边形BCFE是矩形,∴EF=BC=15米,FC=BE.
在Rt△DCF中,∠DFC=90°,∴∠CDF=∠DCF=45°.
∴CF=DF=DE-15.
∴AB=AE+BE=+DE-15=45.
∴DE=15(2+)米.
答:此时无人机的高度为15(2+)米.
(2)在(1)的条件下,若无人机保持现有高度沿平行于AB的方向,并以5米/秒的速度继续向前匀速飞行,问:经过多少秒时,无人机刚好离开了操控者的视线(假定点A,B,C,D都在同一平面内,参考数据:tan 75°=2+,tan 15°=2-,计算结果保留根号)
解:∵DE=15(2+)米,
∴AE===15(米).
如图,连接AC,过D点作DG∥AB,交AC的延长线于G,作GH⊥AB于H.
在Rt△ABC中,∠ABC=90°,AB=45米,BC=15米,
∴tan ∠BAC===.
在Rt△AGH中,GH=DE=15(2+)米,
∴AH===15(3+2)(米),
∴DG=EH=AH-AE=15(3+2)-15=30+30(米),
(30+30)÷5=6+6(秒).
答:经过6+6秒时,无人机刚好离开了操控者的视线.
23.【2021·宿迁】如图,一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:≈1.414,≈1.732).
解:过点A作AC⊥PQ,交PQ的延长线于点C,如图所示.
设AC=x米.
由题意得PQ=5米,∠APC=30°,∠BQC=45°.
在Rt△APC中,tan ∠APC==tan 30°=,
∴PC=AC=x米.
在Rt△BCQ中,∠BQC=45°,
∴QC=BC=AC+AB=(x+3)米.
∵PC-QC=PQ,∴x-(x+3)=5,解得x=4(+1).
∴BC=4(+1)+3≈14(米).
答:无人机飞行的高度约为14米.
24.【2021·河北】如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3 km/min的速度在离地面5 km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿45°仰角爬升,到4 km高的A处便立刻转为水平飞行,再过1 min到达B处开始沿直线BC降落,要求
1 min后到达C(10,3)处.
(1)求OA的h关于s的函数解析式,并直接写出2号机的爬升速度;
【思路点拨】由爬升角度为45°,可知OA上的点的横、纵坐标相同,由此得到点A的坐标,用待定系数法可求OA的解析式;利用2号机一直保持在1号机的正下方,可知它们飞行的时间和飞行的水平距离相同,由此可求爬升速度.
解:∵2号机爬升角度为45°,
∴OA上的点的横、纵坐标相同.∴A(4,4).
设OA的解析式为h=ks,∴4k=4.
∴k=1.
∴OA的解析式为h=s.
2号机的爬升速度为3km/min.
(2)求BC的h关于s的函数解析式,并预计2号机着陆点的坐标;
【思路点拨】设BC的解析式为h=ms+n,将点B,C的坐标分别代入即可求得;令h=0,求得s,即可得到结果.
解:设BC的解析式为h=ms+n,由题意得B(7,4),
∴解得
∴BC的解析式为h=-s+.
令h=0,则s=19.
∴预计2号机着陆点的坐标为(19,0).
(3)通过计算说明两机距离PQ不超过3 km的时长是多少.
[注:(1)及(2)中不必写s的取值范围]
【思路点拨】由PQ不超过3 km,可得5-h≤3,利用(1)(2)中的解析式得出关于s的不等式组,确定s的取值范围,可得两机距离PQ不超过3 km的飞行的水平距离,再除以1号机的飞行速度,即可得结果.
解:∵PQ不超过3 km,∴5-h≤3.
∴
解得2≤s≤13.
∴两机距离PQ不超过3 km的时长为(13-2)÷3=(min).
28.2.2 应用举例
第1课时 仰角、俯角
一、选择题
1.【2020·长沙】从一艘船上测得海岸上高为42 m的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )
A.42 m B.14 m C.21 m D.42 m
2.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β.已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ C.atanα+atanβ D.
第2题图 第3题图 第4题图
3.如图,为安全起见,游乐园拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 m B.2 m C.3 m D.3 m
4.如图,在热气球C处测得地面A,B两点的俯角分别为30°,45°,热气球C的高度CD为100米,点A,D,B在同一直线上,则A,B两点之间的距离是( )
A.200米 B.200米 C.220米 D.100(+1)米
5.如图,一艘潜水艇在海面下300 m的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960 m到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( )
A.(480+300) m B.(960+300) m C.780 m D.1 260 m
第5题图 第6题图 第7题图
6.【2021·长春】如图是净月潭国家森林公园一段索道的示意图.已知A,B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米 B.米 C.30cosα米 D.米
7.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=a;(3)量得测角仪到旗杆的水平距离DB=b,利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.a+btan α B.a+bsin α C.a+ D.a+
8.如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,出于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为(参考数据:≈1.4,≈1.7)( )
A.7米 B.14米 C.20米 D.40米
第8题图 第9题图 第10题图
9.【2020·温州】如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tan α)米 B.米 C.(1.5+150sin α)米 D.米
10.【中考·长春】如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )
A.800sin α米 B.800tan α米 C.米 D.米
11.【2021·重庆A卷】如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度i=1:1.25.若,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为( )(参考数据:≈1.41,≈1.73)
A.9.0m B.12.8m C.13.1m D.22.7m
第11题图 第12题图
12.【2021·重庆B卷】如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为( )
(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
二、填空题
13.如图,甲、乙是两个高度相等且底面直径之比为1∶2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是 cm.
第13题图 第14题图 第15题图
14.【2021·天门】如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为3 m/s,从A处沿水平方向飞行至B处需10 s.同时在地面C处分别测得A处的仰角为75°,B处的仰角为30°,则这架无人机的飞行高度大约是________m(≈1.732,结果保留整数).
15.【2021·赤峰】某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头C处的高度CD为238米,点A,D,B在同一直线上,则雪道AB的长度约为________米(结果保留整数,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
16.【2021·广西北部湾经济区】如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为___________米(结果保留根号).
第16题图 第17题图 第18题图
17.【2021·黄冈】如图,建筑物BC上有一高为8 m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为________m(结果保留小数点后一位;参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33).
18.如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200 米到达湖边点N处,测得塔尖点A在湖中的倒影点A'的俯角∠A'NB为45°,则电视塔AB的高度为 米.(结果保留根号)
三、解答题
19.高淳固城湖大桥采用H型塔形斜拉桥结构(如图1),图2是从图1抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端的距离BD为10米,请求出立柱AH的长.(结果精确到0.1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
20.为了测量山坡上的信号塔PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端Q的仰角为30°.沿水平地面向前走100米到达B处,测得信号塔顶端P的仰角是60°,求信号塔PQ的高度.
21.【2021·恩施州】乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶D处观测乙居民楼楼底B处的俯角是30°,观测乙居民楼楼顶C处的仰角为15°,已知甲居民楼的高为10 m,求乙居民楼的高(参考数据:≈1.414,≈1.732,结果精确到0.1 m).
22.【2021·广元】如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,小区楼房BC的高度为15米.
(1)求此时无人机的高度;
(2)在(1)的条件下,若无人机保持现有高度沿平行于AB的方向,并以5米/秒的速度继续向前匀速飞行,问:经过多少秒时,无人机刚好离开了操控者的视线(假定点A,B,C,D都在同一平面内,参考数据:tan 75°=2+,tan 15°=2-,计算结果保留根号)
23.【2021·宿迁】如图,一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:≈1.414,≈1.732).
24.【2021·河北】如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3 km/min的速度在离地面5 km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿45°仰角爬升,到4 km高的A处便立刻转为水平飞行,再过1 min到达B处开始沿直线BC降落,要求
1 min后到达C(10,3)处.
(1)求OA的h关于s的函数解析式,并直接写出2号机的爬升速度;
(2)求BC的h关于s的函数解析式,并预计2号机着陆点的坐标;
(3)通过计算说明两机距离PQ不超过3 km的时长是多少.
[注:(1)及(2)中不必写s的取值范围]
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2020·长沙】从一艘船上测得海岸上高为42 m的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( A )
A.42 m B.14 m C.21 m D.42 m
2.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β.已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( C )
A.asinα+asinβ B.acosα+acosβ C.atanα+atanβ D.
第2题图 第3题图 第4题图
3.如图,为安全起见,游乐园拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是( C )
A.2 m B.2 m C.3 m D.3 m
4.如图,在热气球C处测得地面A,B两点的俯角分别为30°,45°,热气球C的高度CD为100米,点A,D,B在同一直线上,则A,B两点之间的距离是( D )
A.200米 B.200米 C.220米 D.100(+1)米
5.如图,一艘潜水艇在海面下300 m的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960 m到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( A )
A.(480+300) m B.(960+300) m C.780 m D.1 260 m
第5题图 第6题图 第7题图
6.【2021·长春】如图是净月潭国家森林公园一段索道的示意图.已知A,B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( A )
A.30sinα米 B.米 C.30cosα米 D.米
7.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=a;(3)量得测角仪到旗杆的水平距离DB=b,利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.a+btan α B.a+bsin α C.a+ D.a+
【答案】A
【解析】 如图,过点C作CF⊥AB于点F,则四边形CDBF是矩形,∠ACF=α,∴BF=CD=a,CF=BD=b.在Rt△ACF中,AF=CF×tanα=btanα,∴AB=BF+AF=a+btanα.
8.如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,出于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为(参考数据:≈1.4,≈1.7)( )
A.7米 B.14米 C.20米 D.40米
【答案】B
【解析】 如图,过点B作BH⊥AC于点H.∵∠BCH=45°,∠BHC=90°,∴∠HBC=∠BCH=45°,∴HC=HB.设HC=HB=x 米,∵∠A=60°,∴AH=x 米.∵AC=20米,∴x+x=20,∴x=10(3-),∴AH=×10(3-)=10(-1)(米),∴AB=2AH=20(-1)≈14(米).
第8题图 第9题图 第10题图
9.【2020·温州】如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( A )
A.(1.5+150tan α)米 B.米 C.(1.5+150sin α)米 D.米
10.【中考·长春】如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )
A.800sin α米 B.800tan α米 C.米 D.米
【点拨】由题意可知∠CAB=90°,∠B=α,AC=800米,
∴tan α=,
∴AB==米.
【答案】D
11.【2021·重庆A卷】如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度i=1:1.25.若,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为( C )(参考数据:≈1.41,≈1.73)
A.9.0m B.12.8m C.13.1m D.22.7m
【解析】解:∵,DF的坡度i=1:1.25,
∴,解得,
∴,
∴,
∵,,
∴,
∴顶端M与顶端N的高度差为,
【答案】C
第11题图 第12题图
12.【2021·重庆B卷】如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为( )
(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
【解答】解:∵斜坡CD的坡度(或坡比)为i=1:2.4,
∴DE:CE=5:12,
∵DE=50米,
∴CE=120米,
∵BC=150米,
∴BE=150-120=30米,
∴AB=tan50°×30+50
=85.7米.
【答案】D
二、填空题
13.如图,甲、乙是两个高度相等且底面直径之比为1∶2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是 6 cm.
第13题图 第14题图 第15题图
14.【2021·天门】如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为3 m/s,从A处沿水平方向飞行至B处需10 s.同时在地面C处分别测得A处的仰角为75°,B处的仰角为30°,则这架无人机的飞行高度大约是________m(≈1.732,结果保留整数).
【答案】20
【点拨】过点A作AH⊥BC于H,过点B作BD垂直于过点C的水平线,垂足为D,如图.
根据题意得∠ACD=75°,∠BCD=30°,
AB=3×10=30(m),
∵AB∥CD,∴∠ABH=∠BCD=30°.
在Rt△ABH中,AH=AB=15 m,
∵tan∠ABH=,∴BH===15(m).
∵∠ACH=∠ACD-∠BCD=75°-30°=45°,
∴CH=AH=15 m,∴BC=BH+CH=(15+15)m.
在Rt△BCD中,∵∠BCD=30°,
∴BD=BC=≈20(m).
15.【2021·赤峰】某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头C处的高度CD为238米,点A,D,B在同一直线上,则雪道AB的长度约为________米(结果保留整数,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
【答案】438
【点拨】
由题意得∠CAD=50°,∠CBD=45°.
在Rt△CBD中,∠CBD=45°,
∴BD=CD=238米.
在Rt△CAD中,tan∠CAD=,∴AD=≈200米.
∴AB=AD+BD≈200+238=438(米).
16.【2021·广西北部湾经济区】如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为___________米(结果保留根号).
【点拨】
由题意可得,∠ADB=60°,∠ACB=45°,AB=30米.
在Rt△ABC中,∵∠ACB=45°,
∴BC=AB=30米.
在Rt△ABD中,∵∠ADB=60°,
∴BD=AB=10米.
∴CD=BC-BD=(30-10)米.
【答案】30-10
第16题图 第17题图 第18题图
17.【2021·黄冈】如图,建筑物BC上有一高为8 m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为________m(结果保留小数点后一位;参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33).
【点拨】在Rt△BCD中,∠BDC=45°,则BC=CD.
设BC=CD=x m,则AC=(x+8)m.
在Rt△ACD中,tan∠ADC==,
则x+8=x·tan53°,
解得x≈24.2.
故建筑物BC的高约为24.2 m.
【答案】24.2
18.如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200 米到达湖边点N处,测得塔尖点A在湖中的倒影点A'的俯角∠A'NB为45°,则电视塔AB的高度为 米.(结果保留根号)
【答案】100
【解析】 连接AN,易证△ABN≌△A'BN,∴A'N=AN,∠ANB=∠A'NB=45°.∵∠AMB=22.5°,
∴∠MAN=22.5°,∴AN=MN=200 米,∴AB=AN·sin∠ANB=200×sin 45°=200×=100(米).
三、解答题
19.高淳固城湖大桥采用H型塔形斜拉桥结构(如图1),图2是从图1抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端的距离BD为10米,请求出立柱AH的长.(结果精确到0.1米,参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
解:设AH的长为x米,则CH的长为(x-2)米.
在Rt△ABH中,AH=BH·tan 45°,∴BH=x,
∴DH=BH-BD=x-10.
在Rt△CDH中,CH=DH·tan 65°,
∴x-2≈2.14(x-10),解得x≈17.0.
答:立柱AH的长约为17.0米.
20.为了测量山坡上的信号塔PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端Q的仰角为30°.沿水平地面向前走100米到达B处,测得信号塔顶端P的仰角是60°,求信号塔PQ的高度.
解:延长PQ交直线AB于点M,连接AQ,
∴∠PMA=90°.
设PM的长为x米,在Rt△PAM中,∠PAM=45°,
∴AM=PM=x米,∴BM=(x-100)米.
在Rt△PBM中,∵tan ∠PBM=,
∴tan 60°=).
在Rt△QAM中,∵tan ∠QAM=+1)米,
∴PQ=PM-QM=100米.
答:信号塔PQ的高度为100米.
21.【2021·恩施州】乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶D处观测乙居民楼楼底B处的俯角是30°,观测乙居民楼楼顶C处的仰角为15°,已知甲居民楼的高为10 m,求乙居民楼的高(参考数据:≈1.414,≈1.732,结果精确到0.1 m).
解: 如图,作DE⊥BC于点E,CF⊥BD于点F.
在Rt△BED中,BE=AD=10 m,∠EDB=30°,
∴∠EBD=60°,BD=2BE=20 m.
在Rt△CBF中,∠CBF=60°,∴BF=BC,CF=BC.
在Rt△CDF中,∠CDF=45°,∴DF=CF=BC.
∵BD=BF+DF,∴BC+BC=20. ∴BC=≈14.6(m).
答 :乙居民楼的高约为14.6 m.
22.【2021·广元】如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,小区楼房BC的高度为15米.
(1)求此时无人机的高度;
解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,如图所示.
则四边形BCFE是矩形.
由题意得AB=45米,∠DAE=75°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,tan∠DAE=,
∴AE==.
∵四边形BCFE是矩形,∴EF=BC=15米,FC=BE.
在Rt△DCF中,∠DFC=90°,∴∠CDF=∠DCF=45°.
∴CF=DF=DE-15.
∴AB=AE+BE=+DE-15=45.
∴DE=15(2+)米.
答:此时无人机的高度为15(2+)米.
(2)在(1)的条件下,若无人机保持现有高度沿平行于AB的方向,并以5米/秒的速度继续向前匀速飞行,问:经过多少秒时,无人机刚好离开了操控者的视线(假定点A,B,C,D都在同一平面内,参考数据:tan 75°=2+,tan 15°=2-,计算结果保留根号)
解:∵DE=15(2+)米,
∴AE===15(米).
如图,连接AC,过D点作DG∥AB,交AC的延长线于G,作GH⊥AB于H.
在Rt△ABC中,∠ABC=90°,AB=45米,BC=15米,
∴tan ∠BAC===.
在Rt△AGH中,GH=DE=15(2+)米,
∴AH===15(3+2)(米),
∴DG=EH=AH-AE=15(3+2)-15=30+30(米),
(30+30)÷5=6+6(秒).
答:经过6+6秒时,无人机刚好离开了操控者的视线.
23.【2021·宿迁】如图,一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:≈1.414,≈1.732).
解:过点A作AC⊥PQ,交PQ的延长线于点C,如图所示.
设AC=x米.
由题意得PQ=5米,∠APC=30°,∠BQC=45°.
在Rt△APC中,tan ∠APC==tan 30°=,
∴PC=AC=x米.
在Rt△BCQ中,∠BQC=45°,
∴QC=BC=AC+AB=(x+3)米.
∵PC-QC=PQ,∴x-(x+3)=5,解得x=4(+1).
∴BC=4(+1)+3≈14(米).
答:无人机飞行的高度约为14米.
24.【2021·河北】如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3 km/min的速度在离地面5 km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿45°仰角爬升,到4 km高的A处便立刻转为水平飞行,再过1 min到达B处开始沿直线BC降落,要求
1 min后到达C(10,3)处.
(1)求OA的h关于s的函数解析式,并直接写出2号机的爬升速度;
【思路点拨】由爬升角度为45°,可知OA上的点的横、纵坐标相同,由此得到点A的坐标,用待定系数法可求OA的解析式;利用2号机一直保持在1号机的正下方,可知它们飞行的时间和飞行的水平距离相同,由此可求爬升速度.
解:∵2号机爬升角度为45°,
∴OA上的点的横、纵坐标相同.∴A(4,4).
设OA的解析式为h=ks,∴4k=4.
∴k=1.
∴OA的解析式为h=s.
2号机的爬升速度为3km/min.
(2)求BC的h关于s的函数解析式,并预计2号机着陆点的坐标;
【思路点拨】设BC的解析式为h=ms+n,将点B,C的坐标分别代入即可求得;令h=0,求得s,即可得到结果.
解:设BC的解析式为h=ms+n,由题意得B(7,4),
∴解得
∴BC的解析式为h=-s+.
令h=0,则s=19.
∴预计2号机着陆点的坐标为(19,0).
(3)通过计算说明两机距离PQ不超过3 km的时长是多少.
[注:(1)及(2)中不必写s的取值范围]
【思路点拨】由PQ不超过3 km,可得5-h≤3,利用(1)(2)中的解析式得出关于s的不等式组,确定s的取值范围,可得两机距离PQ不超过3 km的飞行的水平距离,再除以1号机的飞行速度,即可得结果.
解:∵PQ不超过3 km,∴5-h≤3.
∴
解得2≤s≤13.
∴两机距离PQ不超过3 km的时长为(13-2)÷3=(min).
