28.2.2.2 方位角、坡度、坡角同步练习(含答案)
文档属性
| 名称 | 28.2.2.2 方位角、坡度、坡角同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 16:20:01 | ||
图片预览




文档简介
28.2 解直角三角形及其应用
28.2.2 应用举例
第2课时 方位角、坡度、坡角
一、选择题
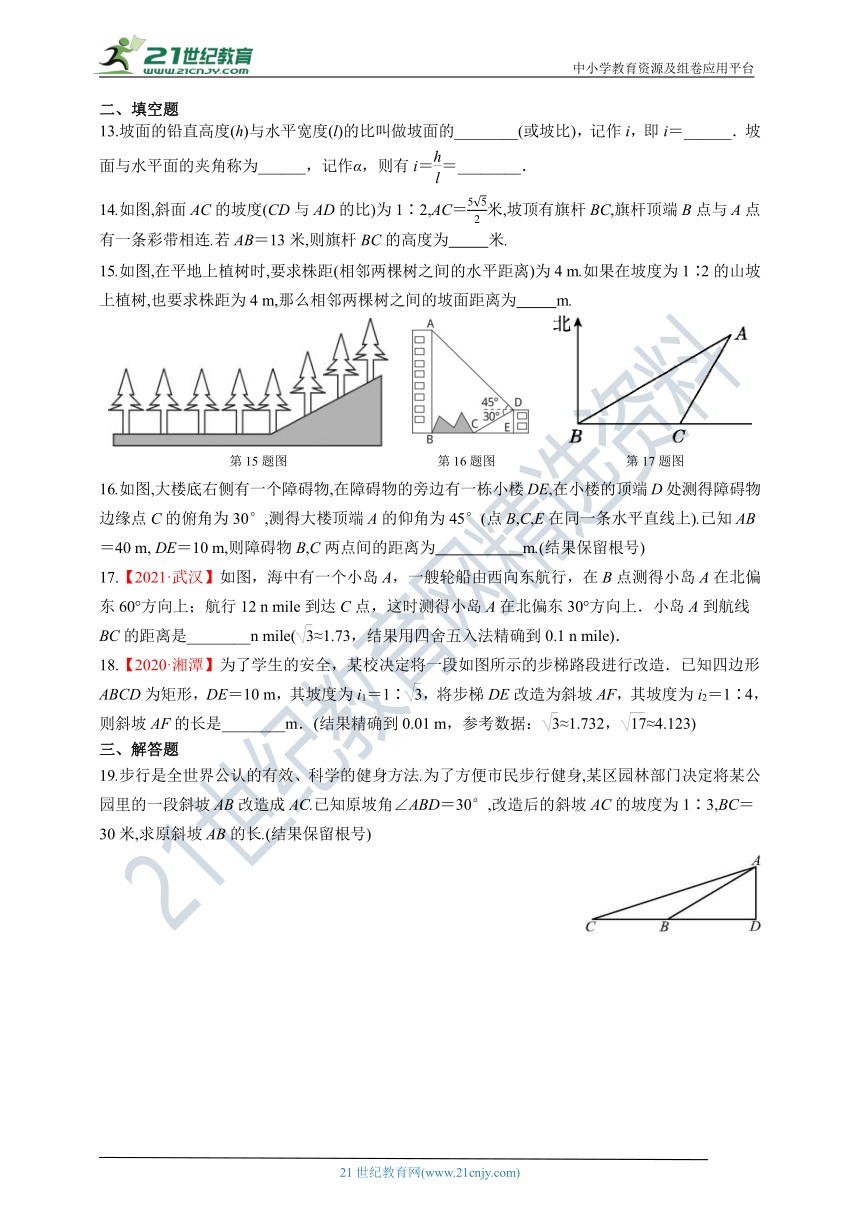
1.如图,以学校(点C)为观测点,小明家(点B)和小丰家(点A)分别位于学校的正南方向和西南方向,并测得AC=6 km,BC=6(1+)km,则小丰家位于小明家的( )
第1题图 第2题图 第3题图
A.南偏西30°方向 B.北偏西30°方向 C.北偏东45°方向 D.南偏东60°方向
2.如图,一艘轮船以40海里/小时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么再过多长时间轮船离灯塔最近 ( )
A.1小时 B.小时 C.2小时 D.2小时
3.如图,有一斜坡AB,坡顶B离地面的高度BC为30 m,斜坡AB的坡度i=1∶2.5,则此斜坡的水平距离AC为( )
A.75 m B.50 m C.30 m D.12 m
4.如图,在坡度为1∶2的山坡上种树,要求相邻两棵树之间的水平距离AC为6米,则斜坡上相邻两树之间的坡面距离AB为( )
A.3米 B.3米 C.6米 D.6米
第4题图 第5题图 第6题图
5.如图为东西流向且河岸平行的一段河道,A,B分别为两岸上一点,且点B在点A正北方向,由点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为( )
A.atan 55°米 B.米 C.米 D.米
6.【2021·金华】如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4cosα米 B.4sinα米 C.4tanα米 D.米
7.【2021·德州】某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5m,调整后的楼梯会加长( ) (sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6米 B.3米 C.2米 D.1米
8.在数学活动课上,九(1)班数学兴趣小组的学生要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离.现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东α方向,测得点P与亭子A之间的距离为200米,则亭子A与亭子B之间的距离为( )
A.(100+100·sin α)米 B.(100+100·tan α)米 C.米 D.米
第8题图 第9题图 第10题图
9.【2021·衡阳】如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
A.7.5米 B.8米 C.9米 D.10米
10.【2021·泰安】如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A,B,C,D,E在同一平面内,斜坡AD的坡度i=1 ∶2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )
A.136.6米 B.86.7米 C.186.7米 D.86.6米
11.【2020·深圳】如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan 70° m B. m C.200sin 70° m D. m
第11题图 第12题图 第14题图
12.【中考·泰安】如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )
A.(30+30)km B.(30+10)km C.(10+30)km D.30 km
二、填空题
13.坡面的铅直高度(h)与水平宽度(l)的比叫做坡面的________(或坡比),记作i,即i=______.坡面与水平面的夹角称为______,记作α,则有i==________.
14.如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=13米,则旗杆BC的高度为 米.
15.如图,在平地上植树时,要求株距(相邻两棵树之间的水平距离)为4 m.如果在坡度为1∶2的山坡上植树,也要求株距为4 m,那么相邻两棵树之间的坡面距离为 m.
第15题图 第16题图 第17题图
16.如图,大楼底右侧有一个障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一条水平直线上).已知AB=40 m, DE=10 m,则障碍物B,C两点间的距离为 m.(结果保留根号)
17.【2021·武汉】如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是________n mile(≈1.73,结果用四舍五入法精确到0.1 n mile).
18.【2020·湘潭】为了学生的安全,某校决定将一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10 m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,则斜坡AF的长是________m.(结果精确到0.01 m,参考数据:≈1.732,≈4.123)
三、解答题
19.步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身,某区园林部门决定将某公园里的一段斜坡AB改造成AC.已知原坡角∠ABD=30°,改造后的斜坡AC的坡度为1∶3,BC=30米,求原斜坡AB的长.(结果保留根号)
20.【巴中中考】如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数.
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响 请说明理由.(参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60,≈1.73)
21.如图,河流的两岸PQ,MN互相平行,河岸MN上有一排间隔为50米的电线杆C,D,E,….某人在河岸PQ的点A处测得∠CAQ=30°,然后沿河岸走了110米到达点B处,测得∠DBQ=45°.求河流的宽度.(结果保留小数点后一位,参考数据:≈1.73)
22.某区域平面示意图如图所示,点D在河的右侧,人民路AB与桥BC垂直.某校数学小组进行研学活动时,在点C处测得点D位于西北方向,又在点A处测得点D位于南偏东65°方向,另测得BC=628 m,AB=400 m,求点D到AB的距离.(结果保留整数,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
23.【2021·资阳】资阳市为实现5G网络全覆盖,2020~2025年拟建设5G基站七千个.如图,在坡度i=1∶2.4的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A,B,C,D均在同一平面内)(参考数据:sin53°≈,cos53°≈,tan53°≈)
(1)求D处的竖直高度;
(2)求基站塔AB的高.
24.【中考·株洲】如图为某区域部分交通线路图,其中直线l1∥l2∥l3,直线l与直线l1,l2,l3都垂直,垂足分别为点A、点B和点C,l2上的点M位于点A的北偏东30°方向上,且BM=km,l3上的点N位于点M的北偏东α方向上,且cosα=,MN=2km,点A和点N是城际铁路线L上的两个相邻的站点.
(1)求l2和l3之间的距离;
(2)若城际火车平均速度为150 km/h,求市民小强乘坐城际火车从站点A到站点N需要多少小时.(结果用分数表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,以学校(点C)为观测点,小明家(点B)和小丰家(点A)分别位于学校的正南方向和西南方向,并测得AC=6 km,BC=6(1+)km,则小丰家位于小明家的( B )
第1题图 第2题图 第3题图
A.南偏西30°方向 B.北偏西30°方向 C.北偏东45°方向 D.南偏东60°方向
2.如图,一艘轮船以40海里/小时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么再过多长时间轮船离灯塔最近 ( A )
A.1小时 B.小时 C.2小时 D.2小时
3.如图,有一斜坡AB,坡顶B离地面的高度BC为30 m,斜坡AB的坡度i=1∶2.5,则此斜坡的水平距离AC为( A )
A.75 m B.50 m C.30 m D.12 m
4.如图,在坡度为1∶2的山坡上种树,要求相邻两棵树之间的水平距离AC为6米,则斜坡上相邻两树之间的坡面距离AB为( B )
A.3米 B.3米 C.6米 D.6米
第4题图 第5题图 第6题图
5.如图为东西流向且河岸平行的一段河道,A,B分别为两岸上一点,且点B在点A正北方向,由点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为( D )
A.atan 55°米 B.米 C.米 D.米
6.【2021·金华】如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( A )
A.4cosα米 B.4sinα米 C.4tanα米 D.米
7.【2021·德州】某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5m,调整后的楼梯会加长( D ) (sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6米 B.3米 C.2米 D.1米
8.在数学活动课上,九(1)班数学兴趣小组的学生要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离.现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东α方向,测得点P与亭子A之间的距离为200米,则亭子A与亭子B之间的距离为( B )
A.(100+100·sin α)米 B.(100+100·tan α)米 C.米 D.米
第8题图 第9题图 第10题图
9.【2021·衡阳】如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( D )
A.7.5米 B.8米 C.9米 D.10米
【解答】解:在Rt△ABC中,∠ACB=90°,BC=6米,
∵sin∠BAC==sin37°≈0.6=,
∴AB≈BC=×6=10(米),
10.【2021·泰安】如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A,B,C,D,E在同一平面内,斜坡AD的坡度i=1 ∶2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )
A.136.6米 B.86.7米 C.186.7米 D.86.6米
【点拨】如图,作DH⊥AB于点H,延长DE交BC于点F.
在Rt△ADH中,AD=130米,DH∶AH=1∶2.4,
∴DH=50米.
由题易知四边形DHBF是矩形,∴BF=DH=50米.
在Rt△EFB中,∠BEF=45°,∴EF=BF=50米.
在Rt△EFC中,CF=EF·tan 60°,∴CF=50×≈86.6(米).
∴BC=BF+CF≈136.6米.
【答案】A
11.【2020·深圳】如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( B )
A.200tan 70° m B. m C.200sin 70° m D. m
第11题图 第12题图 第14题图
12.【中考·泰安】如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( B )
A.(30+30)km B.(30+10)km C.(10+30)km D.30 km
【点拨】根据题意,得∠CAB=65°-20°=45°,∠ACB=40°+20°=60°,AB=30 km.
如图,过点B作BE⊥AC于点E,
∴∠AEB=∠CEB=90°.
在Rt△ABE中,
∵∠EAB=45°,AB=30 km,
∴AE=BE=AB·sin 45°=30×=30(km).
在Rt△CBE中,∵∠ACB=60°,
∴CE===10(km).
∴AC=AE+CE=(30+10)km.
二、填空题
13.坡面的铅直高度(h)与水平宽度(l)的比叫做坡面的________(或坡比),记作i,即i=______.坡面与水平面的夹角称为______,记作α,则有i==________.
【答案】坡度 坡角 tan α
14.如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=13米,则旗杆BC的高度为 9.5 米.
15.如图,在平地上植树时,要求株距(相邻两棵树之间的水平距离)为4 m.如果在坡度为1∶2的山坡上植树,也要求株距为4 m,那么相邻两棵树之间的坡面距离为 2 m.
第15题图 第16题图 第17题图
16.如图,大楼底右侧有一个障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一条水平直线上).已知AB=40 m, DE=10 m,则障碍物B,C两点间的距离为 (30-10) m.(结果保留根号)
17.【2021·武汉】如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是________n mile(≈1.73,结果用四舍五入法精确到0.1 n mile).
【答案】10.4
18.【2020·湘潭】为了学生的安全,某校决定将一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10 m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,则斜坡AF的长是________m.(结果精确到0.01 m,参考数据:≈1.732,≈4.123)
【答案】20.62
三、解答题
19.步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身,某区园林部门决定将某公园里的一段斜坡AB改造成AC.已知原坡角∠ABD=30°,改造后的斜坡AC的坡度为1∶3,BC=30米,求原斜坡AB的长.(结果保留根号)
解:设AD=x.在Rt△ABD中,∠ABD=30°,∴AB=2AD=2x,∴BD=x.
∵斜坡AC的坡度为1∶3,∴CD=3AD=3x.
由题意,得3x-,
∴AB=2x=(30+10)米.
答:原斜坡AB的长为(30+10)米.
20.【巴中中考】如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数.
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响 请说明理由.(参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60,≈1.73)
解:(1)∵∠MAC=60°,∴∠BAC=30°.
又∵BP⊥AC,∴∠APB=90°,∴∠ABP=60°.
又∵∠CBN=29°,∠ABN=90°,
∴∠ABC=119°,∴∠PBC=∠ABC-∠ABP=59°.
(2)不会受到影响.
理由:由(1)可知,∠PBC=59°,∴∠C=90°-∠PBC=31°.
又∵tan 31°≈0.60,∴.
设BP为x海里,则AP=x海里,
∴x=200,解得x≈59.
∵59>50,∴沿海城市B不会受到台风影响.
21.如图,河流的两岸PQ,MN互相平行,河岸MN上有一排间隔为50米的电线杆C,D,E,….某人在河岸PQ的点A处测得∠CAQ=30°,然后沿河岸走了110米到达点B处,测得∠DBQ=45°.求河流的宽度.(结果保留小数点后一位,参考数据:≈1.73)
解:过点D作DH∥CA交PQ于点H,过点D作DG⊥PQ,垂足为G.
∵PQ∥MN,DH∥CA,∴四边形CAHD是平行四边形,
∴AH=CD=50,∠DHQ=∠CAQ=30°.
在Rt△DBG中,∵∠DBG=∠BDG=45°,∴BG=DG,
设BG=DG=x,∴HG=HB+BG=60+x.
在Rt△DHG中,DG=HG·tan 30°,即x=(60+x),
解得x≈81.7.
答:河流的宽度约为81.7米.
22.某区域平面示意图如图所示,点D在河的右侧,人民路AB与桥BC垂直.某校数学小组进行研学活动时,在点C处测得点D位于西北方向,又在点A处测得点D位于南偏东65°方向,另测得BC=628 m,AB=400 m,求点D到AB的距离.(结果保留整数,参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
解:过点D作DE⊥AB于点E,过点D作DF⊥BC于点F,则四边形BFDE是矩形.
设DE=x.
在Rt△ADE中,∠AED=90°,tan ∠DAE=,
∴AE=,
∴BE=AB-AE=400-.
∵BF=DE=x,∴CF=BC-BF=628-x.
在Rt△CDF中,∠DFC=90°,∠DCF=45°,
∴∠CDF=45°,∴∠CDF=∠DCF,∴DF=CF=628-x.
∵BE=DF,即400-=628-x,解得x=428.
答:点D到AB的距离约为428 m.
23.【2021·资阳】资阳市为实现5G网络全覆盖,2020~2025年拟建设5G基站七千个.如图,在坡度i=1∶2.4的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A,B,C,D均在同一平面内)(参考数据:sin53°≈,cos53°≈,tan53°≈)
(1)求D处的竖直高度;
解:如图,过点D作地面的垂线,垂足为点M.
∵斜坡CB的坡度i=1∶2.4,
∴==.
设DM=5k米,则CM=12k米.
在Rt△CDM中,CD=13米,由勾股定理得
CM2+DM2=CD2,
即(5k)2+(12k)2=132,
解得k=1(负值舍去).
∴DM=5米,CM=12米.
答:D处的竖直高度为5米.
(2)求基站塔AB的高.
解:如图,延长AB交地面于点F,过点D作DE⊥AF,
垂足为点E.由斜坡CB的坡度i=1∶2.4,
可设DE=12a米,则BE=5a米,
又∵∠ACF=45°,
∴AF=CF=(12+12a)米.
∴AE=AF-EF=12+12a-5=(7+12a)米.
在Rt△ADE中,∠ADE=53°,DE=12a米,
AE=(7+12a)米,
∵tan∠ADE=,∴≈,解得a≈.
∴AE=7+12a≈28米,BE=5a≈米.
∴AB=AE-BE≈28-=(米).
答:基站塔AB的高约为米.
24.【中考·株洲】如图为某区域部分交通线路图,其中直线l1∥l2∥l3,直线l与直线l1,l2,l3都垂直,垂足分别为点A、点B和点C,l2上的点M位于点A的北偏东30°方向上,且BM=km,l3上的点N位于点M的北偏东α方向上,且cosα=,MN=2km,点A和点N是城际铁路线L上的两个相邻的站点.
(1)求l2和l3之间的距离;
解:过点M作MD⊥NC于点D,
∵cos α=,MN=2km,
∴cos α===,
解得DM=2 km.
∴l2和l3之间的距离为2 km.
(2)若城际火车平均速度为150 km/h,求市民小强乘坐城际火车从站点A到站点N需要多少小时.(结果用分数表示)
解:∵点M位于点A的北偏东30°方向上,且BM=km,
∴tan 30°===,
∴AB=3 km,∴AC=3+2=5 (km).
∵MN=2km,DM=2 km,
∴DN==4(km).
易知CD=BM,
∴NC=DN+BM=5km,
∴AN===10 (km).
∵城际火车平均速度为150 km/h,
∴市民小强乘坐城际火车从站点A到站点N需要10÷150=(h).
28.2.2 应用举例
第2课时 方位角、坡度、坡角
一、选择题
1.如图,以学校(点C)为观测点,小明家(点B)和小丰家(点A)分别位于学校的正南方向和西南方向,并测得AC=6 km,BC=6(1+)km,则小丰家位于小明家的( )
第1题图 第2题图 第3题图
A.南偏西30°方向 B.北偏西30°方向 C.北偏东45°方向 D.南偏东60°方向
2.如图,一艘轮船以40海里/小时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么再过多长时间轮船离灯塔最近 ( )
A.1小时 B.小时 C.2小时 D.2小时
3.如图,有一斜坡AB,坡顶B离地面的高度BC为30 m,斜坡AB的坡度i=1∶2.5,则此斜坡的水平距离AC为( )
A.75 m B.50 m C.30 m D.12 m
4.如图,在坡度为1∶2的山坡上种树,要求相邻两棵树之间的水平距离AC为6米,则斜坡上相邻两树之间的坡面距离AB为( )
A.3米 B.3米 C.6米 D.6米
第4题图 第5题图 第6题图
5.如图为东西流向且河岸平行的一段河道,A,B分别为两岸上一点,且点B在点A正北方向,由点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为( )
A.atan 55°米 B.米 C.米 D.米
6.【2021·金华】如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4cosα米 B.4sinα米 C.4tanα米 D.米
7.【2021·德州】某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5m,调整后的楼梯会加长( ) (sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6米 B.3米 C.2米 D.1米
8.在数学活动课上,九(1)班数学兴趣小组的学生要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离.现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东α方向,测得点P与亭子A之间的距离为200米,则亭子A与亭子B之间的距离为( )
A.(100+100·sin α)米 B.(100+100·tan α)米 C.米 D.米
第8题图 第9题图 第10题图
9.【2021·衡阳】如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
A.7.5米 B.8米 C.9米 D.10米
10.【2021·泰安】如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A,B,C,D,E在同一平面内,斜坡AD的坡度i=1 ∶2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )
A.136.6米 B.86.7米 C.186.7米 D.86.6米
11.【2020·深圳】如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan 70° m B. m C.200sin 70° m D. m
第11题图 第12题图 第14题图
12.【中考·泰安】如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )
A.(30+30)km B.(30+10)km C.(10+30)km D.30 km
二、填空题
13.坡面的铅直高度(h)与水平宽度(l)的比叫做坡面的________(或坡比),记作i,即i=______.坡面与水平面的夹角称为______,记作α,则有i==________.
14.如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=13米,则旗杆BC的高度为 米.
15.如图,在平地上植树时,要求株距(相邻两棵树之间的水平距离)为4 m.如果在坡度为1∶2的山坡上植树,也要求株距为4 m,那么相邻两棵树之间的坡面距离为 m.
第15题图 第16题图 第17题图
16.如图,大楼底右侧有一个障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一条水平直线上).已知AB=40 m, DE=10 m,则障碍物B,C两点间的距离为 m.(结果保留根号)
17.【2021·武汉】如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是________n mile(≈1.73,结果用四舍五入法精确到0.1 n mile).
18.【2020·湘潭】为了学生的安全,某校决定将一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10 m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,则斜坡AF的长是________m.(结果精确到0.01 m,参考数据:≈1.732,≈4.123)
三、解答题
19.步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身,某区园林部门决定将某公园里的一段斜坡AB改造成AC.已知原坡角∠ABD=30°,改造后的斜坡AC的坡度为1∶3,BC=30米,求原斜坡AB的长.(结果保留根号)
20.【巴中中考】如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数.
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响 请说明理由.(参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60,≈1.73)
21.如图,河流的两岸PQ,MN互相平行,河岸MN上有一排间隔为50米的电线杆C,D,E,….某人在河岸PQ的点A处测得∠CAQ=30°,然后沿河岸走了110米到达点B处,测得∠DBQ=45°.求河流的宽度.(结果保留小数点后一位,参考数据:≈1.73)
22.某区域平面示意图如图所示,点D在河的右侧,人民路AB与桥BC垂直.某校数学小组进行研学活动时,在点C处测得点D位于西北方向,又在点A处测得点D位于南偏东65°方向,另测得BC=628 m,AB=400 m,求点D到AB的距离.(结果保留整数,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
23.【2021·资阳】资阳市为实现5G网络全覆盖,2020~2025年拟建设5G基站七千个.如图,在坡度i=1∶2.4的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A,B,C,D均在同一平面内)(参考数据:sin53°≈,cos53°≈,tan53°≈)
(1)求D处的竖直高度;
(2)求基站塔AB的高.
24.【中考·株洲】如图为某区域部分交通线路图,其中直线l1∥l2∥l3,直线l与直线l1,l2,l3都垂直,垂足分别为点A、点B和点C,l2上的点M位于点A的北偏东30°方向上,且BM=km,l3上的点N位于点M的北偏东α方向上,且cosα=,MN=2km,点A和点N是城际铁路线L上的两个相邻的站点.
(1)求l2和l3之间的距离;
(2)若城际火车平均速度为150 km/h,求市民小强乘坐城际火车从站点A到站点N需要多少小时.(结果用分数表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,以学校(点C)为观测点,小明家(点B)和小丰家(点A)分别位于学校的正南方向和西南方向,并测得AC=6 km,BC=6(1+)km,则小丰家位于小明家的( B )
第1题图 第2题图 第3题图
A.南偏西30°方向 B.北偏西30°方向 C.北偏东45°方向 D.南偏东60°方向
2.如图,一艘轮船以40海里/小时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么再过多长时间轮船离灯塔最近 ( A )
A.1小时 B.小时 C.2小时 D.2小时
3.如图,有一斜坡AB,坡顶B离地面的高度BC为30 m,斜坡AB的坡度i=1∶2.5,则此斜坡的水平距离AC为( A )
A.75 m B.50 m C.30 m D.12 m
4.如图,在坡度为1∶2的山坡上种树,要求相邻两棵树之间的水平距离AC为6米,则斜坡上相邻两树之间的坡面距离AB为( B )
A.3米 B.3米 C.6米 D.6米
第4题图 第5题图 第6题图
5.如图为东西流向且河岸平行的一段河道,A,B分别为两岸上一点,且点B在点A正北方向,由点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为( D )
A.atan 55°米 B.米 C.米 D.米
6.【2021·金华】如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( A )
A.4cosα米 B.4sinα米 C.4tanα米 D.米
7.【2021·德州】某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5m,调整后的楼梯会加长( D ) (sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6米 B.3米 C.2米 D.1米
8.在数学活动课上,九(1)班数学兴趣小组的学生要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离.现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东α方向,测得点P与亭子A之间的距离为200米,则亭子A与亭子B之间的距离为( B )
A.(100+100·sin α)米 B.(100+100·tan α)米 C.米 D.米
第8题图 第9题图 第10题图
9.【2021·衡阳】如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( D )
A.7.5米 B.8米 C.9米 D.10米
【解答】解:在Rt△ABC中,∠ACB=90°,BC=6米,
∵sin∠BAC==sin37°≈0.6=,
∴AB≈BC=×6=10(米),
10.【2021·泰安】如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A,B,C,D,E在同一平面内,斜坡AD的坡度i=1 ∶2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )
A.136.6米 B.86.7米 C.186.7米 D.86.6米
【点拨】如图,作DH⊥AB于点H,延长DE交BC于点F.
在Rt△ADH中,AD=130米,DH∶AH=1∶2.4,
∴DH=50米.
由题易知四边形DHBF是矩形,∴BF=DH=50米.
在Rt△EFB中,∠BEF=45°,∴EF=BF=50米.
在Rt△EFC中,CF=EF·tan 60°,∴CF=50×≈86.6(米).
∴BC=BF+CF≈136.6米.
【答案】A
11.【2020·深圳】如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( B )
A.200tan 70° m B. m C.200sin 70° m D. m
第11题图 第12题图 第14题图
12.【中考·泰安】如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( B )
A.(30+30)km B.(30+10)km C.(10+30)km D.30 km
【点拨】根据题意,得∠CAB=65°-20°=45°,∠ACB=40°+20°=60°,AB=30 km.
如图,过点B作BE⊥AC于点E,
∴∠AEB=∠CEB=90°.
在Rt△ABE中,
∵∠EAB=45°,AB=30 km,
∴AE=BE=AB·sin 45°=30×=30(km).
在Rt△CBE中,∵∠ACB=60°,
∴CE===10(km).
∴AC=AE+CE=(30+10)km.
二、填空题
13.坡面的铅直高度(h)与水平宽度(l)的比叫做坡面的________(或坡比),记作i,即i=______.坡面与水平面的夹角称为______,记作α,则有i==________.
【答案】坡度 坡角 tan α
14.如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=13米,则旗杆BC的高度为 9.5 米.
15.如图,在平地上植树时,要求株距(相邻两棵树之间的水平距离)为4 m.如果在坡度为1∶2的山坡上植树,也要求株距为4 m,那么相邻两棵树之间的坡面距离为 2 m.
第15题图 第16题图 第17题图
16.如图,大楼底右侧有一个障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一条水平直线上).已知AB=40 m, DE=10 m,则障碍物B,C两点间的距离为 (30-10) m.(结果保留根号)
17.【2021·武汉】如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是________n mile(≈1.73,结果用四舍五入法精确到0.1 n mile).
【答案】10.4
18.【2020·湘潭】为了学生的安全,某校决定将一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10 m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,则斜坡AF的长是________m.(结果精确到0.01 m,参考数据:≈1.732,≈4.123)
【答案】20.62
三、解答题
19.步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身,某区园林部门决定将某公园里的一段斜坡AB改造成AC.已知原坡角∠ABD=30°,改造后的斜坡AC的坡度为1∶3,BC=30米,求原斜坡AB的长.(结果保留根号)
解:设AD=x.在Rt△ABD中,∠ABD=30°,∴AB=2AD=2x,∴BD=x.
∵斜坡AC的坡度为1∶3,∴CD=3AD=3x.
由题意,得3x-,
∴AB=2x=(30+10)米.
答:原斜坡AB的长为(30+10)米.
20.【巴中中考】如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台风中心距离小岛200海里.
(1)过点B作BP⊥AC于点P,求∠PBC的度数.
(2)据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响 请说明理由.(参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60,≈1.73)
解:(1)∵∠MAC=60°,∴∠BAC=30°.
又∵BP⊥AC,∴∠APB=90°,∴∠ABP=60°.
又∵∠CBN=29°,∠ABN=90°,
∴∠ABC=119°,∴∠PBC=∠ABC-∠ABP=59°.
(2)不会受到影响.
理由:由(1)可知,∠PBC=59°,∴∠C=90°-∠PBC=31°.
又∵tan 31°≈0.60,∴.
设BP为x海里,则AP=x海里,
∴x=200,解得x≈59.
∵59>50,∴沿海城市B不会受到台风影响.
21.如图,河流的两岸PQ,MN互相平行,河岸MN上有一排间隔为50米的电线杆C,D,E,….某人在河岸PQ的点A处测得∠CAQ=30°,然后沿河岸走了110米到达点B处,测得∠DBQ=45°.求河流的宽度.(结果保留小数点后一位,参考数据:≈1.73)
解:过点D作DH∥CA交PQ于点H,过点D作DG⊥PQ,垂足为G.
∵PQ∥MN,DH∥CA,∴四边形CAHD是平行四边形,
∴AH=CD=50,∠DHQ=∠CAQ=30°.
在Rt△DBG中,∵∠DBG=∠BDG=45°,∴BG=DG,
设BG=DG=x,∴HG=HB+BG=60+x.
在Rt△DHG中,DG=HG·tan 30°,即x=(60+x),
解得x≈81.7.
答:河流的宽度约为81.7米.
22.某区域平面示意图如图所示,点D在河的右侧,人民路AB与桥BC垂直.某校数学小组进行研学活动时,在点C处测得点D位于西北方向,又在点A处测得点D位于南偏东65°方向,另测得BC=628 m,AB=400 m,求点D到AB的距离.(结果保留整数,参考数据:sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
解:过点D作DE⊥AB于点E,过点D作DF⊥BC于点F,则四边形BFDE是矩形.
设DE=x.
在Rt△ADE中,∠AED=90°,tan ∠DAE=,
∴AE=,
∴BE=AB-AE=400-.
∵BF=DE=x,∴CF=BC-BF=628-x.
在Rt△CDF中,∠DFC=90°,∠DCF=45°,
∴∠CDF=45°,∴∠CDF=∠DCF,∴DF=CF=628-x.
∵BE=DF,即400-=628-x,解得x=428.
答:点D到AB的距离约为428 m.
23.【2021·资阳】资阳市为实现5G网络全覆盖,2020~2025年拟建设5G基站七千个.如图,在坡度i=1∶2.4的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A,B,C,D均在同一平面内)(参考数据:sin53°≈,cos53°≈,tan53°≈)
(1)求D处的竖直高度;
解:如图,过点D作地面的垂线,垂足为点M.
∵斜坡CB的坡度i=1∶2.4,
∴==.
设DM=5k米,则CM=12k米.
在Rt△CDM中,CD=13米,由勾股定理得
CM2+DM2=CD2,
即(5k)2+(12k)2=132,
解得k=1(负值舍去).
∴DM=5米,CM=12米.
答:D处的竖直高度为5米.
(2)求基站塔AB的高.
解:如图,延长AB交地面于点F,过点D作DE⊥AF,
垂足为点E.由斜坡CB的坡度i=1∶2.4,
可设DE=12a米,则BE=5a米,
又∵∠ACF=45°,
∴AF=CF=(12+12a)米.
∴AE=AF-EF=12+12a-5=(7+12a)米.
在Rt△ADE中,∠ADE=53°,DE=12a米,
AE=(7+12a)米,
∵tan∠ADE=,∴≈,解得a≈.
∴AE=7+12a≈28米,BE=5a≈米.
∴AB=AE-BE≈28-=(米).
答:基站塔AB的高约为米.
24.【中考·株洲】如图为某区域部分交通线路图,其中直线l1∥l2∥l3,直线l与直线l1,l2,l3都垂直,垂足分别为点A、点B和点C,l2上的点M位于点A的北偏东30°方向上,且BM=km,l3上的点N位于点M的北偏东α方向上,且cosα=,MN=2km,点A和点N是城际铁路线L上的两个相邻的站点.
(1)求l2和l3之间的距离;
解:过点M作MD⊥NC于点D,
∵cos α=,MN=2km,
∴cos α===,
解得DM=2 km.
∴l2和l3之间的距离为2 km.
(2)若城际火车平均速度为150 km/h,求市民小强乘坐城际火车从站点A到站点N需要多少小时.(结果用分数表示)
解:∵点M位于点A的北偏东30°方向上,且BM=km,
∴tan 30°===,
∴AB=3 km,∴AC=3+2=5 (km).
∵MN=2km,DM=2 km,
∴DN==4(km).
易知CD=BM,
∴NC=DN+BM=5km,
∴AN===10 (km).
∵城际火车平均速度为150 km/h,
∴市民小强乘坐城际火车从站点A到站点N需要10÷150=(h).
