2022年北师大版七年级数学下册2.2.1 同位角及平行公理 同步练习(Word版含答案)
文档属性
| 名称 | 2022年北师大版七年级数学下册2.2.1 同位角及平行公理 同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 269.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 14:42:54 | ||
图片预览


文档简介
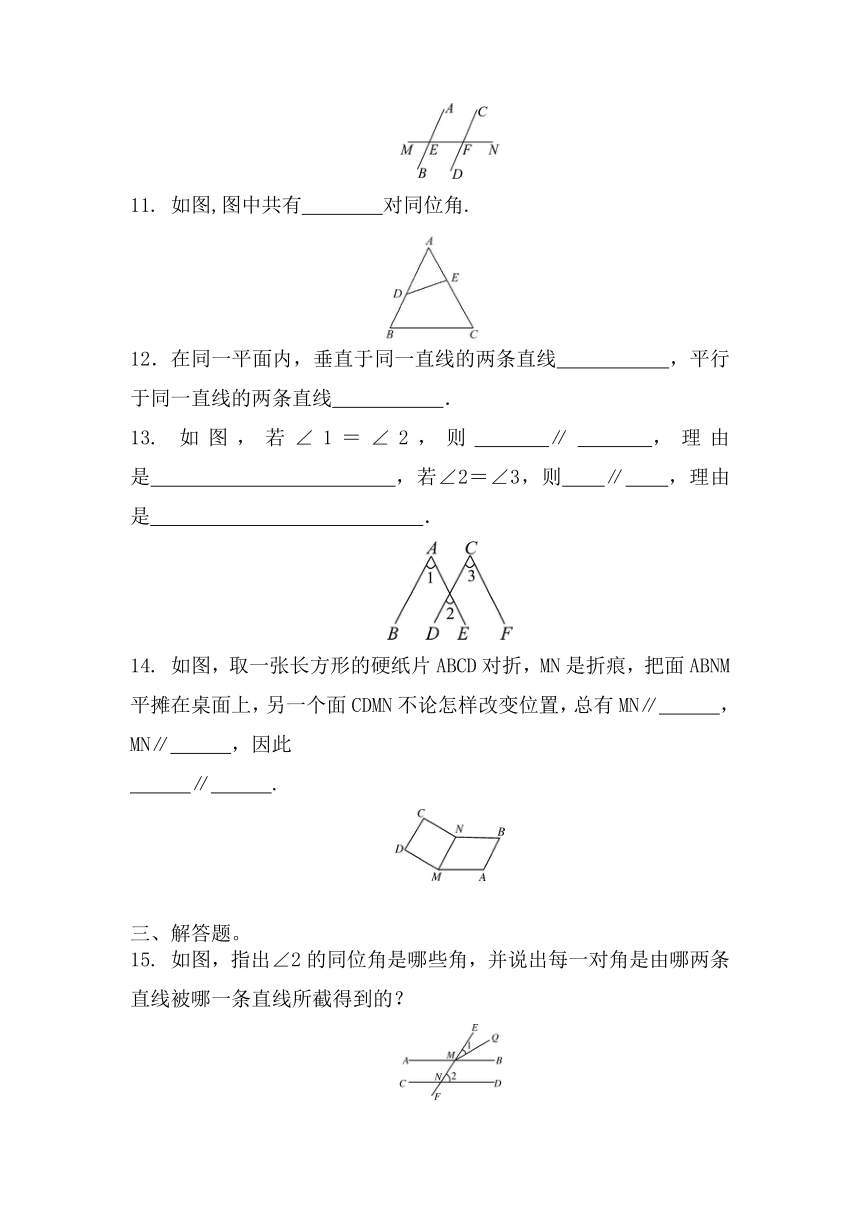
2.2.1 同位角及平行公理
一、单项选择题。
1.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,∠1=100°,要使a∥b,必须具备的另一个条件是( )
A.∠2=100° B.∠3=80° C.∠3=100° D.∠4=80°
3. 如图下列说法不正确的是( )
A.∠1与∠2是同位角 B.∠2与∠3是同位角
C.∠1与∠3是同位角 D.∠1与∠3不是同位角
4.若直线a∥b,b∥c,则a∥c的依据是( )
A.过一点有且只有一条直线和已知直线平行 B.等量代换
C.等式的性质 D.平行于同一条直线的两直线平行
5.如图,下列能判断AB∥CD的是( )
A.∠1=∠2 B.∠1=∠3 C.∠3=∠4 D.∠2=∠4
6.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线垂直
B.过一点有且只有一条直线与已知直线平行
C.在平面内,两条直线的位置关系有相交、垂直和平行三种
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
7.下列图形中,由∠1=∠2能得到AB∥CD的是( )
8. 如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )
A.∠2=35° B.∠2=45° C.∠2=55° D.∠2=125°
二、填空题。
9. 如图所示,若∠1=∠C,则 ∥ ;若∠2=∠C,则 ∥ .
10.如图,直线MN分别交直线AB、CD于E、F,其中∠AEF的对顶角是 ,∠BEF的同位角是 .
11. 如图,图中共有 对同位角.
12.在同一平面内,垂直于同一直线的两条直线 ,平行于同一直线的两条直线 .
13. 如图,若∠1=∠2,则 ∥ ,理由是 ,若∠2=∠3,则 ∥ ,理由是 .
14. 如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,另一个面CDMN不论怎样改变位置,总有MN∥ ,MN∥ ,因此
∥ .
三、解答题。
15. 如图,指出∠2的同位角是哪些角,并说出每一对角是由哪两条直线被哪一条直线所截得到的?
16. 如图所示,直线AB、CD被直线EF所截,若∠1=∠2,那么AB与CD是否平行?为什么?
17. 如图,∠1+∠2=180°,试问:AE与FC会平行吗?说明理由.
18. 如图所示,已知∠A=∠B,点A、C、D在同一直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,则CE∥AB,请说明理由.
19. 如图,∠1=∠2=65°.
(1)∠3等于多少度?
(2)直线AB、CD平行吗?说明你的理由.
20. 如图所示,点B、D是直线MN上的两点,已知∠1=∠2,你能说明AB∥CD成立吗?若不能说明,请添加一个条件,使AB∥CD,并就你添加的条件说明AB∥CD的理由.
答案:
一、
1-8 ACCDC DBC
二、
9. AB CD AC BD
10. ∠BEM ∠DFN
11. 4
12. 互相平行 互相平行
13. AB CD 同位角相等,两直线平行 AE CF 同位角相等,两直线平行
14. CD AB CD AB
三、
15. 解: ∠2的同位角是∠1、∠EMB,分别是由直线MQ、CD被直线EF所截,直线MB、ND被直线EF所截得到的.
16. 解: AB∥CD,理由:∵∠1=∠BMF(对顶角相等),又∵∠1=∠2(已知),∴∠BMF=∠2.∴AB∥CD(同位角相等,两直线平行).
17. 解:平行,理由:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,∴AE∥FC.
18. 解:∵∠A=∠B,∠DCB=∠A+∠B,∴∠A=∠DCB,∵∠DCE=∠DCB,∴∠DCE=∠A,∴CE∥AB.
19. 解:(1)∵∠3=∠2,∠1=∠2=65°,∴∠3=65°;
(2)AB∥CD,∵∠1=∠3,∴AB∥CD(同位角相等,两直线平行).
20. 解:不能,添加条件:∠BDF=∠MBE或∠EBN=∠FDN,∵∠MBE=∠BDF,又∵∠1=∠2,∴∠MBA=∠BDC,∴AB∥CD.
一、单项选择题。
1.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,∠1=100°,要使a∥b,必须具备的另一个条件是( )
A.∠2=100° B.∠3=80° C.∠3=100° D.∠4=80°
3. 如图下列说法不正确的是( )
A.∠1与∠2是同位角 B.∠2与∠3是同位角
C.∠1与∠3是同位角 D.∠1与∠3不是同位角
4.若直线a∥b,b∥c,则a∥c的依据是( )
A.过一点有且只有一条直线和已知直线平行 B.等量代换
C.等式的性质 D.平行于同一条直线的两直线平行
5.如图,下列能判断AB∥CD的是( )
A.∠1=∠2 B.∠1=∠3 C.∠3=∠4 D.∠2=∠4
6.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线垂直
B.过一点有且只有一条直线与已知直线平行
C.在平面内,两条直线的位置关系有相交、垂直和平行三种
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
7.下列图形中,由∠1=∠2能得到AB∥CD的是( )
8. 如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )
A.∠2=35° B.∠2=45° C.∠2=55° D.∠2=125°
二、填空题。
9. 如图所示,若∠1=∠C,则 ∥ ;若∠2=∠C,则 ∥ .
10.如图,直线MN分别交直线AB、CD于E、F,其中∠AEF的对顶角是 ,∠BEF的同位角是 .
11. 如图,图中共有 对同位角.
12.在同一平面内,垂直于同一直线的两条直线 ,平行于同一直线的两条直线 .
13. 如图,若∠1=∠2,则 ∥ ,理由是 ,若∠2=∠3,则 ∥ ,理由是 .
14. 如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,另一个面CDMN不论怎样改变位置,总有MN∥ ,MN∥ ,因此
∥ .
三、解答题。
15. 如图,指出∠2的同位角是哪些角,并说出每一对角是由哪两条直线被哪一条直线所截得到的?
16. 如图所示,直线AB、CD被直线EF所截,若∠1=∠2,那么AB与CD是否平行?为什么?
17. 如图,∠1+∠2=180°,试问:AE与FC会平行吗?说明理由.
18. 如图所示,已知∠A=∠B,点A、C、D在同一直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,则CE∥AB,请说明理由.
19. 如图,∠1=∠2=65°.
(1)∠3等于多少度?
(2)直线AB、CD平行吗?说明你的理由.
20. 如图所示,点B、D是直线MN上的两点,已知∠1=∠2,你能说明AB∥CD成立吗?若不能说明,请添加一个条件,使AB∥CD,并就你添加的条件说明AB∥CD的理由.
答案:
一、
1-8 ACCDC DBC
二、
9. AB CD AC BD
10. ∠BEM ∠DFN
11. 4
12. 互相平行 互相平行
13. AB CD 同位角相等,两直线平行 AE CF 同位角相等,两直线平行
14. CD AB CD AB
三、
15. 解: ∠2的同位角是∠1、∠EMB,分别是由直线MQ、CD被直线EF所截,直线MB、ND被直线EF所截得到的.
16. 解: AB∥CD,理由:∵∠1=∠BMF(对顶角相等),又∵∠1=∠2(已知),∴∠BMF=∠2.∴AB∥CD(同位角相等,两直线平行).
17. 解:平行,理由:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,∴AE∥FC.
18. 解:∵∠A=∠B,∠DCB=∠A+∠B,∴∠A=∠DCB,∵∠DCE=∠DCB,∴∠DCE=∠A,∴CE∥AB.
19. 解:(1)∵∠3=∠2,∠1=∠2=65°,∴∠3=65°;
(2)AB∥CD,∵∠1=∠3,∴AB∥CD(同位角相等,两直线平行).
20. 解:不能,添加条件:∠BDF=∠MBE或∠EBN=∠FDN,∵∠MBE=∠BDF,又∵∠1=∠2,∴∠MBA=∠BDC,∴AB∥CD.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
