2021-2022学年华东师大版九年级数学下册第27章 圆 单元测试训练卷(word版 含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册第27章 圆 单元测试训练卷(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览


文档简介
华东师大版九年级数学下册
第27章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. ⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5 B.6 C.7 D.8
2. ⊙O的圆心O到直线l的距离为d,⊙O的半径为r,且d,r是关于x的方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值是( )
A.1 B.2 C.4 D.-4
3. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
A.100° B.110° C.120° D.130°
4. 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
5. 如图,△ABC内接于圆O,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62° B.31° C.28° D.56°
6. 如图,AB,AC是⊙O的两条弦,∠BAC=25°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
A.25° B.30° C.35° D.40°
7. 如图,将边长为3的正方形铁丝框ABCD(面积记为S1)变形为以点B为圆心,BC为半径的扇形(面积记为S2),则S1与S2的关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
8. 如图,半圆O的直径AB=7,弦AC,BD相交于点E,弦CD=,且BD=5,则DE等于( )
A.2 B.4 C. D.
9.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A. B. C. D.π
10. 如图,P是⊙O外一点,OP交⊙O于点A,OA=AP,甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
甲:以点A为圆心,AP长为半径画弧,交⊙O于点B,则直线BP即为所求.
乙:过点A作直线MN⊥OP,以点O为圆心,OP为半径画弧,交射线AM于点B,连结OB,交⊙O于点C,直线CP即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
A.甲正确,乙错误 B.乙正确,甲错误
C.两人都正确 D.两人都错误
二.填空题(共6小题,4*6=24)
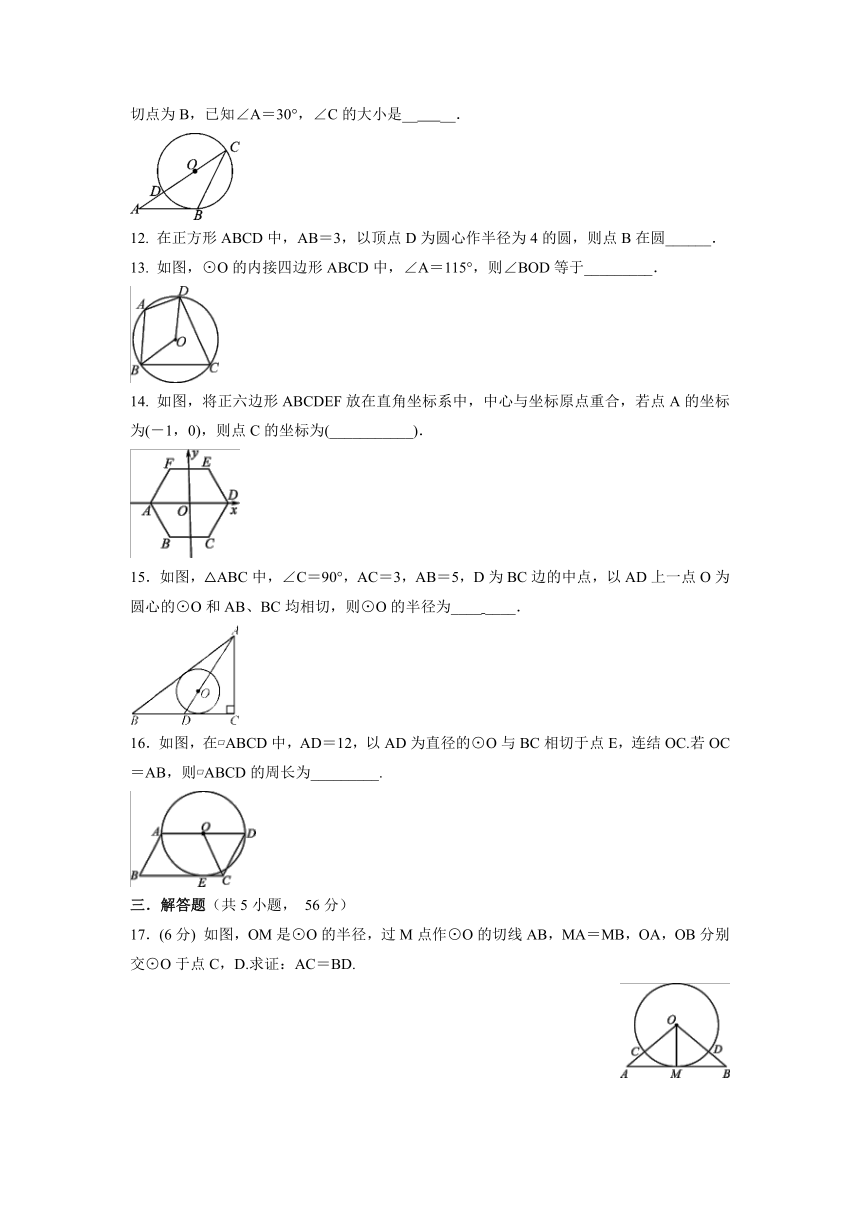
11. 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B,已知∠A=30°,∠C的大小是__ __.
12. 在正方形ABCD中,AB=3,以顶点D为圆心作半径为4的圆,则点B在圆______.
13. 如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于_________.
14. 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-1,0),则点C的坐标为(___________).
15.如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为____ ____.
16.如图,在 ABCD中,AD=12,以AD为直径的⊙O与BC相切于点E,连结OC.若OC=AB,则 ABCD的周长为_________.
三.解答题(共5小题, 56分)
17.(6分) 如图,OM是⊙O的半径,过M点作⊙O的切线AB,MA=MB,OA,OB分别交⊙O于点C,D.求证:AC=BD.
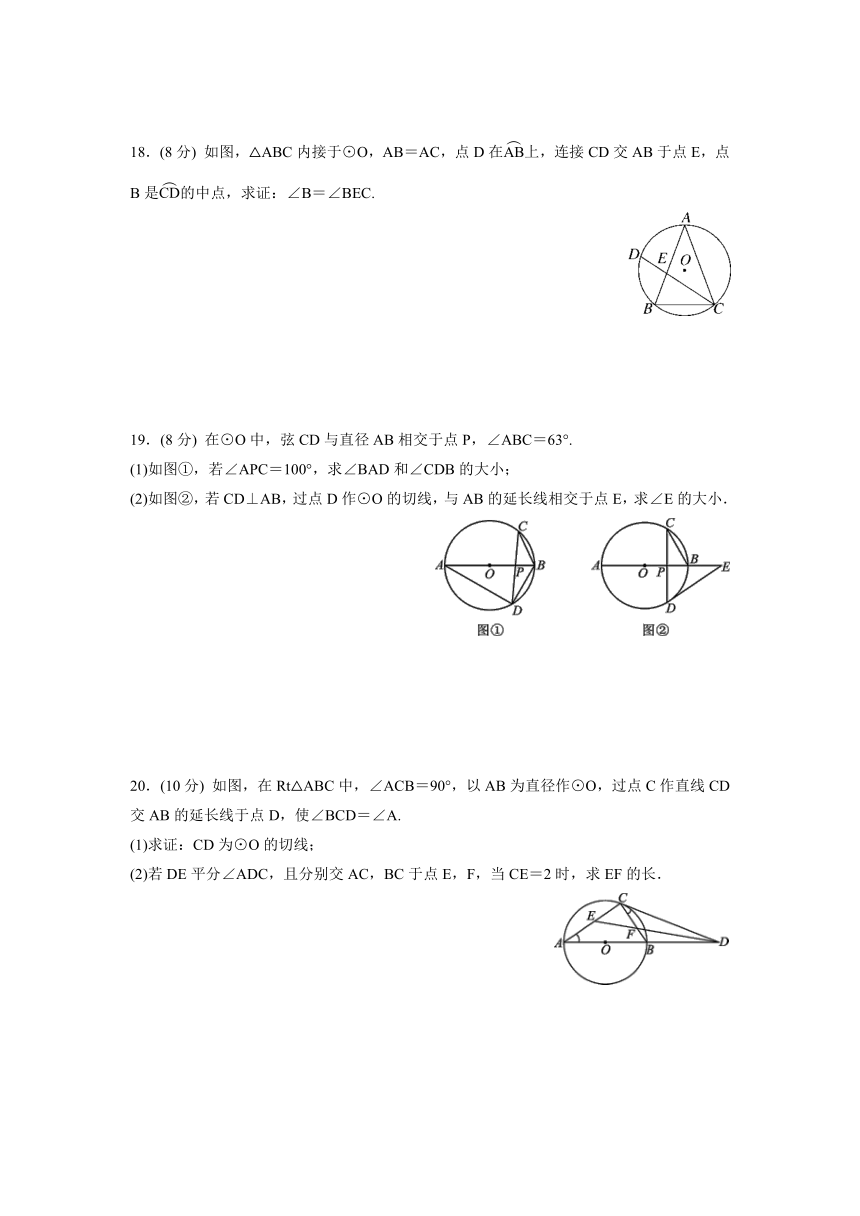
18.(8分) 如图,△ABC内接于⊙O,AB=AC,点D在上,连接CD交AB于点E,点B是的中点,求证:∠B=∠BEC.
19.(8分) 在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(1)如图①,若∠APC=100°,求∠BAD和∠CDB的大小;
(2)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
20.(10分) 如图,在Rt△ABC中,∠ACB=90°,以AB为直径作⊙O,过点C作直线CD交AB的延长线于点D,使∠BCD=∠A.
(1)求证:CD为⊙O的切线;
(2)若DE平分∠ADC,且分别交AC,BC于点E,F,当CE=2时,求EF的长.
21.(12分) 如图,AB与⊙O相切于点C,OA、OB分别交⊙O于点D、E,CD=CE.
(1)求证:OA=OB;
(2)已知AB=4,OA=4,求阴影部分的面积.
22.(12分) 如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)求证:AE为⊙O的切线;
(2)当BC=8,AC=12时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.
参考答案
1-5ACBBB 6-10DBABC
11.30°
12.外
13.130°
14.,-
15.
16.24+6
17.证明:∵AB与⊙O相切,∴OM⊥AB,∵MA=MB,∴OA=OB,∵OC=OD,∴OA-OC=OB-OD,∴AC=BD
18.证明:∵点B是的中点,∴∠BCD=∠BAC,∴∠BCD+∠ACD=∠BAC+∠ACD,即∠ACB=∠BEC.又∵AB=AC,∴∠B=∠ACB,∴∠B=∠BEC.
19.解:(1)∵∠APC是△PBC的一个外角,∴∠C=∠APC-∠ABC=100°-63°=37°,由圆周角定理得:∠BAD=∠C=37°,∠ADC=∠ABC=63°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠CDB=∠ADB-∠ADC=90°-63°=27°
(2)连接OD,如图②所示:∵CD⊥AB,∴∠CPB=90°,∴∠PCB=90°-∠ABC=90°-63°=27°,∵DE是⊙O的切线,∴DE⊥OD,∴∠ODE=90°,∵∠BOD=2∠PCB=54°,∴∠E=90°-∠BOD=90°-54°=36°
20.解:(1)证明:连接OC,∵AB为⊙O的直径,∠ACB=90°,∴点C在⊙O上,∠A+∠ABC=90°,又∵OC=OB,∴∠ABC=∠OCB,∵∠BCD=∠A,∴∠BCD+∠OCB=90°,即∠OCD=90°,∵OC是圆O的半径,∴CD是⊙O的切线
(2)∵DE平分∠ADC,∴∠CDE=∠ADE,又∵∠BCD=∠A,∴∠A+∠ADE=∠BCD+∠CDF,即∠CEF=∠CFE,∵∠ACB=90°,CE=2,∴CE=CF=2,∴EF==2
21.(1)证明:连接OC.∵AB与⊙O相切于点C,∴OC⊥AB.∴∠ACO=∠BCO=90°.∵CD=CE,∴∠AOC=∠BOC.在△AOC和△BOC中, ∴△AOC≌△BOC,∴OA=OB.
(2)解:∵△AOC≌△BOC,∴AC=BC=AB=2.∵OB=OA=4,且△OCB是直角三角形,∴根据勾股定理,得OC==2,∴OC=OB,∴∠B=30°,∴∠BOC=60°.∴S阴影=S△BOC-S扇形OCE=×2×2-=2-π.
22.解:(1)连结OM,∵AC=AB,AE平分∠BAC,∴AE⊥BC,∵OB=OM,∴∠OBM=∠OMB,∵BM平分∠ABC,∴∠OBM=∠CBM,∴∠OMB=∠CBM,∴OM∥DC,又∵AE⊥BC,∴AE⊥OM,∴AE是⊙O的切线
(2)设⊙O的半径为R,∵OM∥BE,∴△OMA∽△BEA,∴=,即=,解得R=3,∴⊙O的半径为3
(3)过点O作OH⊥BG于点H,则BG=2BH,∵∠OME=∠MEH=∠EHO=90°,∴四边形OMEH是矩形,∴HE=OM=3,∴BH=1,∴BG=2BH=2
第27章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. ⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5 B.6 C.7 D.8
2. ⊙O的圆心O到直线l的距离为d,⊙O的半径为r,且d,r是关于x的方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值是( )
A.1 B.2 C.4 D.-4
3. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
A.100° B.110° C.120° D.130°
4. 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
5. 如图,△ABC内接于圆O,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62° B.31° C.28° D.56°
6. 如图,AB,AC是⊙O的两条弦,∠BAC=25°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
A.25° B.30° C.35° D.40°
7. 如图,将边长为3的正方形铁丝框ABCD(面积记为S1)变形为以点B为圆心,BC为半径的扇形(面积记为S2),则S1与S2的关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
8. 如图,半圆O的直径AB=7,弦AC,BD相交于点E,弦CD=,且BD=5,则DE等于( )
A.2 B.4 C. D.
9.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A. B. C. D.π
10. 如图,P是⊙O外一点,OP交⊙O于点A,OA=AP,甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
甲:以点A为圆心,AP长为半径画弧,交⊙O于点B,则直线BP即为所求.
乙:过点A作直线MN⊥OP,以点O为圆心,OP为半径画弧,交射线AM于点B,连结OB,交⊙O于点C,直线CP即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
A.甲正确,乙错误 B.乙正确,甲错误
C.两人都正确 D.两人都错误
二.填空题(共6小题,4*6=24)
11. 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B,已知∠A=30°,∠C的大小是__ __.
12. 在正方形ABCD中,AB=3,以顶点D为圆心作半径为4的圆,则点B在圆______.
13. 如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于_________.
14. 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-1,0),则点C的坐标为(___________).
15.如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为____ ____.
16.如图,在 ABCD中,AD=12,以AD为直径的⊙O与BC相切于点E,连结OC.若OC=AB,则 ABCD的周长为_________.
三.解答题(共5小题, 56分)
17.(6分) 如图,OM是⊙O的半径,过M点作⊙O的切线AB,MA=MB,OA,OB分别交⊙O于点C,D.求证:AC=BD.
18.(8分) 如图,△ABC内接于⊙O,AB=AC,点D在上,连接CD交AB于点E,点B是的中点,求证:∠B=∠BEC.
19.(8分) 在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(1)如图①,若∠APC=100°,求∠BAD和∠CDB的大小;
(2)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
20.(10分) 如图,在Rt△ABC中,∠ACB=90°,以AB为直径作⊙O,过点C作直线CD交AB的延长线于点D,使∠BCD=∠A.
(1)求证:CD为⊙O的切线;
(2)若DE平分∠ADC,且分别交AC,BC于点E,F,当CE=2时,求EF的长.
21.(12分) 如图,AB与⊙O相切于点C,OA、OB分别交⊙O于点D、E,CD=CE.
(1)求证:OA=OB;
(2)已知AB=4,OA=4,求阴影部分的面积.
22.(12分) 如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)求证:AE为⊙O的切线;
(2)当BC=8,AC=12时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.
参考答案
1-5ACBBB 6-10DBABC
11.30°
12.外
13.130°
14.,-
15.
16.24+6
17.证明:∵AB与⊙O相切,∴OM⊥AB,∵MA=MB,∴OA=OB,∵OC=OD,∴OA-OC=OB-OD,∴AC=BD
18.证明:∵点B是的中点,∴∠BCD=∠BAC,∴∠BCD+∠ACD=∠BAC+∠ACD,即∠ACB=∠BEC.又∵AB=AC,∴∠B=∠ACB,∴∠B=∠BEC.
19.解:(1)∵∠APC是△PBC的一个外角,∴∠C=∠APC-∠ABC=100°-63°=37°,由圆周角定理得:∠BAD=∠C=37°,∠ADC=∠ABC=63°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠CDB=∠ADB-∠ADC=90°-63°=27°
(2)连接OD,如图②所示:∵CD⊥AB,∴∠CPB=90°,∴∠PCB=90°-∠ABC=90°-63°=27°,∵DE是⊙O的切线,∴DE⊥OD,∴∠ODE=90°,∵∠BOD=2∠PCB=54°,∴∠E=90°-∠BOD=90°-54°=36°
20.解:(1)证明:连接OC,∵AB为⊙O的直径,∠ACB=90°,∴点C在⊙O上,∠A+∠ABC=90°,又∵OC=OB,∴∠ABC=∠OCB,∵∠BCD=∠A,∴∠BCD+∠OCB=90°,即∠OCD=90°,∵OC是圆O的半径,∴CD是⊙O的切线
(2)∵DE平分∠ADC,∴∠CDE=∠ADE,又∵∠BCD=∠A,∴∠A+∠ADE=∠BCD+∠CDF,即∠CEF=∠CFE,∵∠ACB=90°,CE=2,∴CE=CF=2,∴EF==2
21.(1)证明:连接OC.∵AB与⊙O相切于点C,∴OC⊥AB.∴∠ACO=∠BCO=90°.∵CD=CE,∴∠AOC=∠BOC.在△AOC和△BOC中, ∴△AOC≌△BOC,∴OA=OB.
(2)解:∵△AOC≌△BOC,∴AC=BC=AB=2.∵OB=OA=4,且△OCB是直角三角形,∴根据勾股定理,得OC==2,∴OC=OB,∴∠B=30°,∴∠BOC=60°.∴S阴影=S△BOC-S扇形OCE=×2×2-=2-π.
22.解:(1)连结OM,∵AC=AB,AE平分∠BAC,∴AE⊥BC,∵OB=OM,∴∠OBM=∠OMB,∵BM平分∠ABC,∴∠OBM=∠CBM,∴∠OMB=∠CBM,∴OM∥DC,又∵AE⊥BC,∴AE⊥OM,∴AE是⊙O的切线
(2)设⊙O的半径为R,∵OM∥BE,∴△OMA∽△BEA,∴=,即=,解得R=3,∴⊙O的半径为3
(3)过点O作OH⊥BG于点H,则BG=2BH,∵∠OME=∠MEH=∠EHO=90°,∴四边形OMEH是矩形,∴HE=OM=3,∴BH=1,∴BG=2BH=2
