第五章对函数的再探索测试（附答案）

一、选择题(每小题有且只有一个答案是正确的，请将正确答案的字母代号填写在题后相应的括号内)
1.一个正比例函数的图像过点（2，-3），它的表达式为（ ）
A . B. C. D.
2.把抛物线向左平移1个单位，然后向上平移3个单位，则平移后抛物线的表达式 （ ）
A． B．
C． D．．
3.已知反比例函数，下列结论不正确的是（ ）
A.图象经过点（1，1） B.图象在第一、三象限
C.当时， D.当时，随着的增大而增大
4.目前，全球淡水资源日益减少，提倡全社会节约用水．据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升.小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x分钟后，水龙头滴出y毫升的水，请写出y与x之间的函数关系式是
A．y=0.05x B． y=5x C．y=100x D．y=0.05x+100
5.（2010遵义）在一次 “寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志点A、
B,A、B两点到“宝藏”点的距离都是，则“宝藏”点的坐标是（ C ）
A． Ｂ．　　 Ｃ．或　　Ｄ．或
6．若二次函数y=(m+1)x2-mx+m2-2m-3的图象经过原点，则m的值必为（ ）
A．-1或3 B．-1
C．3 D．-3或1
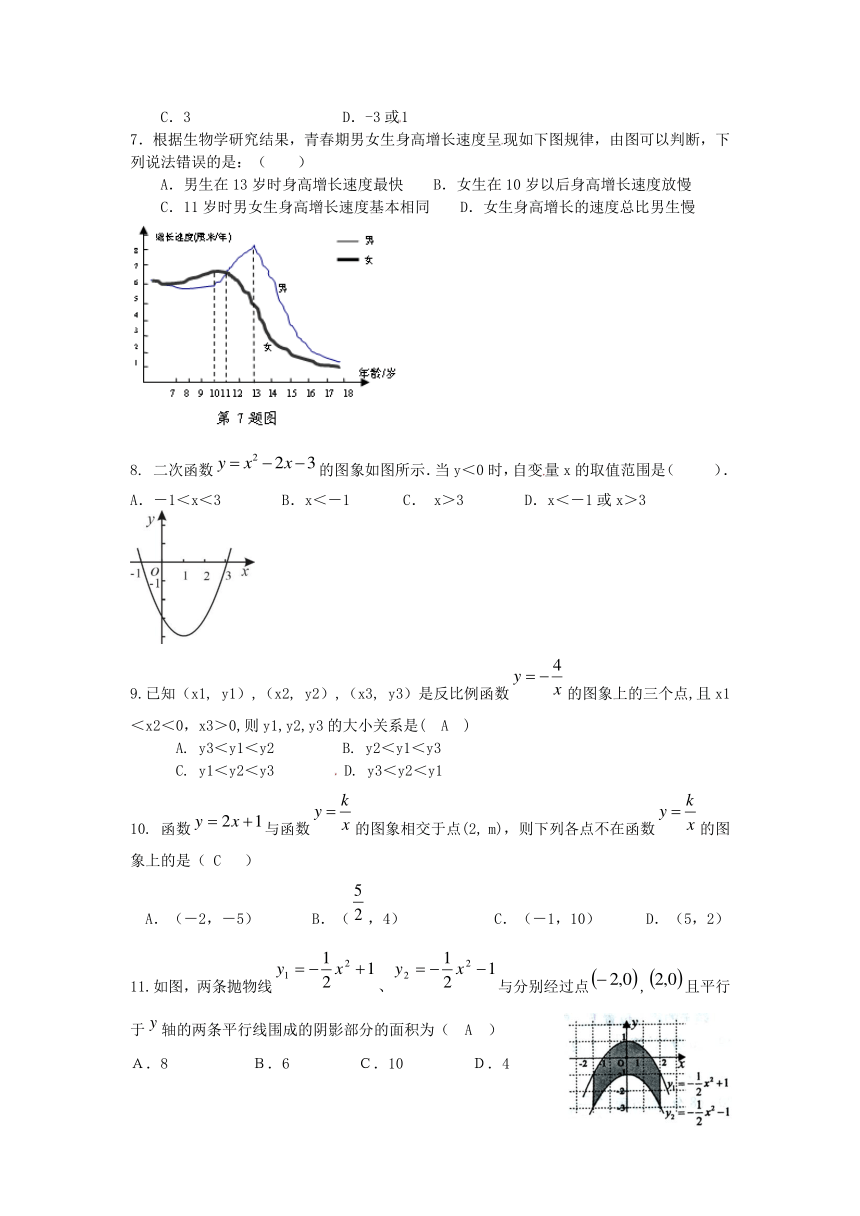
7．根据生物学研究结果，青春期男女生身高增长速度呈现如下图规律，由图可以判断，下列说法错误的是：（ ）
A．男生在13岁时身高增长速度最快 B．女生在10岁以后身高增长速度放慢
C．11岁时男女生身高增长速度基本相同 D．女生身高增长的速度总比男生慢
8. 二次函数的图象如图所示．当y＜0时，自变量x的取值范围是（ ）．
A．－1＜x＜3 B．x＜－1 C． x＞3 D．x＜－1或x＞3
9.已知（x1, y1）,（x2, y2）,（x3, y3）是反比例函数的图象上的三个点,且x1＜x2＜0，x3＞0,则y1,y2,y3的大小关系是( A )
A. y3＜y1＜y2 B. y2＜y1＜y3
C. y1＜y2＜y3 D. y3＜y2＜y1
10. 函数与函数的图象相交于点(2, m)，则下列各点不在函数的图象上的是（ C ）
A．（－2，－5） B．（，4） C．（－1，10） D．（5，2）
11.如图，两条抛物线、与分别经过点,且平行于轴的两条平行线围成的阴影部分的面积为（ A ）
Ａ．8　 Ｂ．6　 Ｃ．10　 Ｄ．4　
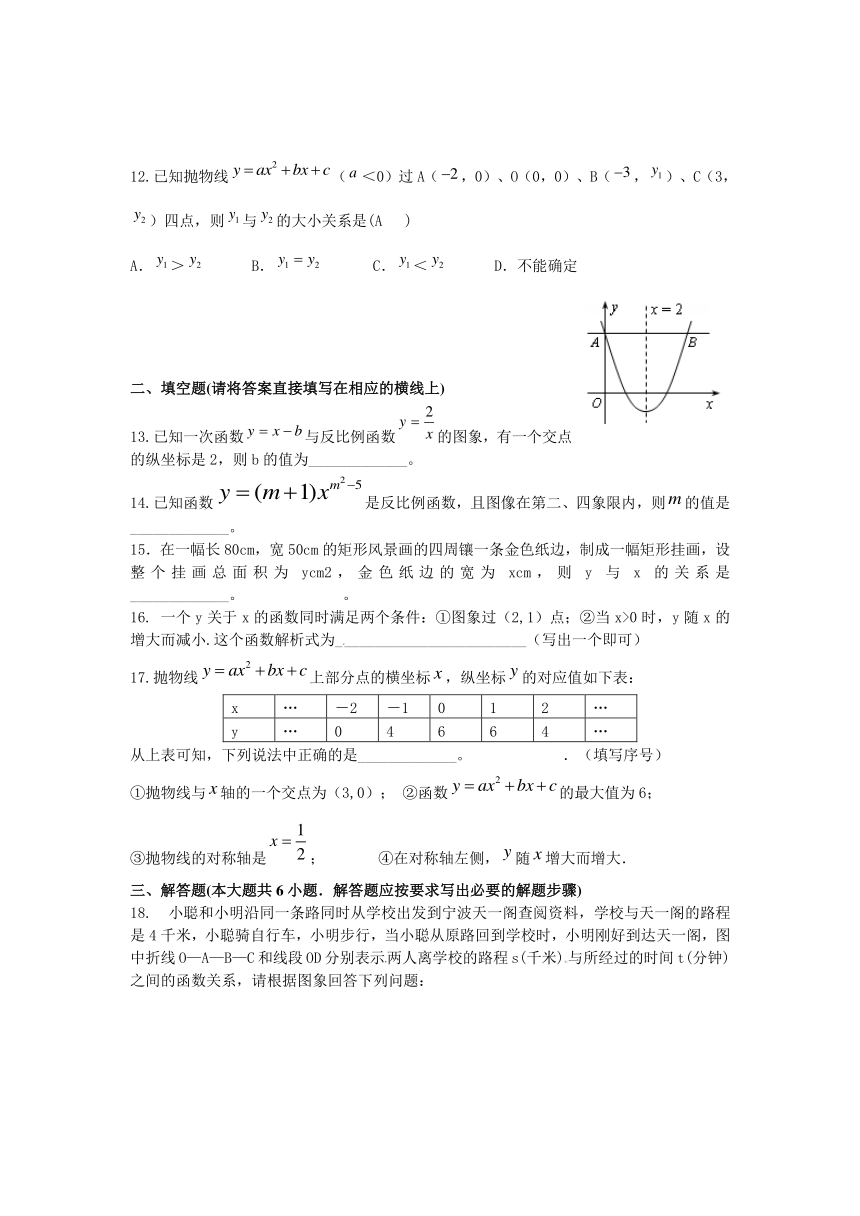
12.已知抛物线（＜0）过A（，0）、O（0，0）、B（，）、C（3，）四点，则与的大小关系是(A )
A．＞ B． C．＜ D．不能确定
二、填空题(请将答案直接填写在相应的横线上)
13.已知一次函数与反比例函数的图象，有一个交点的纵坐标是2，则b的值为_____________。
14.已知函数是反比例函数，且图像在第二、四象限内，则的值是_____________。
15．在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂画，设整个挂画总面积为ycm2，金色纸边的宽为xcm，则y与x的关系是_____________。 。
16. 一个y关于x的函数同时满足两个条件：①图象过（2,1）点；②当x>0时，y随x的增大而减小.这个函数解析式为_________________________（写出一个即可）
17.抛物线上部分点的横坐标，纵坐标的对应值如下表：
x
…
－2
－1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知，下列说法中正确的是_____________。 　　 ．（填写序号）
①抛物线与轴的一个交点为（3,0）； ②函数的最大值为6；
③抛物线的对称轴是；　 　　④在对称轴左侧，随增大而增大．
三、解答题(本大题共6小题．解答题应按要求写出必要的解题步骤)
18. 小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁，图中折线O—A—B—C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系，请根据图象回答下列问题：
(1)小聪在天一阁查阅资料的时间为________分钟，小聪返回学校的速度为________千米/分钟．
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系；
(3)当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
19.已知函数y=mx2－6x＋1（m是常数）．
⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
⑵若该函数的图象与x轴只有一个交点，求m的值．
20．某学校要印制一批《学生手册》，甲印刷厂提出：每本收1元印刷费，另收500元制版费；乙印刷厂提出：每本收2元印刷费，不收制版费．
(1)分别写出甲、乙两厂的收费(元) 、 (元)与印制数量(本)之间的关系式； (4分)
(2)问：该学校选择哪间印刷厂印制《学生手册》比较合算？请说明理由． (4分)
21.如图，已知一次函数与反比例函数的图象交于A、B两点．
（1）求A、B两点的坐标；
（2）观察图象，可知一次函数值小于反比例函数值的的取值范围是 ．（把答案直接写在相应位置上）
22.如图，已知二次函数的图象经过A（2，0）、B（0，－6）
两点。
（1）求这个二次函数的解析式
（2）设该二次函数的对称轴与轴交于点C，连结BA、BC，求△ABC的面积。
23.学校计划用地面砖铺设教学楼前矩形广场的地面已知矩形广场地面的长为100米，宽为80米.图案设计如图所示：广场的四角为小正方形，阴影部分为四个矩形，四个矩形的宽都为小正方形的边长，阴影部分铺绿色地面砖，其余部分铺白色地面砖.
（1）要使铺白色地面砖的面积为5200平方米，那么矩形广场四角的小正方形的边长为多少米？
（2）如果铺白色地面砖的费用为每平方米30元，铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时，铺广场地面的总费用最少？最少费用是多少？
参考答案：
一、选择题1,A 2.B 3.D 4.B 5.C 6.C 7.D 8.A 9.A 10.C 11.A 12.A
二、填空题 13.-1 14.-2 15. y=4x2+260x＋4000. 16.答案不唯一 17. ①③④
三、解答题
19. 【答案】解：⑴当x=0时，．
所以不论为何值，函数的图象经过轴上的一个定点（0，1）．
⑵①当时，函数的图象与轴只有一个交点；
②当时，若函数的图象与轴只有一个交点，则方程有两个相等的实数根，所以，．
综上，若函数的图象与轴只有一个交点，则的值为0或9．
20. 【答案】解：(1)，．
(2)当>时，即>,则<500 ，
当＝时， 即＝,则＝500，·
当<时，即 <, 则>500，
∴该学校印制学生手册数量小于500本时应选择乙厂合算，当印制学生手册数量大于500本时应选择甲厂合算，当印制学生手册数量等于500本时选择两厂费用都一样 ．
21. 解：（1）由题意得：
解之得： 或
∴A、B两点坐标分别为A、B
（2）的取值范围是：或
22.解：（1）把A（2，0）、B（0，－6）代入
得：
解得
∴这个二次函数的解析式为
（2）∵该抛物线对称轴为直线
∴点C的坐标为（4，0）
∴
∴
23. 解：（1）设矩形广场四角的小正方形的边长为米，根据题意，得：
整理，得：
解之，得：
经检验，均适合题意.
所以，要使铺白色地面砖的面积为5200平方米，则矩形广场四角的小正方形的边长为35米或10米.
（2）设铺矩形广场地面的总费用为元，广场四角的小正方形的边长为米，则，
即：
配方得，
当时，的值最小，最小值为199500.
所以，当矩形广场四角的小正方形的边长为22.5米时，所铺广场地面的总费用最少，最少费用为199500元.