28.2.2直线和圆的位置关系(1)
文档属性
| 名称 | 28.2.2直线和圆的位置关系(1) |
|
|
| 格式 | zip | ||
| 文件大小 | 31.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-30 00:00:00 | ||
图片预览

文档简介
周期律 28.2.2直线与圆的位置关系
教学内容
28.2.2直线与圆的位置关系
课型
新授课
主备人
执教人
林立英
教学目标
1.理解直线与圆有相交、相切、相离三种位置关系.
2.了解切线的概念,探索切线与过切点的直径之间的关系.
教学重点
1、经历探索直线与圆位置关系的过程.
2、理解直线与圆的三种位置关系.
3、了解切线的概念以及切线的性质.
一、复习引入
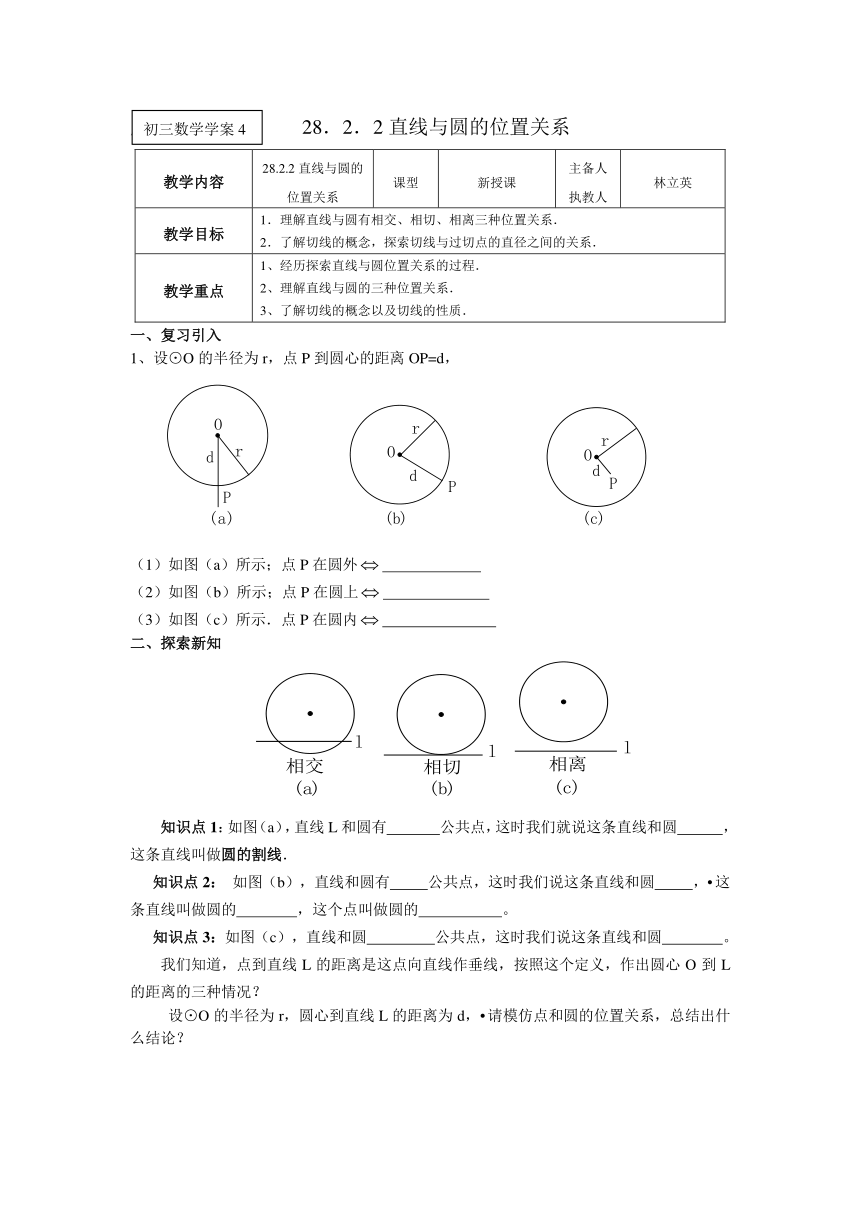
1、设⊙O的半径为r,点P到圆心的距离OP=d,
(1)如图(a)所示;点P在圆外
(2)如图(b)所示;点P在圆上
(3)如图(c)所示.点P在圆内
二、探索新知
知识点1:如图(a),直线L和圆有 公共点,这时我们就说这条直线和圆 ,这条直线叫做圆的割线.
知识点2: 如图(b),直线和圆有 公共点,这时我们说这条直线和圆 ,这条直线叫做圆的 ,这个点叫做圆的 。
知识点3:如图(c),直线和圆 公共点,这时我们说这条直线和圆 。
我们知道,点到直线L的距离是这点向直线作垂线,按照这个定义,作出圆心O到L的距离的三种情况?
设⊙O的半径为r,圆心到直线L的距离为d,请模仿点和圆的位置关系,总结出什么结论?
①如图(a)所示;直线L和⊙O d r,
②如图(b)所示; 直线L和⊙O
③如图(c)所示.直线L和⊙O
三、例题精讲
例1、在以C为圆心,r为半径的圆与直线有怎样的位置关系?为什么?
(1) (2) (3)
变式:r为何值时,⊙C与线段AB
(1)只有一个公共点? (2)有两个公共点?
(3)没有公共点? (4)有公共点?
小结:判断直线和圆的位置关系一般步骤是什么?
。
例2、如图,点A是一个半径为300m的润扬森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000m的笔直公路将两村连通。经测得
∠ABC=45°,∠ACB=30°,问此公路是否会穿过森林公园?请通过计算进行说明.
四、巩固练习:
1、⊙O的直径为4,圆心到直线L的距离为3,则直线L与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切或相交
2、⊙O的半径为5,点A在直线l上,若OA=5,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切或相交
3、设⊙O的半径为r,圆心到直线l的距离为d,若直线l与圆有公共点,则r与d的关系是( )
A、 B、 C、 D、
4、在以C为圆心,r为半径的圆与直线AB相切,则r= 。
5、如图,以o为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是 。
6、如图,⊙O的直径AB=8,弦CD=,且∥,判断以CD为直径的圆与直线AB有怎样的位置关系,为什么?
教学内容
28.2.2直线与圆的位置关系
课型
新授课
主备人
执教人
林立英
教学目标
1.理解直线与圆有相交、相切、相离三种位置关系.
2.了解切线的概念,探索切线与过切点的直径之间的关系.
教学重点
1、经历探索直线与圆位置关系的过程.
2、理解直线与圆的三种位置关系.
3、了解切线的概念以及切线的性质.
一、复习引入
1、设⊙O的半径为r,点P到圆心的距离OP=d,
(1)如图(a)所示;点P在圆外
(2)如图(b)所示;点P在圆上
(3)如图(c)所示.点P在圆内
二、探索新知
知识点1:如图(a),直线L和圆有 公共点,这时我们就说这条直线和圆 ,这条直线叫做圆的割线.
知识点2: 如图(b),直线和圆有 公共点,这时我们说这条直线和圆 ,这条直线叫做圆的 ,这个点叫做圆的 。
知识点3:如图(c),直线和圆 公共点,这时我们说这条直线和圆 。
我们知道,点到直线L的距离是这点向直线作垂线,按照这个定义,作出圆心O到L的距离的三种情况?
设⊙O的半径为r,圆心到直线L的距离为d,请模仿点和圆的位置关系,总结出什么结论?
①如图(a)所示;直线L和⊙O d r,
②如图(b)所示; 直线L和⊙O
③如图(c)所示.直线L和⊙O
三、例题精讲
例1、在以C为圆心,r为半径的圆与直线有怎样的位置关系?为什么?
(1) (2) (3)
变式:r为何值时,⊙C与线段AB
(1)只有一个公共点? (2)有两个公共点?
(3)没有公共点? (4)有公共点?
小结:判断直线和圆的位置关系一般步骤是什么?
。
例2、如图,点A是一个半径为300m的润扬森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000m的笔直公路将两村连通。经测得
∠ABC=45°,∠ACB=30°,问此公路是否会穿过森林公园?请通过计算进行说明.
四、巩固练习:
1、⊙O的直径为4,圆心到直线L的距离为3,则直线L与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切或相交
2、⊙O的半径为5,点A在直线l上,若OA=5,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切或相交
3、设⊙O的半径为r,圆心到直线l的距离为d,若直线l与圆有公共点,则r与d的关系是( )
A、 B、 C、 D、
4、在以C为圆心,r为半径的圆与直线AB相切,则r= 。
5、如图,以o为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是 。
6、如图,⊙O的直径AB=8,弦CD=,且∥,判断以CD为直径的圆与直线AB有怎样的位置关系,为什么?
