人教版2022年七年级数学下册5.2《平行线及其判定》 同步练习卷 (word版,含详解)
文档属性
| 名称 | 人教版2022年七年级数学下册5.2《平行线及其判定》 同步练习卷 (word版,含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 14:20:35 | ||
图片预览


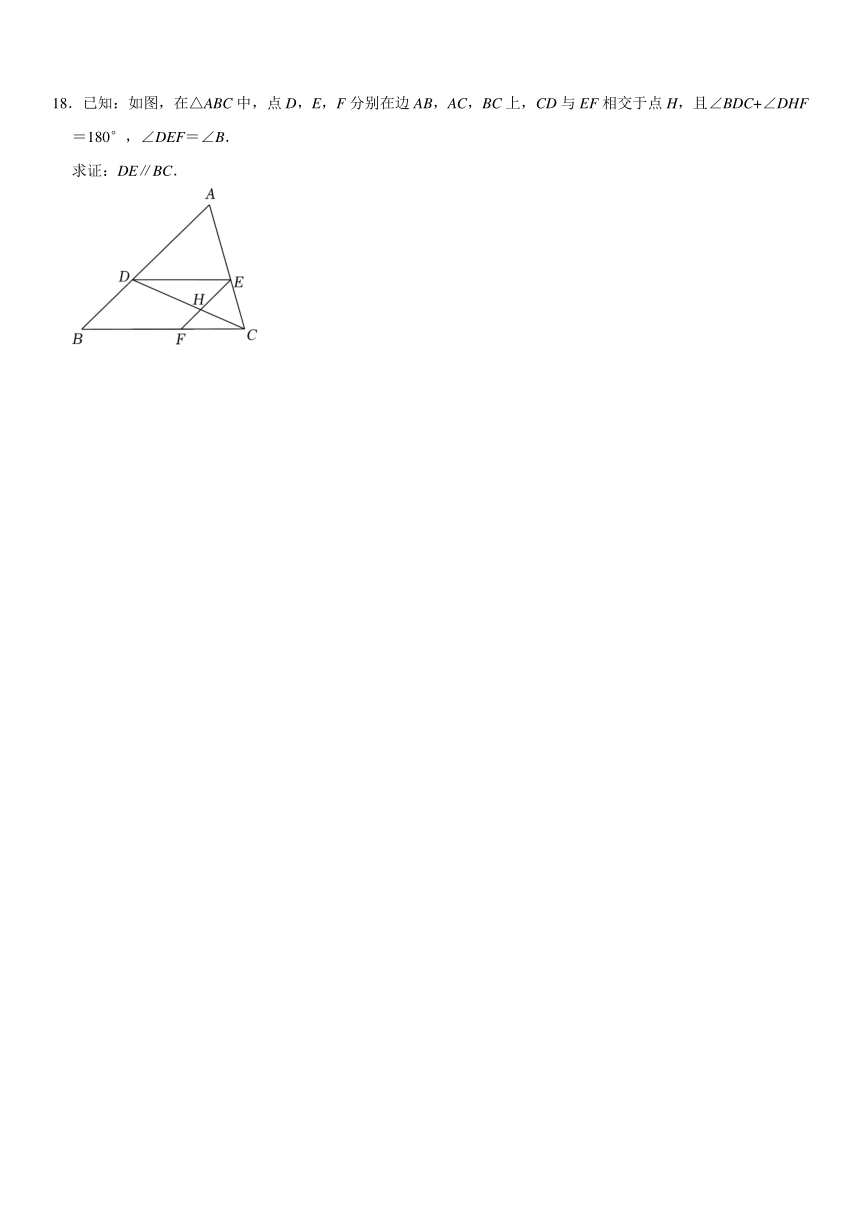
文档简介
人教版2022年七年级数学下册5.2《平行线及其判定》 同步练习卷
一.选择题
1.下列画出的直线a与b不一定平行的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.过直线上一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.直线外一点到该直线的所有线段中垂线最短
D.过直线外一点有且只有一条直线与已知直线平行
3.下列说法中正确的是( )
A.若a⊥b,b⊥c,则a⊥c
B.在同一平面内,不相交的两条线段必平行
C.两条直线被第三条直线所截,所得的同位角相等
D.两条平行线被第三条直线所截,一对内错角的角平分线互相平行
4.如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.EF∥BC B.AD∥BC C.AD∥EF D.AB∥CD
5.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠3=∠5 B.∠1=∠5 C.∠4+∠5=180° D.∠2=∠4
6.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
二.填空题
7.如图,在长方体ABCD﹣EFGH中,与面BCGF垂直,又与面EFGH平行的棱是 .
8.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
9.若AB∥CD,AB∥EF,则 ∥ ,理由是 .
10.如图,已知∠1=∠2,得到AB∥CD的依据是 .
11.如图,请添加一个条件,使得AB∥CD,添加一个符合要求的条件,可以是 .
12.如图,直线a,b被直线c所截,∠1=40°.要使a∥b,则∠2的度数应为 °.
13.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有 .
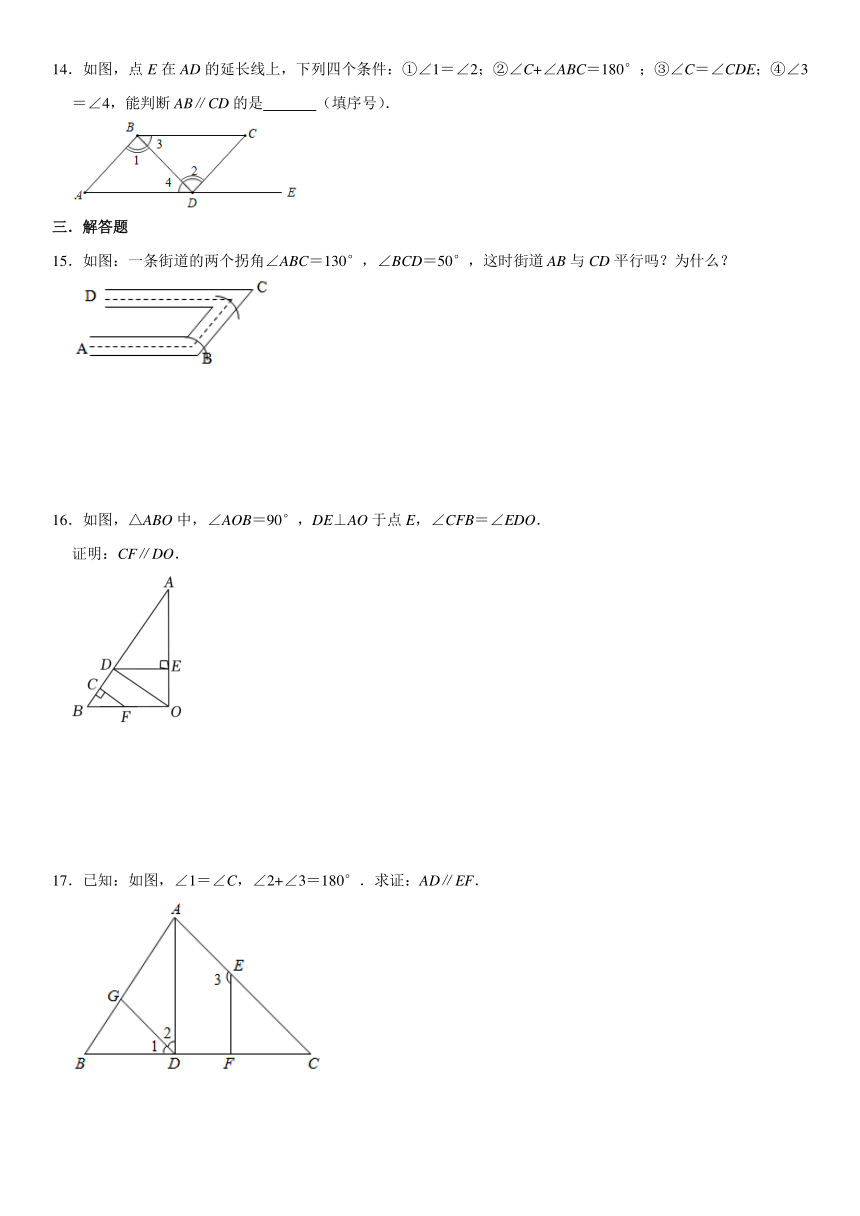
14.如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是 (填序号).
三.解答题
15.如图:一条街道的两个拐角∠ABC=130°,∠BCD=50°,这时街道AB与CD平行吗?为什么?
16.如图,△ABO中,∠AOB=90°,DE⊥AO于点E,∠CFB=∠EDO.
证明:CF∥DO.
17.已知:如图,∠1=∠C,∠2+∠3=180°.求证:AD∥EF.
18.已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°,∠DEF=∠B.
求证:DE∥BC.
参考答案
一.选择题
1.解:A.直线a与b不一定平行,故本选项符合题意;
B.根据同旁内角互补,两直线平行可得a∥b,故本选项不符合题意;
C.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
D.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
故选:A.
2.解:A、过直线外一点有且只有一条直线与已知直线平行,故原题说法错误;
B、同一平面内,不相交的两条直线叫做平行线,故原题说法错误;
C、直线外一点与该直线上所有点的连线中垂线最短,故原题说法错误;
D、过直线外一点有且只有一条直线与已知直线平行,故原题说法正确;
故选:D.
3.解:(1)∵a⊥b,b⊥c,∴a∥c,故A选项错误;
(2)两条不相交的直线必平行,但是线段的长是有限的,故不相交的两条线段不一定平行,故B选项错误;
(3)只有两条平行的直线被第三条直线所截,所得的同位角才相等,故C选项错误;
(4)如图:
∵AB∥CD,∴∠BEF=∠CFE.
∵EN平分∠BEF,FM平分∠CFE,
∴∠NEF=∠BEF,∠MFE=∠CFE,
∴∠NEF=∠MFE,∴EN∥FM.故D选项正确;
故选:D.
4.解:∵∠AEF=∠EFC,
∴AB∥CD,
故选:D.
5.解:A.∠3=∠5,可判定a∥b,不符合题意;
B.∠1=∠5,可判定a∥b,不符合题意;
C.∠4+∠5=180°,由同旁内角互补,两直线平行,可判定a∥b,不符合题意;
D.∠2=∠4,不能判定a∥b,符合题意.
故选:D.
6.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
二.填空题
7.解:如图,在长方体ABCD﹣EFGH中,与面BCGF垂直,又与面EFGH平行的棱是棱AB,棱CD.
故答案为:棱AB,棱CD.
8.解:已知OM∥a,ON∥a,所以点O、M、N三点共线的理由:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
9.解:∵AB∥CD,AB∥EF,
∴CD∥EF,
理由是:如果两条直线都和第三条直线平行,那么这两条直线平行,
故答案为平行于同一条直线的两条直线互相平行.
10.解:∵∠1和∠2是一对内错角,且∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行.
11.解:添加的条件可以是∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°.
∵∠BEF=∠C,
∴AB∥CD(同位角相等,两直线平行).
∵∠AEC=∠C,
∴AB∥CD(内错角相等,两直线平行).
∵∠BEC+∠C=180°,
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:∠BEF=∠C(答案不唯一).
12.解:∠3=180°﹣∠1=180°﹣40°=140°,
∵a∥b,
∴∠2=∠3=140°.
故答案为:140.
13.解:∵∠2=∠C,
∴EF∥CG,
又∵∠1=∠2,
∴∠1=∠C,
∴AB∥CD.
故答案为EF∥CG,AB∥CD.
14.解:①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
三.解答题
15.解:AB∥CD.理由如下:
∵∠ABC=130°,∠BCD=50°,
∴∠ABC+∠BCD=180°,
∴AB∥CD(同旁内角互补,两直线平行).
16.证明:∵DE⊥AO,
∴∠AED=90°,
∴∠AED=∠AOB=90°,
∴DE∥BO,
∴∠EDO=∠BOD,
∵∠EDO=∠CFB,
∴∠BOD=∠CFB,
∴CF∥DO.
17.证明:∵∠1=∠C,
∴GD∥AC,
∴∠CAD=∠2,
∵∠2+∠3=180°,
∴∠3+∠CAD=180°,
∴AD∥EF.
18.证明:∵∠BDC+∠DHF=180°,
∴BD∥FH,
∴∠B=∠EFC,
∵∠DEF=∠B,
∴∠EFC=∠DEF,
∴DE∥BC.
一.选择题
1.下列画出的直线a与b不一定平行的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.过直线上一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.直线外一点到该直线的所有线段中垂线最短
D.过直线外一点有且只有一条直线与已知直线平行
3.下列说法中正确的是( )
A.若a⊥b,b⊥c,则a⊥c
B.在同一平面内,不相交的两条线段必平行
C.两条直线被第三条直线所截,所得的同位角相等
D.两条平行线被第三条直线所截,一对内错角的角平分线互相平行
4.如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.EF∥BC B.AD∥BC C.AD∥EF D.AB∥CD
5.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠3=∠5 B.∠1=∠5 C.∠4+∠5=180° D.∠2=∠4
6.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
二.填空题
7.如图,在长方体ABCD﹣EFGH中,与面BCGF垂直,又与面EFGH平行的棱是 .
8.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
9.若AB∥CD,AB∥EF,则 ∥ ,理由是 .
10.如图,已知∠1=∠2,得到AB∥CD的依据是 .
11.如图,请添加一个条件,使得AB∥CD,添加一个符合要求的条件,可以是 .
12.如图,直线a,b被直线c所截,∠1=40°.要使a∥b,则∠2的度数应为 °.
13.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有 .
14.如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是 (填序号).
三.解答题
15.如图:一条街道的两个拐角∠ABC=130°,∠BCD=50°,这时街道AB与CD平行吗?为什么?
16.如图,△ABO中,∠AOB=90°,DE⊥AO于点E,∠CFB=∠EDO.
证明:CF∥DO.
17.已知:如图,∠1=∠C,∠2+∠3=180°.求证:AD∥EF.
18.已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°,∠DEF=∠B.
求证:DE∥BC.
参考答案
一.选择题
1.解:A.直线a与b不一定平行,故本选项符合题意;
B.根据同旁内角互补,两直线平行可得a∥b,故本选项不符合题意;
C.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
D.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
故选:A.
2.解:A、过直线外一点有且只有一条直线与已知直线平行,故原题说法错误;
B、同一平面内,不相交的两条直线叫做平行线,故原题说法错误;
C、直线外一点与该直线上所有点的连线中垂线最短,故原题说法错误;
D、过直线外一点有且只有一条直线与已知直线平行,故原题说法正确;
故选:D.
3.解:(1)∵a⊥b,b⊥c,∴a∥c,故A选项错误;
(2)两条不相交的直线必平行,但是线段的长是有限的,故不相交的两条线段不一定平行,故B选项错误;
(3)只有两条平行的直线被第三条直线所截,所得的同位角才相等,故C选项错误;
(4)如图:
∵AB∥CD,∴∠BEF=∠CFE.
∵EN平分∠BEF,FM平分∠CFE,
∴∠NEF=∠BEF,∠MFE=∠CFE,
∴∠NEF=∠MFE,∴EN∥FM.故D选项正确;
故选:D.
4.解:∵∠AEF=∠EFC,
∴AB∥CD,
故选:D.
5.解:A.∠3=∠5,可判定a∥b,不符合题意;
B.∠1=∠5,可判定a∥b,不符合题意;
C.∠4+∠5=180°,由同旁内角互补,两直线平行,可判定a∥b,不符合题意;
D.∠2=∠4,不能判定a∥b,符合题意.
故选:D.
6.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
二.填空题
7.解:如图,在长方体ABCD﹣EFGH中,与面BCGF垂直,又与面EFGH平行的棱是棱AB,棱CD.
故答案为:棱AB,棱CD.
8.解:已知OM∥a,ON∥a,所以点O、M、N三点共线的理由:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
9.解:∵AB∥CD,AB∥EF,
∴CD∥EF,
理由是:如果两条直线都和第三条直线平行,那么这两条直线平行,
故答案为平行于同一条直线的两条直线互相平行.
10.解:∵∠1和∠2是一对内错角,且∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行.
11.解:添加的条件可以是∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°.
∵∠BEF=∠C,
∴AB∥CD(同位角相等,两直线平行).
∵∠AEC=∠C,
∴AB∥CD(内错角相等,两直线平行).
∵∠BEC+∠C=180°,
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:∠BEF=∠C(答案不唯一).
12.解:∠3=180°﹣∠1=180°﹣40°=140°,
∵a∥b,
∴∠2=∠3=140°.
故答案为:140.
13.解:∵∠2=∠C,
∴EF∥CG,
又∵∠1=∠2,
∴∠1=∠C,
∴AB∥CD.
故答案为EF∥CG,AB∥CD.
14.解:①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
三.解答题
15.解:AB∥CD.理由如下:
∵∠ABC=130°,∠BCD=50°,
∴∠ABC+∠BCD=180°,
∴AB∥CD(同旁内角互补,两直线平行).
16.证明:∵DE⊥AO,
∴∠AED=90°,
∴∠AED=∠AOB=90°,
∴DE∥BO,
∴∠EDO=∠BOD,
∵∠EDO=∠CFB,
∴∠BOD=∠CFB,
∴CF∥DO.
17.证明:∵∠1=∠C,
∴GD∥AC,
∴∠CAD=∠2,
∵∠2+∠3=180°,
∴∠3+∠CAD=180°,
∴AD∥EF.
18.证明:∵∠BDC+∠DHF=180°,
∴BD∥FH,
∴∠B=∠EFC,
∵∠DEF=∠B,
∴∠EFC=∠DEF,
∴DE∥BC.
