人教版2022年七年级下册5.2《平行线及其判定》课后巩固训练卷(word,含解析)
文档属性
| 名称 | 人教版2022年七年级下册5.2《平行线及其判定》课后巩固训练卷(word,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 14:20:39 | ||
图片预览


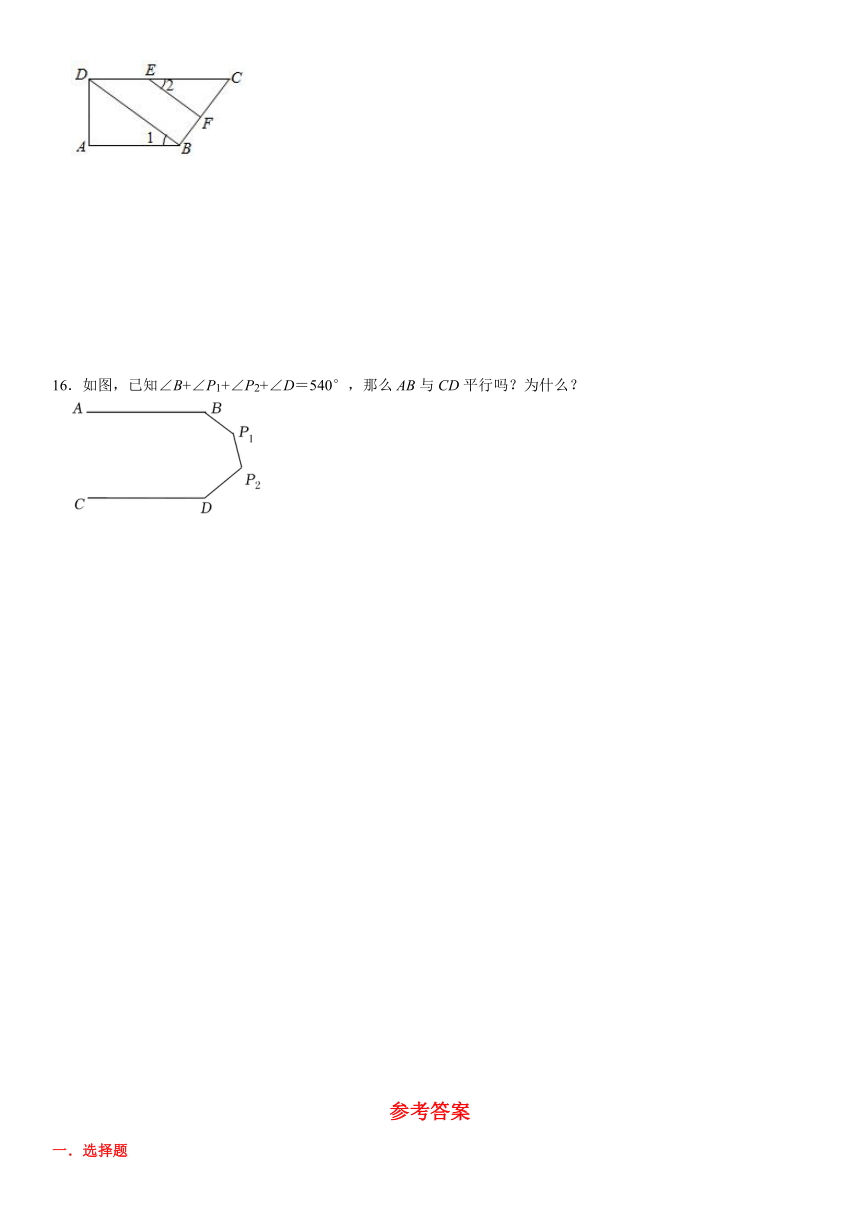
文档简介
人教版2022年七年级下册5.2《平行线及其判定》课后巩固训练卷
一.选择题
1.下列说法中,正确的是( )
A.两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,a∥c,则b∥c
D.两条直线不相交就平行
2.木条a、b、c如图用螺丝固定在木板α上且∠ABM=50°,∠DEM=70°,将木条a、木条b、木条c看作是在同一平面α内的三条直线AC、DF、MN,若使直线AC、直线DF达到平行的位置关系,则下列描述错误的是( )
A.木条b、c固定不动,木条a绕点B顺时针旋转20°
B.木条b、c固定不动,木条a绕点B逆时针旋转160°
C.木条a、c固定不动,木条b绕点E逆时针旋转20°
D.木条a、c固定不动,木条b绕点E顺时针旋转110°
3.如图,下列条件中能判定AB∥CE的是( )
A.∠A=∠ACE B.∠B=∠ACB C.∠A=∠ECD D.∠B=∠ACE
4.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行;
(2)同位角相等;
(3)不相交的两条射线叫做平行线;
(4)有公共顶点且有一条公共边的两个互补的角互为邻补角
A.4个 B.3个 C.2个 D.1个
5.如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定DE∥BC的个数是( )
①∠ADE=∠GBC;②∠DFB=∠GBC;③∠EDB+∠ABC=180°;④∠GFE=∠GBC.
A.1个 B.2个 C.3个 D.4个
二.填空题
6.如图,在长方体ABCD﹣EFGH中,与面ABCD垂直,又与面ADHE平行的棱是 .
7.若直线a∥b,a∥c,则直线b与c的位置关系是 .
8.如图,直线a,b被c所截,∠1=50°,若要a∥b,则需增加条件 (填图中某角的度数);依据是 .
9.如图,AB∥l,AC∥l,则A,B,C三点共线,理由是: .
10.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有 .
11.如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
三.解答题
12.将下列证明过程补充完整:
已知:如图,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
证明:∵CE平分∠ACD(已知),
∴∠2=∠ ( ).
∵∠1=∠2(已知),
∴∠1=∠ ( ).
∴AB∥CD( ).
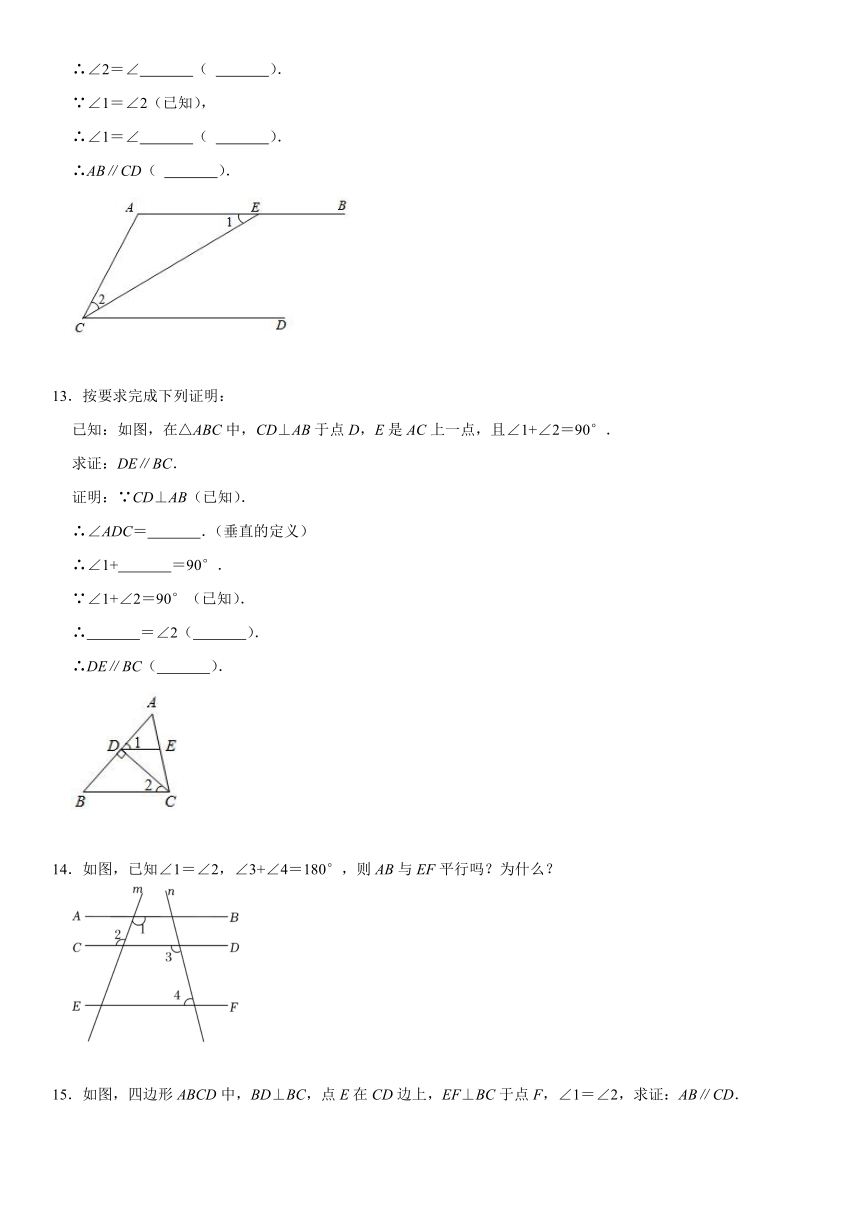
13.按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知).
∴∠ADC= .(垂直的定义)
∴∠1+ =90°.
∵∠1+∠2=90°(已知).
∴ =∠2( ).
∴DE∥BC( ).
14.如图,已知∠1=∠2,∠3+∠4=180°,则AB与EF平行吗?为什么?
15.如图,四边形ABCD中,BD⊥BC,点E在CD边上,EF⊥BC于点F,∠1=∠2,求证:AB∥CD.
16.如图,已知∠B+∠P1+∠P2+∠D=540°,那么AB与CD平行吗?为什么?
参考答案
一.选择题
1.解:A、在同一平面内不相交的两条直线叫做平行线,故本选项错误;
B、一条直线的平行线有无数条,故本选项错误;
C、若直线a∥b,a∥c,则b∥c,满足平行公理的推论,故本选项正确;
D、在同一平面内两条直线不相交就平行,故本选项错误.
故选:C.
2.解:A.木条b、c固定不动,木条a绕点B顺时针旋转20°,
∴∠ABE=50°+20°=70°=∠DEM,
∴AC∥DF,
故A不符合题意;
B.木条b、c固定不动,木条a绕点B逆时针旋转160°,
∴∠CBE=50°+20°=70°=∠DEM,
∴AC∥DF,
故B不符合题意;
C.木条a、c固定不动,木条b绕点E逆时针旋转20°,
∴∠DEM=70°﹣20°=50°=∠ABE,
∴AC∥DF,
故C不符合题意;
D.木条a、c固定不动,木条b绕点E顺时针旋转110°,
∴木条b和木条c重合,AC与DF不平行,
故D符合题意.
故选:D.
3.解:A、∵∠A=∠ACE,
∴AB∥CE,故A选项符合题意;
B、由∠B=∠ACB,不能判定AB∥CE,故B选项不符合题意;
C、由∠A=∠ECD,不能判定AB∥CE,故C选项不符合题意;
D、由∠B=∠ACE,不能判定AB∥CE,故D选项不符合题意;
故选:A.
4.解:(1)同一平面内,过一点有且只有一条直线与已知直线平行,故说法错误;
(2)两直线平行时,同位角才相等,故说法错误;
(3)同一平面内,不相交的两条射线叫做平行线,故说法错误;
(4)邻补角的定义是:两个角有公共边和公共顶点,一个角的一边是另一个角的一边的反向延长线,具有这样特点的两个角称就是邻补角,故说法错误.
故选:A.
5.解:①∠ADE=∠GBC不能判断DE∥BC;
②∵∠DFB=∠GBC,
∴DE∥BC;
③∵∠EDB+∠ABC=180°,
∴DE∥BC;
④∵∠GFE=∠GBC,
∴DE∥BC,
所以能判定DE∥BC的选项有②③④共3个,
故选:C.
二.填空题
6.解:如图,在长方体ABCD﹣EFGH中,与面ABCD垂直,又与面ADHE平行的棱是棱BF、棱CG.
故答案为:棱BF、棱CG.
7.解:若直线a∥b,a∥c,则直线b与c的位置关系是平行,
故答案为:平行.
8.解:∵∠3=50°,1=50°,
∴∠1=∠3,
∴a∥b(同位角相等,两直线平行).
故答案为:∠3=50°;同位角相等;两直线平行.
9.解:∵AB∥l,AC∥l,
∴A,B,C三点共线.
理由是:经过直线外一点,有且只有一条直线与这条直线平行.
故答案是:经过直线外一点,有且只有一条直线与这条直线平行.
10.解:∵∠2=∠C,
∴EF∥CG,
又∵∠1=∠2,
∴∠1=∠C,
∴AB∥CD.
故答案为EF∥CG,AB∥CD.
11.解:①中,∵∠1=∠3,∴AD∥BC(内错角相等,两直线平行),不合题意;
②中,∵∠5=∠B,∴AD∥BC(同位角相等,两直线平行),不合题意;
③中,∵∠1=∠4且AC平分∠DAB,∴∠2=∠4,∴AB∥CD,故此选项符合题意;
④中,∠B+∠BCD=180°,∴AB∥CD (同旁内角互补,两直线平行),故此选项符合题意;
故答案为:③④.
三.解答题
12.证明:∵CE平分∠ACD,
∴∠2=∠ECD(角平分线的定义),
∵∠1=∠2.(已知),
∴∠1=∠ECD(等量代换),
∴AB∥CD(内错角相等两直线平行).
故答案为:ECD;角平分线的定义;ECD;等量代换;内错角相等,两直线平行.
13.解:证明:∵CD⊥AB(已知),
∴∠ADC=90°(垂直的定义),
∴∠1+∠CDE=90°,
∵∠1+∠2=90°(已知),
∴∠CDE=∠2(同角的余角相等),
∴DE∥BC(内错角相等,两直线平行),
故答案为:90°;∠CDE;∠CDE,同角的余角相等;内错角相等,两直线平行.
14.解:AB∥EF,理由如下:
∵∠1=∠2,∠3+∠4=180°,
∴AB∥CD,CD∥EF,
∴AB∥EF.
15.证明:∵BD⊥BC,EF⊥BC,
∴BD∥EF,
∴∠BDC=∠2,
∵∠1=∠2,
∴∠1=∠BDC,
∴AB∥CD.
16.解:AB∥CD.理由如下:
过点P1作P1F∥AB,过点P2作P2G∥CD,
∴∠ABP1+∠BP1F=180°,∠CDP2+∠DP2G=180°,
∵∠B+∠P1+∠P2+∠D=540°,
∴∠FP1P2+∠P1P2G=180°,
∴P1F∥P2G(同旁内角互补,两直线平行),
∴AB∥CD.
一.选择题
1.下列说法中,正确的是( )
A.两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,a∥c,则b∥c
D.两条直线不相交就平行
2.木条a、b、c如图用螺丝固定在木板α上且∠ABM=50°,∠DEM=70°,将木条a、木条b、木条c看作是在同一平面α内的三条直线AC、DF、MN,若使直线AC、直线DF达到平行的位置关系,则下列描述错误的是( )
A.木条b、c固定不动,木条a绕点B顺时针旋转20°
B.木条b、c固定不动,木条a绕点B逆时针旋转160°
C.木条a、c固定不动,木条b绕点E逆时针旋转20°
D.木条a、c固定不动,木条b绕点E顺时针旋转110°
3.如图,下列条件中能判定AB∥CE的是( )
A.∠A=∠ACE B.∠B=∠ACB C.∠A=∠ECD D.∠B=∠ACE
4.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行;
(2)同位角相等;
(3)不相交的两条射线叫做平行线;
(4)有公共顶点且有一条公共边的两个互补的角互为邻补角
A.4个 B.3个 C.2个 D.1个
5.如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定DE∥BC的个数是( )
①∠ADE=∠GBC;②∠DFB=∠GBC;③∠EDB+∠ABC=180°;④∠GFE=∠GBC.
A.1个 B.2个 C.3个 D.4个
二.填空题
6.如图,在长方体ABCD﹣EFGH中,与面ABCD垂直,又与面ADHE平行的棱是 .
7.若直线a∥b,a∥c,则直线b与c的位置关系是 .
8.如图,直线a,b被c所截,∠1=50°,若要a∥b,则需增加条件 (填图中某角的度数);依据是 .
9.如图,AB∥l,AC∥l,则A,B,C三点共线,理由是: .
10.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有 .
11.如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
三.解答题
12.将下列证明过程补充完整:
已知:如图,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
证明:∵CE平分∠ACD(已知),
∴∠2=∠ ( ).
∵∠1=∠2(已知),
∴∠1=∠ ( ).
∴AB∥CD( ).
13.按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知).
∴∠ADC= .(垂直的定义)
∴∠1+ =90°.
∵∠1+∠2=90°(已知).
∴ =∠2( ).
∴DE∥BC( ).
14.如图,已知∠1=∠2,∠3+∠4=180°,则AB与EF平行吗?为什么?
15.如图,四边形ABCD中,BD⊥BC,点E在CD边上,EF⊥BC于点F,∠1=∠2,求证:AB∥CD.
16.如图,已知∠B+∠P1+∠P2+∠D=540°,那么AB与CD平行吗?为什么?
参考答案
一.选择题
1.解:A、在同一平面内不相交的两条直线叫做平行线,故本选项错误;
B、一条直线的平行线有无数条,故本选项错误;
C、若直线a∥b,a∥c,则b∥c,满足平行公理的推论,故本选项正确;
D、在同一平面内两条直线不相交就平行,故本选项错误.
故选:C.
2.解:A.木条b、c固定不动,木条a绕点B顺时针旋转20°,
∴∠ABE=50°+20°=70°=∠DEM,
∴AC∥DF,
故A不符合题意;
B.木条b、c固定不动,木条a绕点B逆时针旋转160°,
∴∠CBE=50°+20°=70°=∠DEM,
∴AC∥DF,
故B不符合题意;
C.木条a、c固定不动,木条b绕点E逆时针旋转20°,
∴∠DEM=70°﹣20°=50°=∠ABE,
∴AC∥DF,
故C不符合题意;
D.木条a、c固定不动,木条b绕点E顺时针旋转110°,
∴木条b和木条c重合,AC与DF不平行,
故D符合题意.
故选:D.
3.解:A、∵∠A=∠ACE,
∴AB∥CE,故A选项符合题意;
B、由∠B=∠ACB,不能判定AB∥CE,故B选项不符合题意;
C、由∠A=∠ECD,不能判定AB∥CE,故C选项不符合题意;
D、由∠B=∠ACE,不能判定AB∥CE,故D选项不符合题意;
故选:A.
4.解:(1)同一平面内,过一点有且只有一条直线与已知直线平行,故说法错误;
(2)两直线平行时,同位角才相等,故说法错误;
(3)同一平面内,不相交的两条射线叫做平行线,故说法错误;
(4)邻补角的定义是:两个角有公共边和公共顶点,一个角的一边是另一个角的一边的反向延长线,具有这样特点的两个角称就是邻补角,故说法错误.
故选:A.
5.解:①∠ADE=∠GBC不能判断DE∥BC;
②∵∠DFB=∠GBC,
∴DE∥BC;
③∵∠EDB+∠ABC=180°,
∴DE∥BC;
④∵∠GFE=∠GBC,
∴DE∥BC,
所以能判定DE∥BC的选项有②③④共3个,
故选:C.
二.填空题
6.解:如图,在长方体ABCD﹣EFGH中,与面ABCD垂直,又与面ADHE平行的棱是棱BF、棱CG.
故答案为:棱BF、棱CG.
7.解:若直线a∥b,a∥c,则直线b与c的位置关系是平行,
故答案为:平行.
8.解:∵∠3=50°,1=50°,
∴∠1=∠3,
∴a∥b(同位角相等,两直线平行).
故答案为:∠3=50°;同位角相等;两直线平行.
9.解:∵AB∥l,AC∥l,
∴A,B,C三点共线.
理由是:经过直线外一点,有且只有一条直线与这条直线平行.
故答案是:经过直线外一点,有且只有一条直线与这条直线平行.
10.解:∵∠2=∠C,
∴EF∥CG,
又∵∠1=∠2,
∴∠1=∠C,
∴AB∥CD.
故答案为EF∥CG,AB∥CD.
11.解:①中,∵∠1=∠3,∴AD∥BC(内错角相等,两直线平行),不合题意;
②中,∵∠5=∠B,∴AD∥BC(同位角相等,两直线平行),不合题意;
③中,∵∠1=∠4且AC平分∠DAB,∴∠2=∠4,∴AB∥CD,故此选项符合题意;
④中,∠B+∠BCD=180°,∴AB∥CD (同旁内角互补,两直线平行),故此选项符合题意;
故答案为:③④.
三.解答题
12.证明:∵CE平分∠ACD,
∴∠2=∠ECD(角平分线的定义),
∵∠1=∠2.(已知),
∴∠1=∠ECD(等量代换),
∴AB∥CD(内错角相等两直线平行).
故答案为:ECD;角平分线的定义;ECD;等量代换;内错角相等,两直线平行.
13.解:证明:∵CD⊥AB(已知),
∴∠ADC=90°(垂直的定义),
∴∠1+∠CDE=90°,
∵∠1+∠2=90°(已知),
∴∠CDE=∠2(同角的余角相等),
∴DE∥BC(内错角相等,两直线平行),
故答案为:90°;∠CDE;∠CDE,同角的余角相等;内错角相等,两直线平行.
14.解:AB∥EF,理由如下:
∵∠1=∠2,∠3+∠4=180°,
∴AB∥CD,CD∥EF,
∴AB∥EF.
15.证明:∵BD⊥BC,EF⊥BC,
∴BD∥EF,
∴∠BDC=∠2,
∵∠1=∠2,
∴∠1=∠BDC,
∴AB∥CD.
16.解:AB∥CD.理由如下:
过点P1作P1F∥AB,过点P2作P2G∥CD,
∴∠ABP1+∠BP1F=180°,∠CDP2+∠DP2G=180°,
∵∠B+∠P1+∠P2+∠D=540°,
∴∠FP1P2+∠P1P2G=180°,
∴P1F∥P2G(同旁内角互补,两直线平行),
∴AB∥CD.
