人教版数学七下5.1.2 .1垂线 课件(共38张PPT)
文档属性
| 名称 | 人教版数学七下5.1.2 .1垂线 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 697.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览




文档简介
(共38张PPT)
人教版 · 数学· 七年级(下)
第五章 相交线与平行线
5.1.2 垂线
第1课时 垂线及其性质
1.理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线。
2.掌握垂直的概念,能根据垂直求出角的度数。
3.掌握垂线的性质,并会利用所学知识进行简单的推理。
学习目标
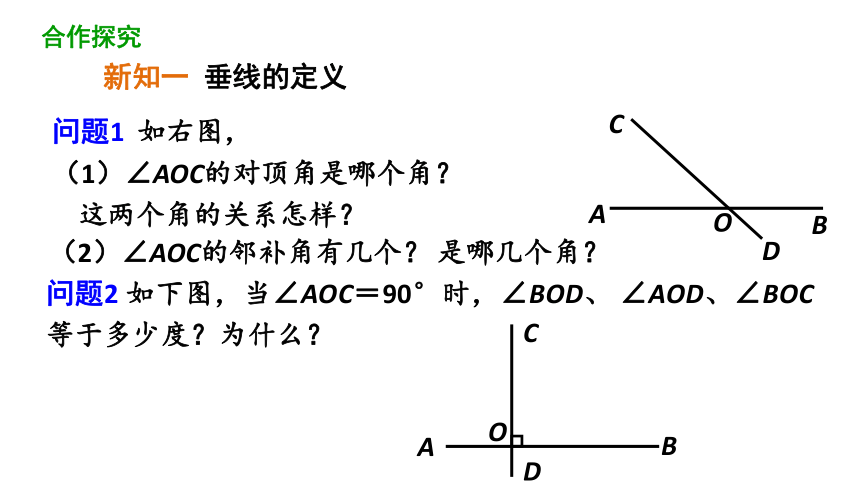
问题1 如右图,
(1)∠AOC的对顶角是哪个角?
这两个角的关系怎样?
(2)∠AOC的邻补角有几个? 是哪几个角?
问题2 如下图,当∠AOC=90°时,∠BOD、 ∠AOD、∠BOC等于多少度?为什么?
新知一 垂线的定义
A
C
B
D
O
A
B
C
D
O
合作探究
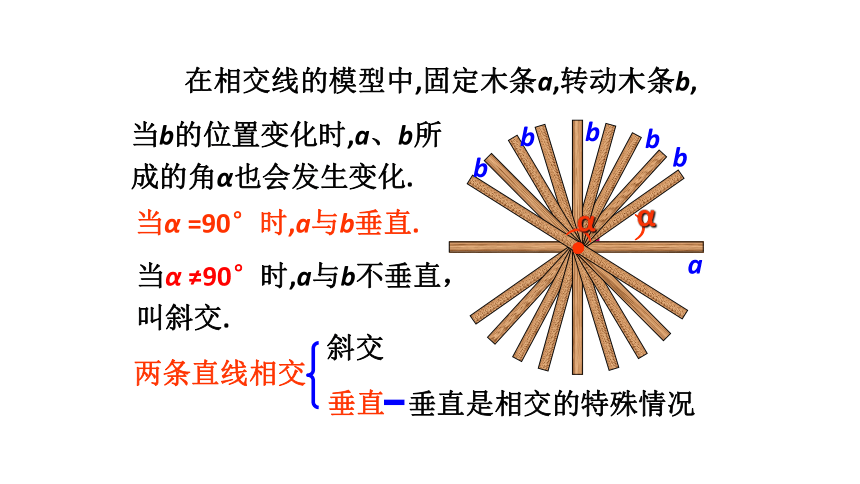
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
当两条直线相交所成的四个角中,有一个角是直角(90°)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
b
a
O
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中有一个角是直角.
1.垂直定义
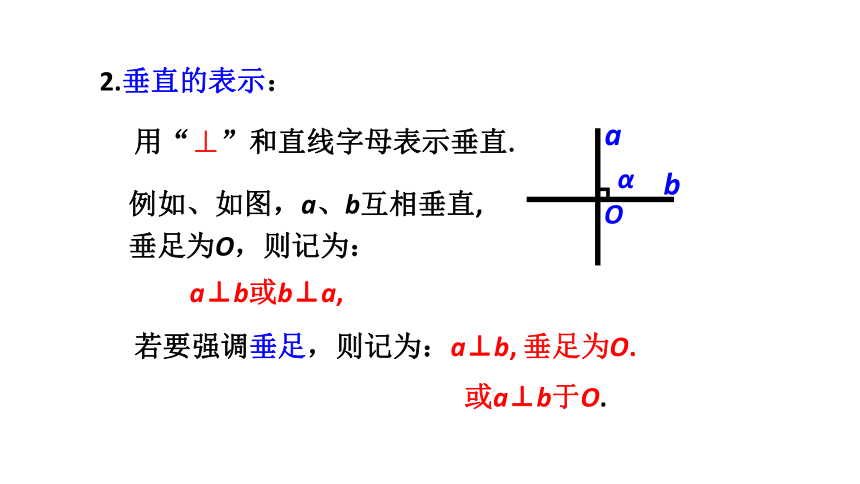
用“⊥”和直线字母表示垂直.
α
2.垂直的表示:
例如、如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b, 垂足为O.
或a⊥b于O.
b
a
O
F
E
M
N
O
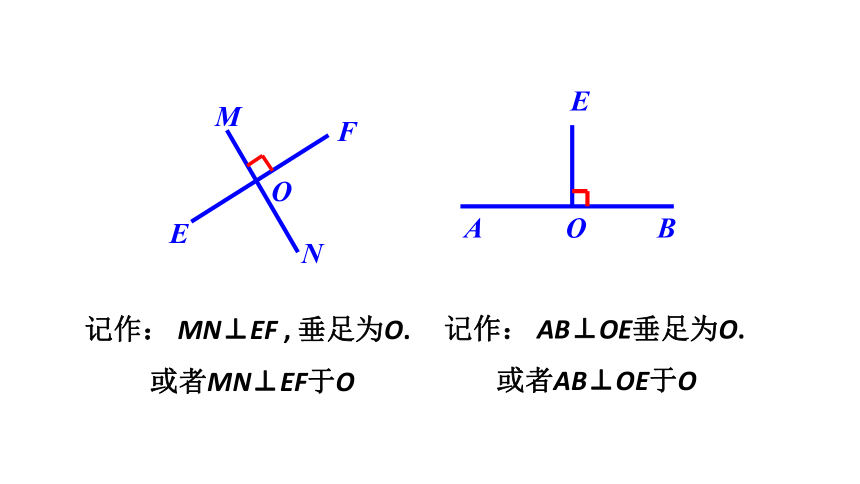
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于O
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
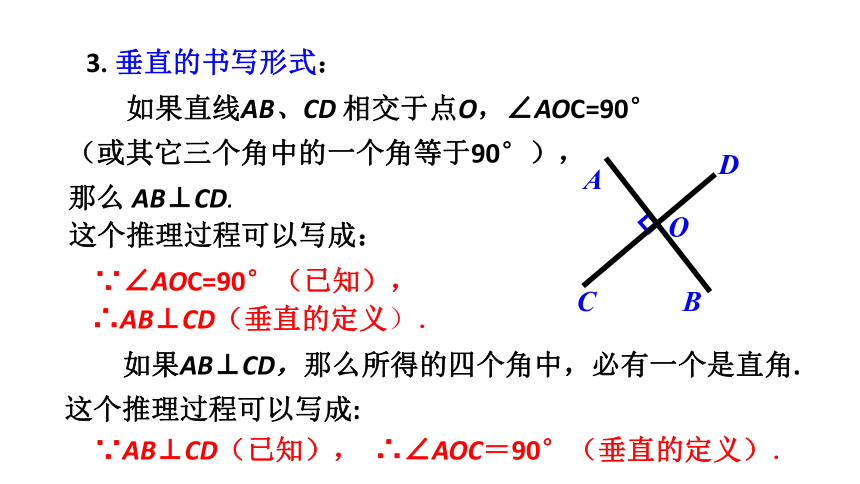
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),
那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知), ∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程可以写成:
A
B
C
D
O
3.垂直的书写形式:
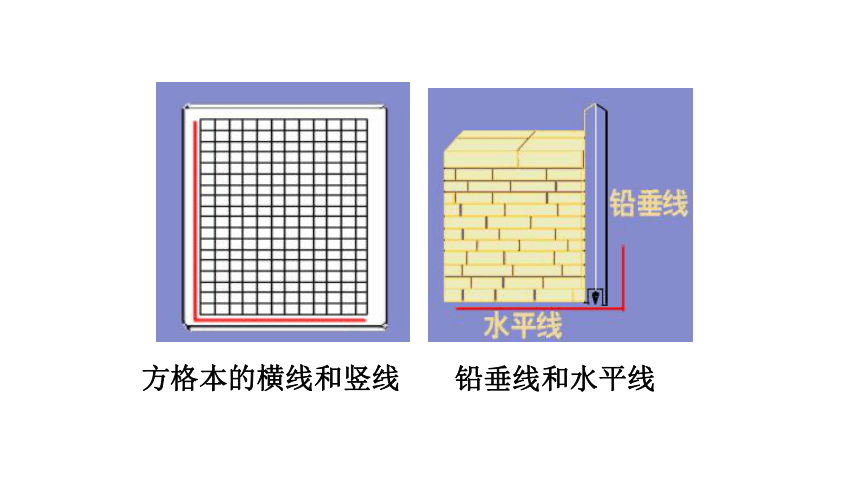
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
你能再举出其他例子吗
方格本的横线和竖线
铅垂线和水平线
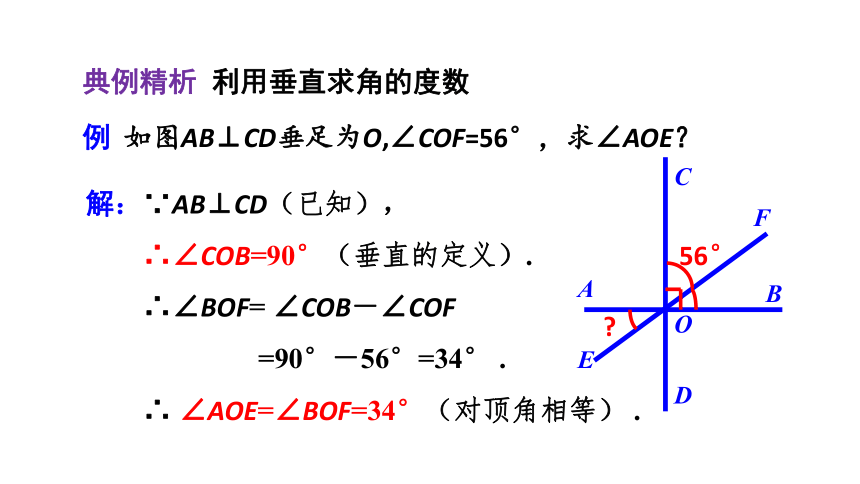
例 如图AB⊥CD垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等) .
F
E
D
C
B
A
O
56°
典例精析 利用垂直求角的度数
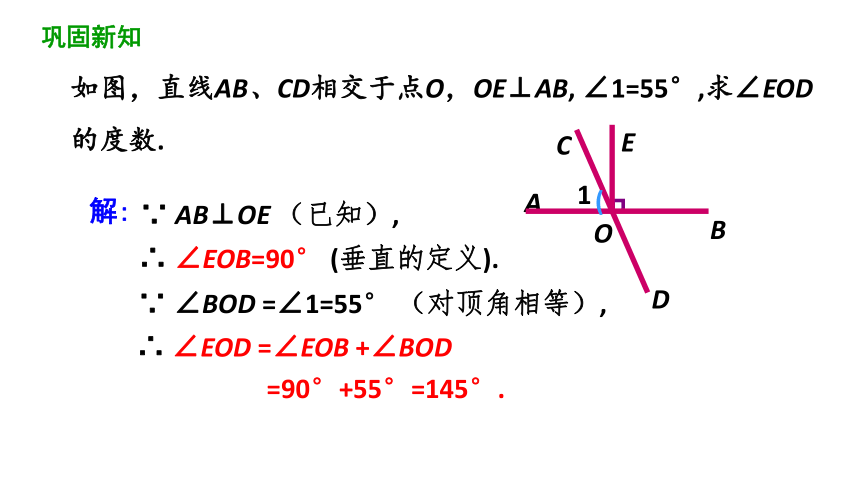
如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义).
∴ ∠EOD =∠EOB +∠BOD
=90°+55°=145°.
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知),
∵ ∠BOD =∠1=55° (对顶角相等),
解:
巩固新知
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
新知二 垂线的画法及其性质
合作探究
【讨论】这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
【讨论】这样画l的垂线可以画几条?
一条
l
B
C
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点B ,作l的垂线.
根据以上操作,你能得出什么结论?
【讨论】这样画l的垂线可以画几条?
一条
提示:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
归纳新知
1.(4分)如图,OA⊥OB,若∠1=55°,则∠2的度数为( )
A.35° B.40° C.45° D.60°
A
课堂练习
2.(4分)如图,若CD⊥EF,∠1=∠2,则AB⊥EF,请说明理由(补全解题过程).
解:因为CD⊥EF,
所以∠1=__________(垂直的定义).
所以∠2=∠1=__________.所以AB____EF(垂直的定义).
90°
90°
⊥
3.(4分)(河南中考)如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为____________.
140°
4.(6分)(教材P8习题T5变式)如图,直线AB,CD相交于点O,OE⊥CD,垂足为O,∠AOC=35°,求∠BOE的度数.
解:∵∠AOC=∠BOD,∠AOC=35°,
∴∠BOD=35°,
∵OE⊥CD,
∴∠EOD=90°,
∴∠BOE=∠EOD-∠BOD=90°-35°=55°
垂线的画法
5.(4分)下列选项中,利用三角板过点P画AB的垂线CD,正确的是( )
C
6.(4分)过线段外一点,画这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点
C.这条线段的延长线上 D.以上都有可能
D
7.(6分)(1)如图①,作AE⊥BC,CF⊥AD,垂足分别为E,F;
(2)如图②,分别过点P作垂线PC⊥OA,PD⊥OB,垂足分别为C,D.
解:(1)(2)如图所示:
8.(4分)【易错】在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
C
9.(4分)(教材P9习题T12变式)已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,那么A,B,C三点在同一条直线上,其理由是_____________________________________________________.
在同一平面内,过一点有且只有一条直线与已知直线垂直
1.(益阳中考)如图,直线AB,CD相交于点O,EO⊥CD.下列说法错误的是( )
A.∠AOD=∠BOC B.∠AOE+∠BOD=90°
C.∠AOC=∠AOE D.∠AOD+∠BOD=180°
C
课后练习
11.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOC=70°,则∠CON的度数为( )
A.65° B.55° C.45° D.35°
B
12.(三门峡期末)如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=72°,则∠AOF的度数为( )
A.72° B.60° C.54° D.36°
C
二、填空题(每小题5分,共10分)
13.如图所示,EO⊥CD,垂足为O,AB平分∠EOD,则∠BOD的度数为___________.
135°
14.【易错】在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是_________________.
60°或120°
16.(12分)如图所示,OM平分∠AOB,ON平分∠COD,OM⊥ON,∠BOC=26°,求∠AOD的度数.
解:因为OM平分∠AOB,ON平分∠COD,所以∠AOB=2∠AOM=2∠BOM,∠COD=2∠CON=2∠DON.因为OM⊥ON,所以∠MON=90°,所以∠CON+∠BOC+∠BOM=90°.因为∠BOC=26°,所以∠CON+∠BOM=90°-26°=64°,所以∠DON+∠AOM=64°.所以∠AOD=∠DON+∠AOM+∠MON=64°+90°=154°
【综合运用】
17.(13分)如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
再见
人教版 · 数学· 七年级(下)
第五章 相交线与平行线
5.1.2 垂线
第1课时 垂线及其性质
1.理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线。
2.掌握垂直的概念,能根据垂直求出角的度数。
3.掌握垂线的性质,并会利用所学知识进行简单的推理。
学习目标
问题1 如右图,
(1)∠AOC的对顶角是哪个角?
这两个角的关系怎样?
(2)∠AOC的邻补角有几个? 是哪几个角?
问题2 如下图,当∠AOC=90°时,∠BOD、 ∠AOD、∠BOC等于多少度?为什么?
新知一 垂线的定义
A
C
B
D
O
A
B
C
D
O
合作探究
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
当两条直线相交所成的四个角中,有一个角是直角(90°)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
b
a
O
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中有一个角是直角.
1.垂直定义
用“⊥”和直线字母表示垂直.
α
2.垂直的表示:
例如、如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b, 垂足为O.
或a⊥b于O.
b
a
O
F
E
M
N
O
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于O
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),
那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知), ∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程可以写成:
A
B
C
D
O
3.垂直的书写形式:
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
你能再举出其他例子吗
方格本的横线和竖线
铅垂线和水平线
例 如图AB⊥CD垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等) .
F
E
D
C
B
A
O
56°
典例精析 利用垂直求角的度数
如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义).
∴ ∠EOD =∠EOB +∠BOD
=90°+55°=145°.
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知),
∵ ∠BOD =∠1=55° (对顶角相等),
解:
巩固新知
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
新知二 垂线的画法及其性质
合作探究
【讨论】这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
【讨论】这样画l的垂线可以画几条?
一条
l
B
C
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点B ,作l的垂线.
根据以上操作,你能得出什么结论?
【讨论】这样画l的垂线可以画几条?
一条
提示:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
归纳新知
1.(4分)如图,OA⊥OB,若∠1=55°,则∠2的度数为( )
A.35° B.40° C.45° D.60°
A
课堂练习
2.(4分)如图,若CD⊥EF,∠1=∠2,则AB⊥EF,请说明理由(补全解题过程).
解:因为CD⊥EF,
所以∠1=__________(垂直的定义).
所以∠2=∠1=__________.所以AB____EF(垂直的定义).
90°
90°
⊥
3.(4分)(河南中考)如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为____________.
140°
4.(6分)(教材P8习题T5变式)如图,直线AB,CD相交于点O,OE⊥CD,垂足为O,∠AOC=35°,求∠BOE的度数.
解:∵∠AOC=∠BOD,∠AOC=35°,
∴∠BOD=35°,
∵OE⊥CD,
∴∠EOD=90°,
∴∠BOE=∠EOD-∠BOD=90°-35°=55°
垂线的画法
5.(4分)下列选项中,利用三角板过点P画AB的垂线CD,正确的是( )
C
6.(4分)过线段外一点,画这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点
C.这条线段的延长线上 D.以上都有可能
D
7.(6分)(1)如图①,作AE⊥BC,CF⊥AD,垂足分别为E,F;
(2)如图②,分别过点P作垂线PC⊥OA,PD⊥OB,垂足分别为C,D.
解:(1)(2)如图所示:
8.(4分)【易错】在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
C
9.(4分)(教材P9习题T12变式)已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,那么A,B,C三点在同一条直线上,其理由是_____________________________________________________.
在同一平面内,过一点有且只有一条直线与已知直线垂直
1.(益阳中考)如图,直线AB,CD相交于点O,EO⊥CD.下列说法错误的是( )
A.∠AOD=∠BOC B.∠AOE+∠BOD=90°
C.∠AOC=∠AOE D.∠AOD+∠BOD=180°
C
课后练习
11.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOC=70°,则∠CON的度数为( )
A.65° B.55° C.45° D.35°
B
12.(三门峡期末)如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=72°,则∠AOF的度数为( )
A.72° B.60° C.54° D.36°
C
二、填空题(每小题5分,共10分)
13.如图所示,EO⊥CD,垂足为O,AB平分∠EOD,则∠BOD的度数为___________.
135°
14.【易错】在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是_________________.
60°或120°
16.(12分)如图所示,OM平分∠AOB,ON平分∠COD,OM⊥ON,∠BOC=26°,求∠AOD的度数.
解:因为OM平分∠AOB,ON平分∠COD,所以∠AOB=2∠AOM=2∠BOM,∠COD=2∠CON=2∠DON.因为OM⊥ON,所以∠MON=90°,所以∠CON+∠BOC+∠BOM=90°.因为∠BOC=26°,所以∠CON+∠BOM=90°-26°=64°,所以∠DON+∠AOM=64°.所以∠AOD=∠DON+∠AOM+∠MON=64°+90°=154°
【综合运用】
17.(13分)如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
再见
