第二章整式的加减复习
图片预览










文档简介
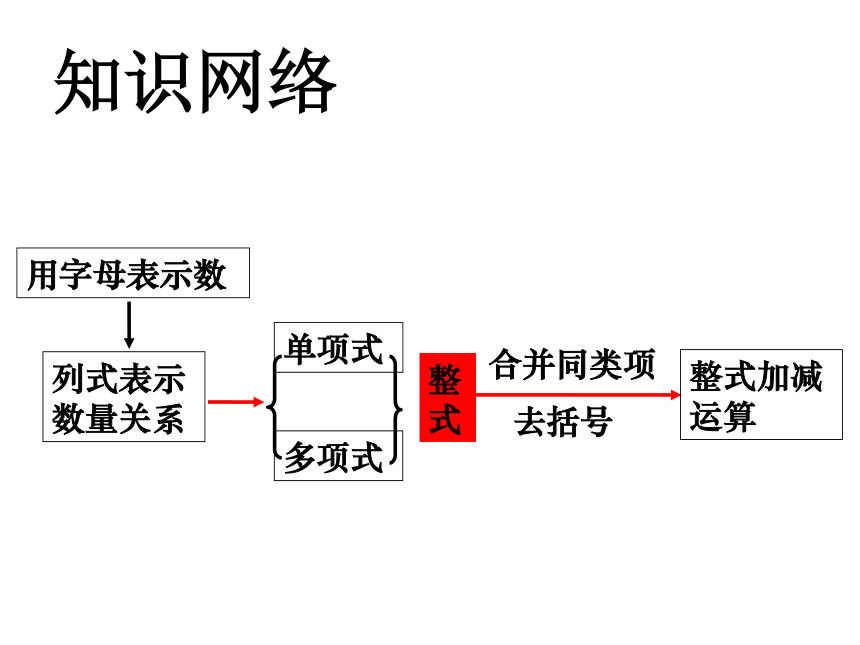
课件50张PPT。课题:整式复习江津区双福中学七年级数学组知识网络知识回顾整 式 的 加 减 单项式:多项式:去括号:同类项:合并同类项:整式的加减:系数、次数项、次数、常数项定义、“两相同、两无关”定义、法则、步骤法 则整 式步 骤3、 的项是( ),次数是( ),
的项是( ),次数是( ),是( )次( )项式。2、 的系数是( ),次数是( ), 的系数是
( ),次数是( );单项式有 多项式有
整式1、在式子: 中,哪些是单项式,哪些是多项式?哪些是整式?y2、1-x-5xy2 、-xy2、-x1-x-5xy2 y2、1-x-5xy2 、-x练 习(一):y21-x-5xy2 21、-x、-5xy2 返回通常我们把一个多项式的和项按照某个字母的指数人大到小(降幂)或者从小 到大(升幂)的顺序排列,如 也可以写成 。3、若5x2 y与是 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn同的和是单项式, m=( ) n=( )1、下列各组是不是同类项:练 习(二):-4x2+5x+55+5x-4x2(1) 4abc 与 4ab (2) -5 m2 n3 与 2n3 m2(3) -0.3 x2 y 与 y x22、合并下列同类项:(1) 3xy – 4 xy – xy = ( ) (2) -a-a-2a=( )
(3) 0.8ab3 - a3 b+0.2ab3 =( )不是是是 –2xy –4aab3 - a3 b 2 1 2 1返回
3、多项式 与 的和是 ,它们的差
是 ,多项式 减去一个多项 后是 ,则
这个多项式是 。1、去括号:(1) +(x-3)= (2) -(x-3)=
(3)-(x+5y-2)= (4)+(3x-5y+6z)=练 习(三):x-3-x+3- x- 5y+2 3x-5y+6z2、计算:(1)x-(-y -z+1)=
( 2 ) m+(-n+q)= ;
( 3 ) a - ( b+c-3)= ;
( 4 ) x+(5-3y)= 。
x-5xy2 -3x+xy2 -5a+4ab32aX+y +z -1m-n+qa-b-c+3x+5-3y-2x-4xy2 4x-6xy2 -7a+4ab3列代数式要注意以下几点:数字与字母、字母与字母相乘,要把乘号省略;如:2×a写作2a、a×b写作ab、 2×(a+b)或( a+b)×2写作 2(a+b).1.返回3 指出下列代数式中哪些是单项式?哪些是多项式?哪些是整式?[例1] 评析:本题需应用单项式、多项式、整式的意义来解答。单项式只含有“乘积”运算;多项式必须含有加法或减法运算。不论单项式还是多项式,分母中都不能含有字母。解:单项式有:多项式有:整式有:3、 的项是( ),次数是( ),
的项是( ),次数是( ),是( )次( )项式。2、 的系数是( ),次数是( ), 的系数是
( ),次数是( );单项式有 多项式有
整式1、在式子: 中,哪些是单项式,哪些是多项式?哪些是整式?y2、1-x-5xy2 、-xy2、-x1-x-5xy2 y2、1-x-5xy2 、-x练 习(一):y21-x-5xy2 21、-x、-5xy2 [例2] 评析:对含有两个或两个以上字母的多项式重新排列,先要确定是按哪个字母升(降)幂排列,再将常数项或不含这个字母的项按照升幂排在第一项,降幂排在最后一项。(1)按x的升幂排列;(2)按y的降幂排列。解:(1)按x的升幂排列:(2)按y的降幂排列:[例1] 若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。[例2]如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。思考:计算(1)-a2-a2-a2;(2)a3+a2b+ab2-a2b-ab2-b2(1)用代数式表示“比a的平方的2倍小1的数”
为( )
A.2a2-1 B.(2a)2-1
C.2(a-1)2 D.(2a-1)2A二、列代数式降了40% a, 则降价
后此药的价格是:
a -40% a = (1- 40%)a(2).将原价为a的某种常用药降价40%,
则降价后此药的价格是____元. (1- 40%)a三、基本概念运用:3ba(2)下列各组中,同类项是( )
A.3x2y与-3xy2 B.3xy与-2yx
C.2x与2x2 D.5xy与5yzB324.下列式子正确的是( ).D基础练习2ab2-8x3xa+b-c-da-b+c-d12x-6-5+x12a -12b4x+3所含______相同,并且__________的指数也相同的项叫做同类项。字母相同的字母把多项式中的_______合并成一项,叫做合并同类项。 同类项负变正不变,要变全都变 整式加减的法则:有括号就先________,然后再__________。去括号合并同类项1、若mxpyq与-3xy2p+1的差为 ,
求pq(p+q)的值。解: ∴ mxpyq与-3xy2p+1必为同类项根据同类项的定义有 p=1,q=2p+1=3。 pq(p+q)=1×3(1+3)=12 [典例] ∵ mxpyq与-3xy2p+1的差为 当p=1,q=3时 答:pq(p+q)=12 6.如果关于x的多项式 的值与x
无关,则a的取值为_____.解:原式=由题意知,则:6a-6=0∴a=117.如果关于x,y的多项式 的差
不含有二次项,求 的值。解:原式=由题意知,则: m-3=0
2+2n=0∴m=3,n=-1;∴ = =-1探索题 (1) 一个三位数,十位数字的值a,个位数字比十位数字的3倍多1,百位数字比个位数字少3,试用多项式表示这个三位数,当a=2时,这个三位数是多少?解: 100(3a+1-3)+10a+(3a+1)
=313a-199
当a=2时,原式=313×2-199=427[典例] 若 是同类项,
求 的值。 解:根据同类项定义,有2m-1=5且m+n=1
解得 m=3,n=-2。
则(mn+5)2008=[3×(-2)+5]2008=(-1)2008=1
答:(mn+5)2008=1。评析:此题要求含m、n的代数式的值,但题目中没有给出m、n的值。需要从同类项的概念出发,先求出m、n的值,从而求出代数式的值。同时注意乘方性质的应用。5. 化简(5a-3b) -3(a2-2b )解: (5a-3b) -3(a2-2b )
= 5a-3b -(3 a2 -6b )
熟练后此式可省略
= 5a-3b - 3 a2 +6b
括号前是负要变号
=5a+3b - 3 a2
同类项记得要合并
注意!
正确使用
乘法分配律典型例题1、计算:(1)(2)解:原式===解:原式===活动三例9: 求 的值
其中 x=-2, y= 时.→去括号→合并同类项﹜﹜将式子化简再代入数值进行
计算3.化简: (1)x-3(1-2x+x2)+2(-2+3x-x2)评析:注意去多重括号的顺序。有同类项的要合并。解:(1)原式=x-3+6x-3x2-4+6x-2x2
=(-3x2-2x2)+(x+6x+6x)+(-3-4)
=-5x2+13x-7(2)原式=3x2-5xy+{-x2-[-3xy+2x2-2xy+y2]}
=3x2-5xy+{-x2+3xy-2x2+2xy-y2}
=3x2-5xy-x2+3xy-2x2+2xy-y2
=(3x2-x2-2x2)+(-5xy+3xy+2xy)-y2=-y2(2)(3x2-5xy)+{-x2-[-3xy+2(x2-xy)+y2]} 1.变式训练智力挑战 礼堂第一排有(a-1)个座位,后面每排都比前一排多1个座位.
(1).第二排有__________个座位.
(2).第三排有__________个座位.
(3).第n排有多少个座位?a(a+1)解:分析 第1排 (a-1) 个第2排 (a-1)+1=a 个 第3排 (a-1)+2=a+1 个第4排 (a-1)+3 =a+2 个
第n排的座位 (a-1)+ =a-1+n-1=a+n-2 (个)思考:当a=20,n=19时的座位数是多少?(37)(n-1)三、易错题精讲 [典例] 已知A=4x2-4xy+y2,B=x2+xy-5y2,求A-B。评析:本题产生错误的原因是把A、B代入所求式子时,丢掉了括号,导致后两项的符号错误。因为A、B表示两个多项式,它是一个整体,代入式子时必须用括号表示,尤其是括号前面是“-”时,如果丢掉了括号就会发生符号错误,今后遇到这类问题,一定要记住“添括号”。错解:A-B=4x2-4xy+y2-x2+xy-5y2=3x2-3xy-4y2正解:A-B=(4x2-4xy+y2)-(x2+xy-5y2)
=4x2-4xy+y2-x2-xy+5y2
=3x2-5xy+6y2思考:求多项式x2-7x-2与-2x2+4x-1的差。解先化简,再求值格式应正确,步骤要清楚求值:[典例] 化简求值:(基本题型) (2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3。评析:此类题目的基本思路是:先化简—即去括号合并同类项,再求值—用数字代替相应的字母,进行有理数的运算。解:原式=2x3-xyz-2x3+2y3-2xyz+xyz-2y3
=(2x3-2x3)+(2y3-2y3)+(-2xyz-xyz+xyz)
=-2xyz
当x=1,y=2,z=-3时,原式=-2×1×2×(-3)=12[典例] 化简求值:(基本题型) (2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3。评析:此类题目的基本思路是:先化简—即去括号合并同类项,再求值—用数字代替相应的字母,进行有理数的运算。解:原式=2x3-xyz-2x3+2y3-2xyz+xyz-2y3
=(2x3-2x3)+(2y3-2y3)+(-2xyz-xyz+xyz)
=-2xyz
当x=1,y=2,z=-3时,原式=-2×1×2×(-3)=12[典例] 已知(x+1)2+|y-1|=0,求下列式子的值。
2(xy-5xy2)-(3xy2-xy)解:根据非负数的性质,有x+1=0且y-1=0,
∴ x=-1,y=1。则2(xy-5xy2)-(3xy2-xy)
=2xy-10xy2-3xy2+xy
=3xy-13xy2
当x=-1,y=1时,原式=3×(-1)×1-13×(-1)×12
=-3+13=10评析:根据已知条件,由非负数的性质,先求出x、y的值,这是求值的关键,然后代入化简后的代数式,进行求值。思考:已知A=3a2+2b2,B=a2-2a-b2,求当(b+4)2+|a-3|=0时,A-B的值。[典例] 已知2x+3y-1=0,求3-6x-9y的值。解:∵2x+3y-1=0,∴2x+3y=1。
∴3-6x-9y=3-(6x+9y)=3-3(2x+3y)=3-3×1=0
答:所求代数式的值为0。评析:学习了添括号法则后,对于某些求值问题灵活应用添括号的方法,可化难为易。如本题,虽然没有给出x、y的取值,但利用添括号和整体代入,求值问题迎刃而解。注意体会和掌握这种方法。思考:把多项式x3-6x2y+12xy2-8y3+1,写成两个整式的和,使其中一个不含字母x。[典例1] 已知2x+3y-1=0,求3-6x-9y的值。解:∵2x+3y-1=0,∴2x+3y=1。
∴3-6x-9y=3-(6x+9y)=3-3(2x+3y)=3-3×1=0
答:所求代数式的值为0。评析:学习了添括号法则后,对于某些求值问题灵活应用添括号的方法,可化难为易。如本题,虽然没有给出x、y的取值,但利用添括号和整体代入,求值问题迎刃而解。注意体会和掌握这种方法。[练习] 已知3x2-x=1,求7-9x2+3x的值。解 7-9x2+3x=7-(9x2-3x)=7-3(3x2-x)=7-3×1=4四、妙法揭示 [典例] 设x2+xy=3,xy+y2=-2,求2x2-xy-3y2的值。解:∵x2+xy=3,∴2(x2+xy)=6,即2x2+2xy=6
∴ 2x2-xy-3y2=2x2+2xy-3xy-3y2
=(2x2+2xy)-(3xy+3y2)
=(2x2+2xy)-3(xy+y2)
=6-3×(-2)=6+6=12评析:利用所给条件,对多项式进行拆项、重新分组是解此类题的关键。分组时要添括号,按添括号法则进行,注意符号的变化及分配律的应用。思考:设3x2-x=1,求9x4+12x3-3x2-7x+2000的值。(3)定义运算:a※b=ab+a+b-1,
验证下列运算成立的是( )
A.a※b=(-a)※(-b)
B.a※(-b)=(-a)※b
C.a※b=b※a
D.a※(b※c)=(a※b)※c C(-a).(-b)-a-b-1a.(-b)+a-b-1-a.b-a+b-1ba+b+a-11.某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。该商场为促销制定了如下两种优惠方式:第一种:买一支毛笔附赠一本书法练习本;第二种:按购买金额打九折付款。八年级(5)班的小明想为本班书法兴趣小组购买这种毛笔10支,书法练习本 x(x≥10)本。
(2).若小明想为本班书法兴趣小组购买书法练习本30 本,试问小明应该选择哪一种优惠方式才更省钱? (2).25×10+5(x-10) =25×10+5(30-10) =350(25×10+5x) ×90%解:把X=30分别代入两个代数式:(25×10+5×30) ×90% =360所以选择第一种优惠方式[典例] 有人说:“下面代数式的值的大小与a、b的取值无关”,你认为这句话正确吗?为什么? 解:这句话正确。理由如下:因为结果是一个常数项,与a、b的取值无关,所以这句话是正确的。还有其它规律吗?返回5.如图,在2005年3月的日历上:(3)用一个十字框
任意框出5个数,
设中间一个数为
a,则框出的5个数
的和为 . 5a填写对折次数与所得层数和所得折痕数的变化关系表: 探究活动二将一张普通的报纸对折,可得到一条折痕。继续对折,对折时每次折痕与上次的折痕保持平行。连续对折4次后,可以得到几条折痕?如果对折10次呢?对折n次呢。248162N2N -173115…… 1、当x=2,y=-1999时,哪位同学能以最快的速度求出多项式 x-xy- x+xy+1的值。 2、求代数式的值:8p2 -7q+6q - 7p2 –7,其中p=3,
q=3。3、有这样一道题:“当a=13.58,b=9.07 时,求多项式7a3 - 6a3b+3a2b+3a3+6a3b - 3a2b - 10a3 的值。”1、探索规律并填空:
(1) .....
。 思考:(2)计算: .2、小丽做一道数学题:“已知两个多项式A,B,B为4x2-5x-6,求A+B.”,小丽把A+B看成A-B计算结果是-7x2+10x+12.根据以上信息,你能求出A+B的结果吗?相信你准能想出办法!5、礼堂第1排有a个座位,后面每排都比前一排多1个座位,第二排有多少个座位?第3排呢?用m表示第n 排座位数,m是多少?当a=20,n =19时,计算m的值。分析:第一排有a个座位,第二排有( )个座位,第三排有( )个座位?第4排有( )个座位。所以第n 排有 个座位,即m= ,a+1a+2a+3[a+(n-1)]a+n-1a=-2,b=11
的项是( ),次数是( ),是( )次( )项式。2、 的系数是( ),次数是( ), 的系数是
( ),次数是( );单项式有 多项式有
整式1、在式子: 中,哪些是单项式,哪些是多项式?哪些是整式?y2、1-x-5xy2 、-xy2、-x1-x-5xy2 y2、1-x-5xy2 、-x练 习(一):y21-x-5xy2 21、-x、-5xy2 返回通常我们把一个多项式的和项按照某个字母的指数人大到小(降幂)或者从小 到大(升幂)的顺序排列,如 也可以写成 。3、若5x2 y与是 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn同的和是单项式, m=( ) n=( )1、下列各组是不是同类项:练 习(二):-4x2+5x+55+5x-4x2(1) 4abc 与 4ab (2) -5 m2 n3 与 2n3 m2(3) -0.3 x2 y 与 y x22、合并下列同类项:(1) 3xy – 4 xy – xy = ( ) (2) -a-a-2a=( )
(3) 0.8ab3 - a3 b+0.2ab3 =( )不是是是 –2xy –4aab3 - a3 b 2 1 2 1返回
3、多项式 与 的和是 ,它们的差
是 ,多项式 减去一个多项 后是 ,则
这个多项式是 。1、去括号:(1) +(x-3)= (2) -(x-3)=
(3)-(x+5y-2)= (4)+(3x-5y+6z)=练 习(三):x-3-x+3- x- 5y+2 3x-5y+6z2、计算:(1)x-(-y -z+1)=
( 2 ) m+(-n+q)= ;
( 3 ) a - ( b+c-3)= ;
( 4 ) x+(5-3y)= 。
x-5xy2 -3x+xy2 -5a+4ab32aX+y +z -1m-n+qa-b-c+3x+5-3y-2x-4xy2 4x-6xy2 -7a+4ab3列代数式要注意以下几点:数字与字母、字母与字母相乘,要把乘号省略;如:2×a写作2a、a×b写作ab、 2×(a+b)或( a+b)×2写作 2(a+b).1.返回3 指出下列代数式中哪些是单项式?哪些是多项式?哪些是整式?[例1] 评析:本题需应用单项式、多项式、整式的意义来解答。单项式只含有“乘积”运算;多项式必须含有加法或减法运算。不论单项式还是多项式,分母中都不能含有字母。解:单项式有:多项式有:整式有:3、 的项是( ),次数是( ),
的项是( ),次数是( ),是( )次( )项式。2、 的系数是( ),次数是( ), 的系数是
( ),次数是( );单项式有 多项式有
整式1、在式子: 中,哪些是单项式,哪些是多项式?哪些是整式?y2、1-x-5xy2 、-xy2、-x1-x-5xy2 y2、1-x-5xy2 、-x练 习(一):y21-x-5xy2 21、-x、-5xy2 [例2] 评析:对含有两个或两个以上字母的多项式重新排列,先要确定是按哪个字母升(降)幂排列,再将常数项或不含这个字母的项按照升幂排在第一项,降幂排在最后一项。(1)按x的升幂排列;(2)按y的降幂排列。解:(1)按x的升幂排列:(2)按y的降幂排列:[例1] 若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。评析:例1要注意同类项概念的应用;例2要注意几位数的表示方法。如:578=5×100+7×10+8。[例2]如果一个两位数的个位数是十位数的4倍,那么这个两位数一定是7的倍数。请说明理由。解:设两位数的十位数字是x,则它的个位数字是4x。
∴这个两位数可表示为:10x+4x=14x,
∵14x是7的倍数,故这个两位数是7的倍数。思考:计算(1)-a2-a2-a2;(2)a3+a2b+ab2-a2b-ab2-b2(1)用代数式表示“比a的平方的2倍小1的数”
为( )
A.2a2-1 B.(2a)2-1
C.2(a-1)2 D.(2a-1)2A二、列代数式降了40% a, 则降价
后此药的价格是:
a -40% a = (1- 40%)a(2).将原价为a的某种常用药降价40%,
则降价后此药的价格是____元. (1- 40%)a三、基本概念运用:3ba(2)下列各组中,同类项是( )
A.3x2y与-3xy2 B.3xy与-2yx
C.2x与2x2 D.5xy与5yzB324.下列式子正确的是( ).D基础练习2ab2-8x3xa+b-c-da-b+c-d12x-6-5+x12a -12b4x+3所含______相同,并且__________的指数也相同的项叫做同类项。字母相同的字母把多项式中的_______合并成一项,叫做合并同类项。 同类项负变正不变,要变全都变 整式加减的法则:有括号就先________,然后再__________。去括号合并同类项1、若mxpyq与-3xy2p+1的差为 ,
求pq(p+q)的值。解: ∴ mxpyq与-3xy2p+1必为同类项根据同类项的定义有 p=1,q=2p+1=3。 pq(p+q)=1×3(1+3)=12 [典例] ∵ mxpyq与-3xy2p+1的差为 当p=1,q=3时 答:pq(p+q)=12 6.如果关于x的多项式 的值与x
无关,则a的取值为_____.解:原式=由题意知,则:6a-6=0∴a=117.如果关于x,y的多项式 的差
不含有二次项,求 的值。解:原式=由题意知,则: m-3=0
2+2n=0∴m=3,n=-1;∴ = =-1探索题 (1) 一个三位数,十位数字的值a,个位数字比十位数字的3倍多1,百位数字比个位数字少3,试用多项式表示这个三位数,当a=2时,这个三位数是多少?解: 100(3a+1-3)+10a+(3a+1)
=313a-199
当a=2时,原式=313×2-199=427[典例] 若 是同类项,
求 的值。 解:根据同类项定义,有2m-1=5且m+n=1
解得 m=3,n=-2。
则(mn+5)2008=[3×(-2)+5]2008=(-1)2008=1
答:(mn+5)2008=1。评析:此题要求含m、n的代数式的值,但题目中没有给出m、n的值。需要从同类项的概念出发,先求出m、n的值,从而求出代数式的值。同时注意乘方性质的应用。5. 化简(5a-3b) -3(a2-2b )解: (5a-3b) -3(a2-2b )
= 5a-3b -(3 a2 -6b )
熟练后此式可省略
= 5a-3b - 3 a2 +6b
括号前是负要变号
=5a+3b - 3 a2
同类项记得要合并
注意!
正确使用
乘法分配律典型例题1、计算:(1)(2)解:原式===解:原式===活动三例9: 求 的值
其中 x=-2, y= 时.→去括号→合并同类项﹜﹜将式子化简再代入数值进行
计算3.化简: (1)x-3(1-2x+x2)+2(-2+3x-x2)评析:注意去多重括号的顺序。有同类项的要合并。解:(1)原式=x-3+6x-3x2-4+6x-2x2
=(-3x2-2x2)+(x+6x+6x)+(-3-4)
=-5x2+13x-7(2)原式=3x2-5xy+{-x2-[-3xy+2x2-2xy+y2]}
=3x2-5xy+{-x2+3xy-2x2+2xy-y2}
=3x2-5xy-x2+3xy-2x2+2xy-y2
=(3x2-x2-2x2)+(-5xy+3xy+2xy)-y2=-y2(2)(3x2-5xy)+{-x2-[-3xy+2(x2-xy)+y2]} 1.变式训练智力挑战 礼堂第一排有(a-1)个座位,后面每排都比前一排多1个座位.
(1).第二排有__________个座位.
(2).第三排有__________个座位.
(3).第n排有多少个座位?a(a+1)解:分析 第1排 (a-1) 个第2排 (a-1)+1=a 个 第3排 (a-1)+2=a+1 个第4排 (a-1)+3 =a+2 个
第n排的座位 (a-1)+ =a-1+n-1=a+n-2 (个)思考:当a=20,n=19时的座位数是多少?(37)(n-1)三、易错题精讲 [典例] 已知A=4x2-4xy+y2,B=x2+xy-5y2,求A-B。评析:本题产生错误的原因是把A、B代入所求式子时,丢掉了括号,导致后两项的符号错误。因为A、B表示两个多项式,它是一个整体,代入式子时必须用括号表示,尤其是括号前面是“-”时,如果丢掉了括号就会发生符号错误,今后遇到这类问题,一定要记住“添括号”。错解:A-B=4x2-4xy+y2-x2+xy-5y2=3x2-3xy-4y2正解:A-B=(4x2-4xy+y2)-(x2+xy-5y2)
=4x2-4xy+y2-x2-xy+5y2
=3x2-5xy+6y2思考:求多项式x2-7x-2与-2x2+4x-1的差。解先化简,再求值格式应正确,步骤要清楚求值:[典例] 化简求值:(基本题型) (2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3。评析:此类题目的基本思路是:先化简—即去括号合并同类项,再求值—用数字代替相应的字母,进行有理数的运算。解:原式=2x3-xyz-2x3+2y3-2xyz+xyz-2y3
=(2x3-2x3)+(2y3-2y3)+(-2xyz-xyz+xyz)
=-2xyz
当x=1,y=2,z=-3时,原式=-2×1×2×(-3)=12[典例] 化简求值:(基本题型) (2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3。评析:此类题目的基本思路是:先化简—即去括号合并同类项,再求值—用数字代替相应的字母,进行有理数的运算。解:原式=2x3-xyz-2x3+2y3-2xyz+xyz-2y3
=(2x3-2x3)+(2y3-2y3)+(-2xyz-xyz+xyz)
=-2xyz
当x=1,y=2,z=-3时,原式=-2×1×2×(-3)=12[典例] 已知(x+1)2+|y-1|=0,求下列式子的值。
2(xy-5xy2)-(3xy2-xy)解:根据非负数的性质,有x+1=0且y-1=0,
∴ x=-1,y=1。则2(xy-5xy2)-(3xy2-xy)
=2xy-10xy2-3xy2+xy
=3xy-13xy2
当x=-1,y=1时,原式=3×(-1)×1-13×(-1)×12
=-3+13=10评析:根据已知条件,由非负数的性质,先求出x、y的值,这是求值的关键,然后代入化简后的代数式,进行求值。思考:已知A=3a2+2b2,B=a2-2a-b2,求当(b+4)2+|a-3|=0时,A-B的值。[典例] 已知2x+3y-1=0,求3-6x-9y的值。解:∵2x+3y-1=0,∴2x+3y=1。
∴3-6x-9y=3-(6x+9y)=3-3(2x+3y)=3-3×1=0
答:所求代数式的值为0。评析:学习了添括号法则后,对于某些求值问题灵活应用添括号的方法,可化难为易。如本题,虽然没有给出x、y的取值,但利用添括号和整体代入,求值问题迎刃而解。注意体会和掌握这种方法。思考:把多项式x3-6x2y+12xy2-8y3+1,写成两个整式的和,使其中一个不含字母x。[典例1] 已知2x+3y-1=0,求3-6x-9y的值。解:∵2x+3y-1=0,∴2x+3y=1。
∴3-6x-9y=3-(6x+9y)=3-3(2x+3y)=3-3×1=0
答:所求代数式的值为0。评析:学习了添括号法则后,对于某些求值问题灵活应用添括号的方法,可化难为易。如本题,虽然没有给出x、y的取值,但利用添括号和整体代入,求值问题迎刃而解。注意体会和掌握这种方法。[练习] 已知3x2-x=1,求7-9x2+3x的值。解 7-9x2+3x=7-(9x2-3x)=7-3(3x2-x)=7-3×1=4四、妙法揭示 [典例] 设x2+xy=3,xy+y2=-2,求2x2-xy-3y2的值。解:∵x2+xy=3,∴2(x2+xy)=6,即2x2+2xy=6
∴ 2x2-xy-3y2=2x2+2xy-3xy-3y2
=(2x2+2xy)-(3xy+3y2)
=(2x2+2xy)-3(xy+y2)
=6-3×(-2)=6+6=12评析:利用所给条件,对多项式进行拆项、重新分组是解此类题的关键。分组时要添括号,按添括号法则进行,注意符号的变化及分配律的应用。思考:设3x2-x=1,求9x4+12x3-3x2-7x+2000的值。(3)定义运算:a※b=ab+a+b-1,
验证下列运算成立的是( )
A.a※b=(-a)※(-b)
B.a※(-b)=(-a)※b
C.a※b=b※a
D.a※(b※c)=(a※b)※c C(-a).(-b)-a-b-1a.(-b)+a-b-1-a.b-a+b-1ba+b+a-11.某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。该商场为促销制定了如下两种优惠方式:第一种:买一支毛笔附赠一本书法练习本;第二种:按购买金额打九折付款。八年级(5)班的小明想为本班书法兴趣小组购买这种毛笔10支,书法练习本 x(x≥10)本。
(2).若小明想为本班书法兴趣小组购买书法练习本30 本,试问小明应该选择哪一种优惠方式才更省钱? (2).25×10+5(x-10) =25×10+5(30-10) =350(25×10+5x) ×90%解:把X=30分别代入两个代数式:(25×10+5×30) ×90% =360所以选择第一种优惠方式[典例] 有人说:“下面代数式的值的大小与a、b的取值无关”,你认为这句话正确吗?为什么? 解:这句话正确。理由如下:因为结果是一个常数项,与a、b的取值无关,所以这句话是正确的。还有其它规律吗?返回5.如图,在2005年3月的日历上:(3)用一个十字框
任意框出5个数,
设中间一个数为
a,则框出的5个数
的和为 . 5a填写对折次数与所得层数和所得折痕数的变化关系表: 探究活动二将一张普通的报纸对折,可得到一条折痕。继续对折,对折时每次折痕与上次的折痕保持平行。连续对折4次后,可以得到几条折痕?如果对折10次呢?对折n次呢。248162N2N -173115…… 1、当x=2,y=-1999时,哪位同学能以最快的速度求出多项式 x-xy- x+xy+1的值。 2、求代数式的值:8p2 -7q+6q - 7p2 –7,其中p=3,
q=3。3、有这样一道题:“当a=13.58,b=9.07 时,求多项式7a3 - 6a3b+3a2b+3a3+6a3b - 3a2b - 10a3 的值。”1、探索规律并填空:
(1) .....
。 思考:(2)计算: .2、小丽做一道数学题:“已知两个多项式A,B,B为4x2-5x-6,求A+B.”,小丽把A+B看成A-B计算结果是-7x2+10x+12.根据以上信息,你能求出A+B的结果吗?相信你准能想出办法!5、礼堂第1排有a个座位,后面每排都比前一排多1个座位,第二排有多少个座位?第3排呢?用m表示第n 排座位数,m是多少?当a=20,n =19时,计算m的值。分析:第一排有a个座位,第二排有( )个座位,第三排有( )个座位?第4排有( )个座位。所以第n 排有 个座位,即m= ,a+1a+2a+3[a+(n-1)]a+n-1a=-2,b=11
