2021-2022学年北师大版七年级数学下册第二章相交线与平行线单元测试卷(二)(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册第二章相交线与平行线单元测试卷(二)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 259.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 14:50:58 | ||
图片预览



文档简介
2021-2022学年七年级数学下册(北师大版)
第二章 相交线与平行线单元测试卷(二)
一、单选题
1.下列说法正确的是( )
A.同位角相等 B.在同一平面内,如果⊥,⊥,则⊥
C.相等的角是对顶角 D.在同一平面内,如果∥,∥,则∥
2.如图,下列说法中错误的是( )
A.∠3与∠5是同位角 B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角 D.∠1和∠5是同位角
3.a、b、c是平面上的任意三条直线,它们的交点可以有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.以上都不正确
4.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm
C.大于3cm D.大于或等于3cm
5.如图,AB∥CD,若EM平分∠BEF,FM平分∠EFD,EN平分∠AEF,则与∠BEM互余的角有( ).
A.6个 B.5个
C.4个 D.3个
6.如图,三角形DEF是由三角形ABC通过平移得到的,且点B,E,C,F在同一直线上.若BF=14,CE=6,则BE的长是( )
A.2 B.4 C.5 D.3
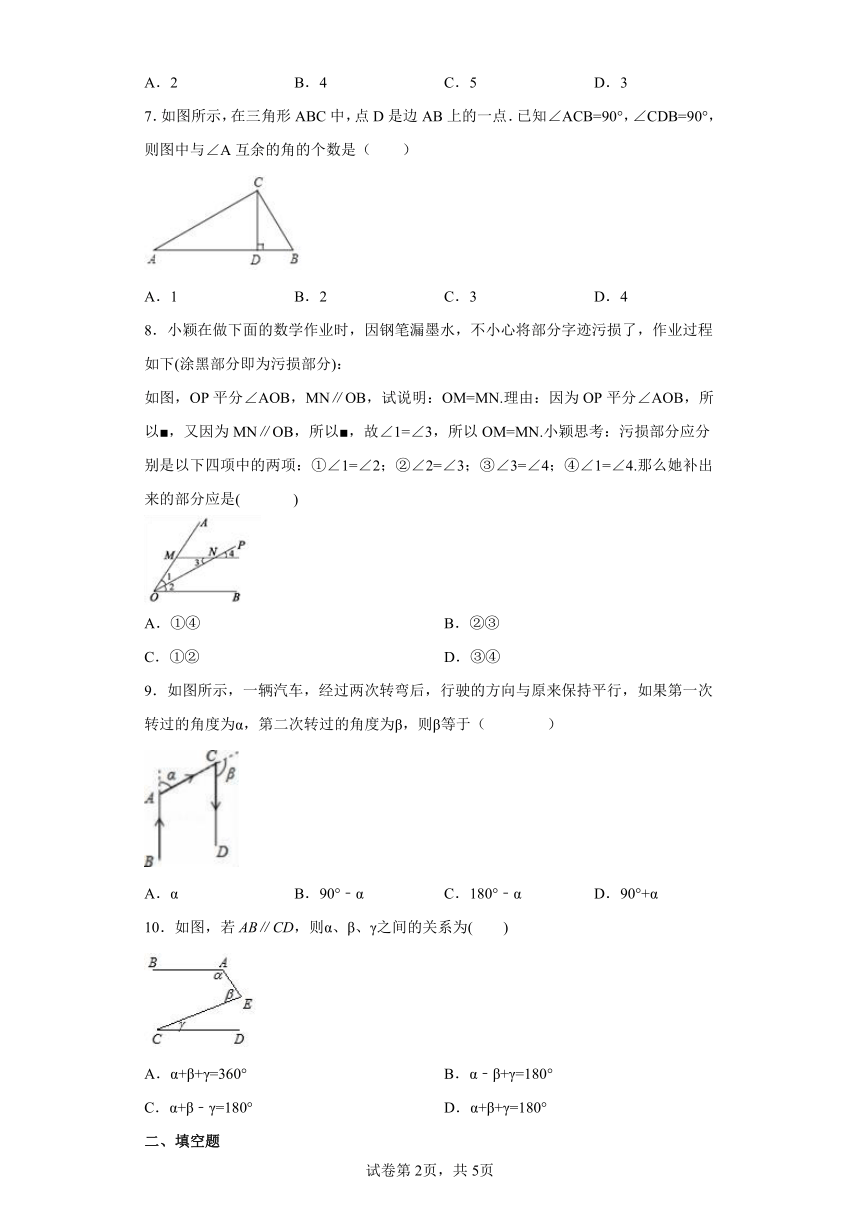
7.如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是( )
A.1 B.2 C.3 D.4
8.小颖在做下面的数学作业时,因钢笔漏墨水,不小心将部分字迹污损了,作业过程如下(涂黑部分即为污损部分):
如图,OP平分∠AOB,MN∥OB,试说明:OM=MN.理由:因为OP平分∠AOB,所以■,又因为MN∥OB,所以■,故∠1=∠3,所以OM=MN.小颖思考:污损部分应分别是以下四项中的两项:①∠1=∠2;②∠2=∠3;③∠3=∠4;④∠1=∠4.那么她补出来的部分应是( )
A.①④ B.②③
C.①② D.③④
9.如图所示,一辆汽车,经过两次转弯后,行驶的方向与原来保持平行,如果第一次转过的角度为α,第二次转过的角度为β,则β等于( )
A.α B.90°﹣α C.180°﹣α D.90°+α
10.如图,若AB∥CD,则α、β、γ之间的关系为( )
A.α+β+γ=360° B.α﹣β+γ=180°
C.α+β﹣γ=180° D.α+β+γ=180°
二、填空题
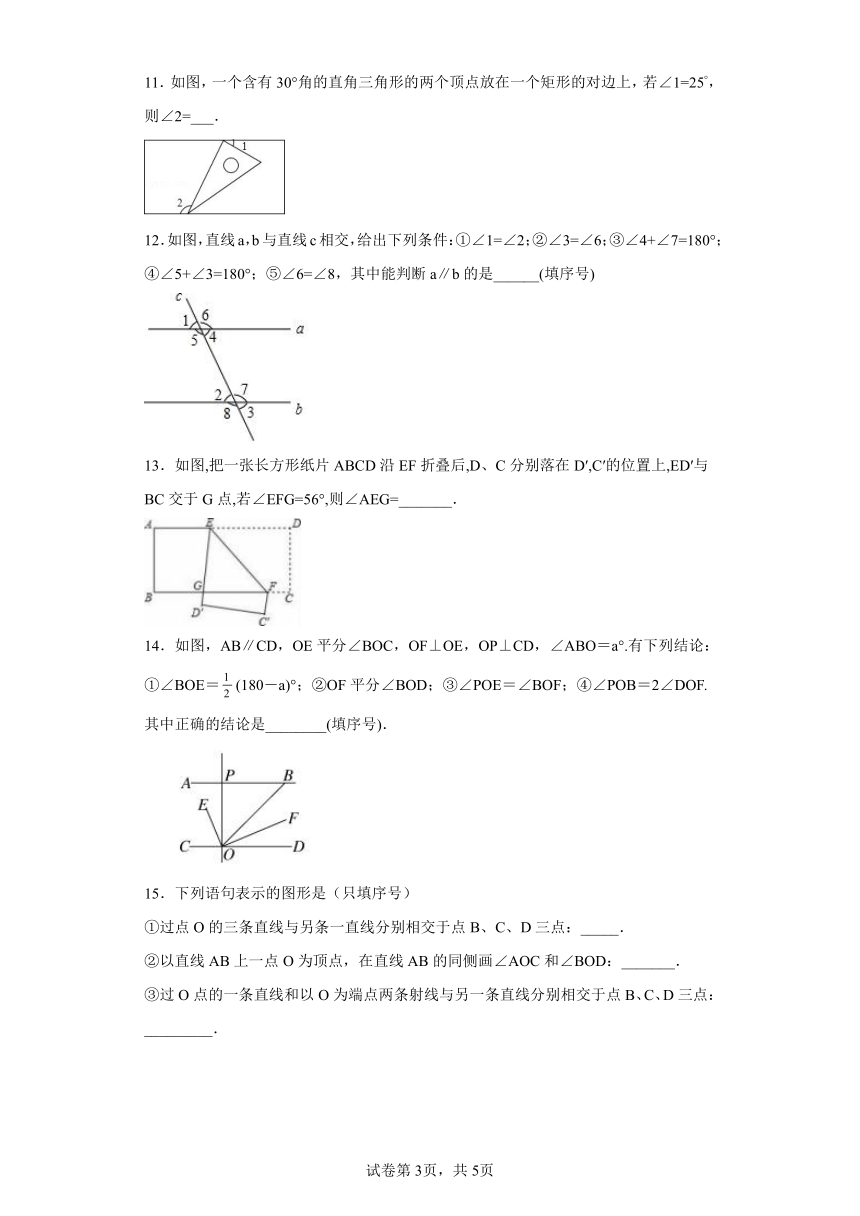
11.如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=___.
12.如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°;⑤∠6=∠8,其中能判断a∥b的是______(填序号)
13.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=56°,则∠AEG=_______.
14.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是________(填序号).
15.下列语句表示的图形是(只填序号)
①过点O的三条直线与另条一直线分别相交于点B、C、D三点:_____.
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:_______.
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:_________.
三、解答题
16.将直尺与三角尺按如图所示的方式叠放在一起.在图中标记的角中,写出所有与互余的角.
17.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
18.已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
19.如图,已知射线与直线交于点,平分,于,,且.
(1)求的度数;
(2)试说明平分.
20.如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.
试卷第1页,共3页
试卷第5页,共5页
参考答案:
1.D
【解析】
解:A选项只有在两直线平行时同位角相等,故A选项错误;
B选项在同一平面内,如果⊥,⊥,则,而不是⊥,故B选项错误;
C选项对顶角一定相等,但相等的角不一定是对顶角,故C选项错误;
D选项在同一平面内,如果∥,∥,则∥,故D选项正确.
故选:D.
2.D
【解析】
∠1和∠5不是同位角,D选项错误.
故选D.
3.B
【解析】
a、b、c是平面上的任意三条直线,①它们可以相交于1点,
②a∥b,b,c相交于一点,故它们的交点为2点,
③a、b、c两两相交于不同点,交点为3个,
④a∥b∥c,它们有0个交点,
故选B.
4.D
【解析】
试题解析:A到直线MN的距离是3cm,根据点到直线距离的定义,3cm表示垂线段的长度,根据垂线段最短,其它线段的长度大于或等于3cm,
故选D.
5.B
【解析】
∵AB∥CD,
∴∠AEF+∠EFC=180°,∠BEF+∠EFD=180°,∠AEN=∠ENF,
∵EM平分∠BEF,FM平分∠EFD,EN平分∠AEF,
∴∠AEN=∠FEN,∠BEM=∠FEM,∠EFM=∠DFM,
∴∠BEM+∠MFD=90°,
∵∠AEF+∠BEF=180°,
∴∠AEN+∠BEM=90°,
则与∠BEM互余的角有∠AEN,∠NEF,∠ENF,∠EFM,∠MFD共5个,
故选B.
6.B
【解析】
解:∵△DEF是由△ABC通过平移得到,
∴BE=CF,
∴BE=(BF﹣EC),
∵BF=14,EC=6,
∴BE=(14﹣6)=4.
故选B.
7.B
【解析】
解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠CDB=90°,
∴∠A+∠ACD=90°,
∴与∠A互余的角有两个.
故选B.
8.C
【解析】
∵OP平分∠AOB,∴∠1=∠2,
∵MN∥OB,∴∠2=∠3,
所以补出来的部分应是:①、②.
故选C.
9.C
【解析】
由条件可知∠BAC=180° α,
∵AB∥CD,
∴β=∠BAC,
∴β=180° α,
故选C.
10.C
【解析】
解:过点E作EF∥AB,如图,∵AB∥CD,AB∥EF,∴CD∥EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∴∠FEA=β﹣γ,∴α+(β﹣γ)=180°,即α+β﹣γ=180°.
故选:C.
11.1150.
【解析】
如图,将各顶点标上字母,
∵△EFG是直角三角形,∴∠FEG=90°.
∵四边形ABCD是矩形,∴AD∥BC.
∵∠1=25°,
∴∠2=∠DEG=∠1+∠FEG=115°.
12.①③④⑤.
【解析】
①∵∠1=∠2,
∴a∥b,故此选项正确;
②∠3=∠6无法得出a∥b,故此选项错误;
③∵∠4+∠7=180°,
∴a∥b,故此选项正确;
④∵∠5+∠3=180°,
∴∠2+∠5=180°,
∴a∥b,故此选项正确;
⑤∵∠7=∠8,∠6=∠8,
∴∠6=∠7,
∴a∥b,故此选项正确;
综上所述,正确的有①③④⑤.
故答案为①③④⑤.
13.68°
【解析】
∵AD∥BC,∴∠DEF=∠EFG=56°,又根据对称可知∠DEF=∠FEG,∴∠AEG=180°-∠DEF-∠FEG=68°.
14.①②③
【解析】
①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
15. (3) (2) (1)
【解析】
解:观察图形,根据所给的信息可得:①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为(3);
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD的图形为(2);
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为(1).
故答案为:(3);(2);(1).
16..
【解析】
解答:
∵直尺的两边平行,
∴∠2=∠3;
∵∠3=∠4,∠1+∠2=90°,
∴∠1的余角有:∠2,∠3,∠4.
17.40°
【解析】
解:∵DE∥BC,∠AED=80°
∴∠ACB=∠AED=80°,∠EDC=∠BCD
∵CD平分∠ACB,
∴∠BCD=∠ACB=40°
∴∠EDC=40°
18.证明见解析.
【解析】
解:∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴∠A+∠B=180°,
∵CB⊥AB,
∴∠A=90°,
∴DA⊥AB.
考点:平行线的判定与性质.
19.(1);(2)证明见解析
【解析】
(1)解:∵
∴
∵
∴,
∵平分,
∴
∴;
(2)证明:∵
∴
∴
∵,
又∵
∴,
,
平分.
20.答案见解析
【解析】
解:如图:
(1)∠A+∠C+∠P=360;
(2)∠A+∠C=∠P;
(3)∠A+∠P=∠C;
(4)∠C+∠P=∠A.
说明理由(以第三个为例):
已知AB∥CD,根据两直线平行,同位角相等及三角形的一个外角等于两不相邻内角之和,可得∠C=∠A+∠P.
答案第1页,共2页
答案第2页,共7页
第二章 相交线与平行线单元测试卷(二)
一、单选题
1.下列说法正确的是( )
A.同位角相等 B.在同一平面内,如果⊥,⊥,则⊥
C.相等的角是对顶角 D.在同一平面内,如果∥,∥,则∥
2.如图,下列说法中错误的是( )
A.∠3与∠5是同位角 B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角 D.∠1和∠5是同位角
3.a、b、c是平面上的任意三条直线,它们的交点可以有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.以上都不正确
4.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm B.小于3cm
C.大于3cm D.大于或等于3cm
5.如图,AB∥CD,若EM平分∠BEF,FM平分∠EFD,EN平分∠AEF,则与∠BEM互余的角有( ).
A.6个 B.5个
C.4个 D.3个
6.如图,三角形DEF是由三角形ABC通过平移得到的,且点B,E,C,F在同一直线上.若BF=14,CE=6,则BE的长是( )
A.2 B.4 C.5 D.3
7.如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是( )
A.1 B.2 C.3 D.4
8.小颖在做下面的数学作业时,因钢笔漏墨水,不小心将部分字迹污损了,作业过程如下(涂黑部分即为污损部分):
如图,OP平分∠AOB,MN∥OB,试说明:OM=MN.理由:因为OP平分∠AOB,所以■,又因为MN∥OB,所以■,故∠1=∠3,所以OM=MN.小颖思考:污损部分应分别是以下四项中的两项:①∠1=∠2;②∠2=∠3;③∠3=∠4;④∠1=∠4.那么她补出来的部分应是( )
A.①④ B.②③
C.①② D.③④
9.如图所示,一辆汽车,经过两次转弯后,行驶的方向与原来保持平行,如果第一次转过的角度为α,第二次转过的角度为β,则β等于( )
A.α B.90°﹣α C.180°﹣α D.90°+α
10.如图,若AB∥CD,则α、β、γ之间的关系为( )
A.α+β+γ=360° B.α﹣β+γ=180°
C.α+β﹣γ=180° D.α+β+γ=180°
二、填空题
11.如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=___.
12.如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°;⑤∠6=∠8,其中能判断a∥b的是______(填序号)
13.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=56°,则∠AEG=_______.
14.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是________(填序号).
15.下列语句表示的图形是(只填序号)
①过点O的三条直线与另条一直线分别相交于点B、C、D三点:_____.
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD:_______.
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点:_________.
三、解答题
16.将直尺与三角尺按如图所示的方式叠放在一起.在图中标记的角中,写出所有与互余的角.
17.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
18.已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
19.如图,已知射线与直线交于点,平分,于,,且.
(1)求的度数;
(2)试说明平分.
20.如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.
试卷第1页,共3页
试卷第5页,共5页
参考答案:
1.D
【解析】
解:A选项只有在两直线平行时同位角相等,故A选项错误;
B选项在同一平面内,如果⊥,⊥,则,而不是⊥,故B选项错误;
C选项对顶角一定相等,但相等的角不一定是对顶角,故C选项错误;
D选项在同一平面内,如果∥,∥,则∥,故D选项正确.
故选:D.
2.D
【解析】
∠1和∠5不是同位角,D选项错误.
故选D.
3.B
【解析】
a、b、c是平面上的任意三条直线,①它们可以相交于1点,
②a∥b,b,c相交于一点,故它们的交点为2点,
③a、b、c两两相交于不同点,交点为3个,
④a∥b∥c,它们有0个交点,
故选B.
4.D
【解析】
试题解析:A到直线MN的距离是3cm,根据点到直线距离的定义,3cm表示垂线段的长度,根据垂线段最短,其它线段的长度大于或等于3cm,
故选D.
5.B
【解析】
∵AB∥CD,
∴∠AEF+∠EFC=180°,∠BEF+∠EFD=180°,∠AEN=∠ENF,
∵EM平分∠BEF,FM平分∠EFD,EN平分∠AEF,
∴∠AEN=∠FEN,∠BEM=∠FEM,∠EFM=∠DFM,
∴∠BEM+∠MFD=90°,
∵∠AEF+∠BEF=180°,
∴∠AEN+∠BEM=90°,
则与∠BEM互余的角有∠AEN,∠NEF,∠ENF,∠EFM,∠MFD共5个,
故选B.
6.B
【解析】
解:∵△DEF是由△ABC通过平移得到,
∴BE=CF,
∴BE=(BF﹣EC),
∵BF=14,EC=6,
∴BE=(14﹣6)=4.
故选B.
7.B
【解析】
解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠CDB=90°,
∴∠A+∠ACD=90°,
∴与∠A互余的角有两个.
故选B.
8.C
【解析】
∵OP平分∠AOB,∴∠1=∠2,
∵MN∥OB,∴∠2=∠3,
所以补出来的部分应是:①、②.
故选C.
9.C
【解析】
由条件可知∠BAC=180° α,
∵AB∥CD,
∴β=∠BAC,
∴β=180° α,
故选C.
10.C
【解析】
解:过点E作EF∥AB,如图,∵AB∥CD,AB∥EF,∴CD∥EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∴∠FEA=β﹣γ,∴α+(β﹣γ)=180°,即α+β﹣γ=180°.
故选:C.
11.1150.
【解析】
如图,将各顶点标上字母,
∵△EFG是直角三角形,∴∠FEG=90°.
∵四边形ABCD是矩形,∴AD∥BC.
∵∠1=25°,
∴∠2=∠DEG=∠1+∠FEG=115°.
12.①③④⑤.
【解析】
①∵∠1=∠2,
∴a∥b,故此选项正确;
②∠3=∠6无法得出a∥b,故此选项错误;
③∵∠4+∠7=180°,
∴a∥b,故此选项正确;
④∵∠5+∠3=180°,
∴∠2+∠5=180°,
∴a∥b,故此选项正确;
⑤∵∠7=∠8,∠6=∠8,
∴∠6=∠7,
∴a∥b,故此选项正确;
综上所述,正确的有①③④⑤.
故答案为①③④⑤.
13.68°
【解析】
∵AD∥BC,∴∠DEF=∠EFG=56°,又根据对称可知∠DEF=∠FEG,∴∠AEG=180°-∠DEF-∠FEG=68°.
14.①②③
【解析】
①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
15. (3) (2) (1)
【解析】
解:观察图形,根据所给的信息可得:①过点O的三条直线与另一条直线分别相交于点B、C、D三点的图形为(3);
②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD的图形为(2);
③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点的图形为(1).
故答案为:(3);(2);(1).
16..
【解析】
解答:
∵直尺的两边平行,
∴∠2=∠3;
∵∠3=∠4,∠1+∠2=90°,
∴∠1的余角有:∠2,∠3,∠4.
17.40°
【解析】
解:∵DE∥BC,∠AED=80°
∴∠ACB=∠AED=80°,∠EDC=∠BCD
∵CD平分∠ACB,
∴∠BCD=∠ACB=40°
∴∠EDC=40°
18.证明见解析.
【解析】
解:∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴∠A+∠B=180°,
∵CB⊥AB,
∴∠A=90°,
∴DA⊥AB.
考点:平行线的判定与性质.
19.(1);(2)证明见解析
【解析】
(1)解:∵
∴
∵
∴,
∵平分,
∴
∴;
(2)证明:∵
∴
∴
∵,
又∵
∴,
,
平分.
20.答案见解析
【解析】
解:如图:
(1)∠A+∠C+∠P=360;
(2)∠A+∠C=∠P;
(3)∠A+∠P=∠C;
(4)∠C+∠P=∠A.
说明理由(以第三个为例):
已知AB∥CD,根据两直线平行,同位角相等及三角形的一个外角等于两不相邻内角之和,可得∠C=∠A+∠P.
答案第1页,共2页
答案第2页,共7页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
