2021-2022学年高一下学期数学北师大版(2019)必修第二册4.2专题讲座:两角和差在解三角形中的应用课件(共38张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册4.2专题讲座:两角和差在解三角形中的应用课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 17:23:07 | ||
图片预览








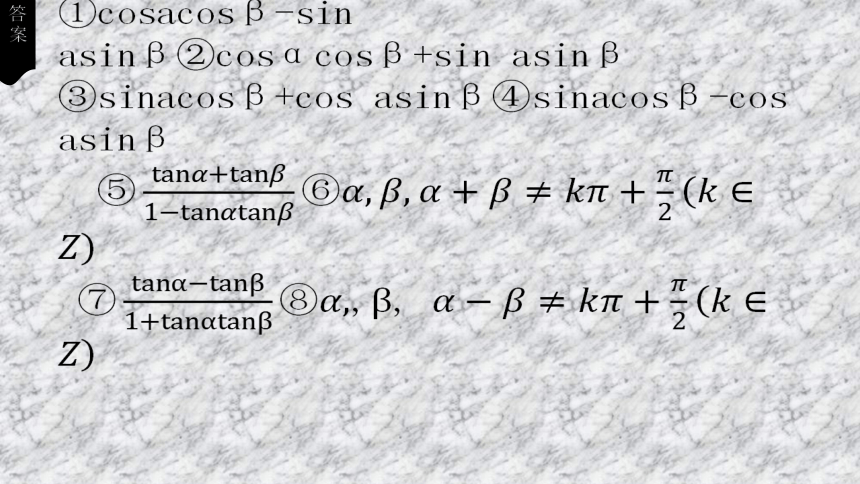

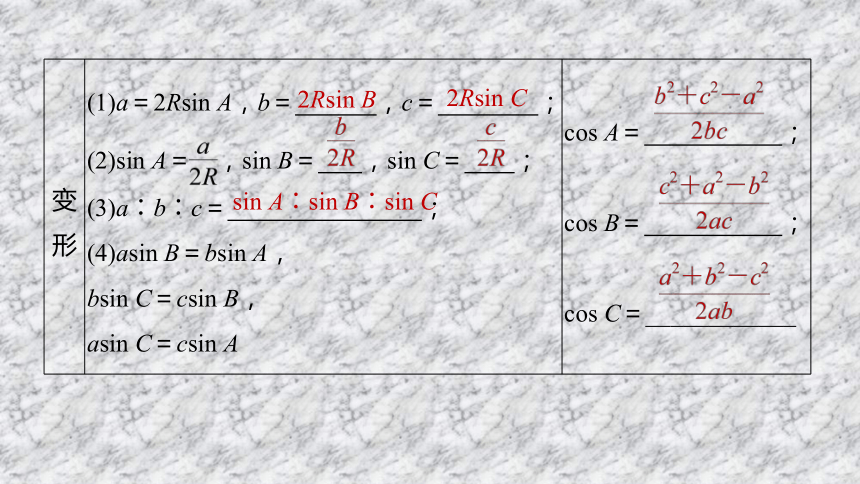

文档简介
(共38张PPT)
4.2 专题讲座:两角和差公式在解三角形中的应用
北师大(2019)必修2
基础知识梳理与理解
学以致用
题型分类 深度剖析
内容索引
基础知识梳理与理解
名称 公式 简记 使用条件
两角和 的余弦 公式 cos(α+β)=①_ Cα+β α,β∈R
两角差 的余弦 公式 cos(α-β)=②_ Ca-β α,β∈R
两角和 的正弦 公式 sin(α+β)=③_ Sa+β α,β∈R
两角差 的正弦 公式 sin(α-β)=④_ Sa-β
两角和 的正切 公式 tan(α+β)=⑤_ Tα+β ⑥
_
两角差 的正切 公式 tan(α-β)=⑦_ Ta-β ⑧_
知识点
1.两角和与差的三角函数公式
重
知识点
2.两角和与差的正切公式的变形
(1) tanα+tanβ=tan(α+β)(1-tanαtan β);
(2)tanα-tanβ =tan(α-β)(1+tanαtan β).
α
知识点
3.三角函数的叠加
asinα+bcosα=⑨__ sin(α+φ),其中
sinφ=⑩ _,cosφ=11__(a,b不同时为0).
重
知识点
4.积化和差与和差化积公式
(1)积化和差公式
知识点
4.积化和差与和差化积公式
(2)和差化积公式
①cosacosβ-sin asinβ②cosαcosβ+sin asinβ
③sinacosβ+cos asinβ④sinacosβ-cos asinβ
,β,
答案t
在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则
5.正弦定理、余弦定理
定理 正弦定理 余弦定理
内容 = = =2R a2= ;
b2= ;
c2=_______________
b2+c2-2bccos A
c2+a2-2cacos B
a2+b2-2abcos C
知识点
变形 (1)a=2Rsin A,b= ,c= ; (2)sin A= ,sin B= ,sin C= ; (3)a∶b∶c= ; (4)asin B=bsin A, bsin C=csin B, asin C=csin A cos A= ;
cos B= ;
cos C=____________
2Rsin B
2Rsin C
sin A∶sin B∶sin C
6.三角形常用面积公式
(1)S= a·ha(ha表示边a上的高);
(2)S= absin C= = ;
(3)S= r(a+b+c)(r为三角形内切圆半径).
acsin B
bcsin A
1.三角形内角和定理
在△ABC中,A+B+C=π;
知识拓展
2.三角形中的三角函数关系
(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C;
3.三角形中的射影定理
在△ABC中,a=bcos C+ccos B;b=acos C+ccos A;c=bcos A+acos B.
题型分类 深度剖析
第1 两角和差公式在解三角形中应用
第2 防错强化
两角和差公式在解三角形中应用
从②2bsinA=atan B,③(a-c) sin A+csin(A+B)=bsinB.这三个条件中任选一个,补充在下面的横线上,并加以解答.已知△ABC的内角A,B,C所对的边分别是a,b,c,若_.
(1)求角B;
(2)若a+c=4,求△ABC周长的最小值,并求出此时△ABC的面积.
典例
解(1)选①,由正弦定理得
因sinA≠0, 即
答
选②,由2bsinA=atanB,得
由正弦定理得
因sinA≠0,sinB=0,所以
答
选③,sin(A+B)=sin(π-C)=sinC,
由已知结合正弦定理可得
答
即3ac=16-b , 解得b≥2,当且仅当a=c=2时取等号,
周长的最小值为6,
此时△ABC的面积
方法总结
(1)由于三角形内角和为180°,因此解决三角形中的有关角时,要创设件,使之能运用两角和差公式;
(2)常用恒等式如下:
两角和差公式在解三角形中应用
△ABC的内角A,B,C的对边分别为a,b,c.已知B=150°
(1)若 求△ABC的面积;
(2)若 求C.
典例
分析
(1)已知角B和b,结合a,c的关系,由余弦定理建立关于c的方程,求解得出a,提示c,利用面积公式,即可得出结论;
(2)将A=30°-C代入已知等式,由两角差的正弦和辅助角公式,化简得出有关角C的三角函数值,结合C的范围,即可求解.
答
解(1)由余弦定理可得
△ABC的面积
(2);A+C=30°,.. sin
:0°两角和差公式在解三角形中应用
已知m=(cosA,sinA),n=(cos B,-sin B),若 且A,B,C为△ABC的三个内角,则C为()
典例
由题,在ABC中,m=(cos A,sin A),
即cosAcos B-sin AsinB
所以
答
两角和差公式在解三角形中应用
在△ABC中,若 B)=7, 则△ABC的面积为_.
典例
由B)=7得tanC=-7,sin C=-7cosC
则sinB=sin(A+C)=
由正弦定理得 得
得A △ABC的面积 4B·sinA
答
两角和差公式在解三角形中应用
这三个条件中任选一个,补充在下面的横线上,并解答问题.在△ABC中,内角A,B,C的对边分别为a,b,c,且满足_.
(1)求C;
(2)若△ABC的面积为10,D为AC的中点,求BD的最小值.
典例
方案1
解:选条件①. 可得
由正弦定理得 sin C.
B=π-(A+C),s in B=sin(A+C), sin Acos C+cos
故sin 4sinC,又sinA=0,the cosC,即
方案2
选条件②.
由正弦定理及同角三角函数
系式,得
;A+B+C=π, (B+C)=
又sinA≠0,
方案3
在△ABC中,由正弦定理得bsinC=csinB.
又
. sin
即
(2)由题意知 得ab=40.
由余弦定理得
当且仅当 且ab=40,即 时取等号,..BD的最小值为
防错强化
忽视三角形中角的限制条件致误
已知在△ABC中, 求cos C.
解 且 若 又 则 与A+B+C=π矛盾,
.。cosC=cos =-cos(A+B) =-cos Acos B+t
方法总结
若不注意三角形的内角和为π,即不认真讨论角的范围,就会多出一个解,本题也可以利用sinA学以致用
1.在中,内角所对的边分别是,已知,.
1.求;
2.若三角形的面积为,求角.
解析:1.由题意知, ,则,即有,
所以,由正弦定理, ,则;
2.因为三角形的面积为,、,
所以,则,①
由余弦定理得, ,②
由①②得, ,则,,
又,则即,解得
2.已知A、B、C为三角形ABC的三内角,其对应边分别为a、b、c、若有2acosC=2b+c成立.(1)求A的大小;
(2)若a=2,b+c=4,求三角形ABC的面积.
答案1)2acosC=2b+c.由正弦定理可知2sinAcosC=2sinB+sinC.①三角形中有:sinB=sin(A+C)=sinAcosC+cosAsinC,②
联立①②可化简得2cosAsinC+sinC=0.
在三角形中sinC-0.得 ,
(2)由余弦定理 得 即12=16-2bc+bc,解得bc=4
则
4.2 专题讲座:两角和差公式在解三角形中的应用
北师大(2019)必修2
基础知识梳理与理解
学以致用
题型分类 深度剖析
内容索引
基础知识梳理与理解
名称 公式 简记 使用条件
两角和 的余弦 公式 cos(α+β)=①_ Cα+β α,β∈R
两角差 的余弦 公式 cos(α-β)=②_ Ca-β α,β∈R
两角和 的正弦 公式 sin(α+β)=③_ Sa+β α,β∈R
两角差 的正弦 公式 sin(α-β)=④_ Sa-β
两角和 的正切 公式 tan(α+β)=⑤_ Tα+β ⑥
_
两角差 的正切 公式 tan(α-β)=⑦_ Ta-β ⑧_
知识点
1.两角和与差的三角函数公式
重
知识点
2.两角和与差的正切公式的变形
(1) tanα+tanβ=tan(α+β)(1-tanαtan β);
(2)tanα-tanβ =tan(α-β)(1+tanαtan β).
α
知识点
3.三角函数的叠加
asinα+bcosα=⑨__ sin(α+φ),其中
sinφ=⑩ _,cosφ=11__(a,b不同时为0).
重
知识点
4.积化和差与和差化积公式
(1)积化和差公式
知识点
4.积化和差与和差化积公式
(2)和差化积公式
①cosacosβ-sin asinβ②cosαcosβ+sin asinβ
③sinacosβ+cos asinβ④sinacosβ-cos asinβ
,β,
答案t
在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则
5.正弦定理、余弦定理
定理 正弦定理 余弦定理
内容 = = =2R a2= ;
b2= ;
c2=_______________
b2+c2-2bccos A
c2+a2-2cacos B
a2+b2-2abcos C
知识点
变形 (1)a=2Rsin A,b= ,c= ; (2)sin A= ,sin B= ,sin C= ; (3)a∶b∶c= ; (4)asin B=bsin A, bsin C=csin B, asin C=csin A cos A= ;
cos B= ;
cos C=____________
2Rsin B
2Rsin C
sin A∶sin B∶sin C
6.三角形常用面积公式
(1)S= a·ha(ha表示边a上的高);
(2)S= absin C= = ;
(3)S= r(a+b+c)(r为三角形内切圆半径).
acsin B
bcsin A
1.三角形内角和定理
在△ABC中,A+B+C=π;
知识拓展
2.三角形中的三角函数关系
(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C;
3.三角形中的射影定理
在△ABC中,a=bcos C+ccos B;b=acos C+ccos A;c=bcos A+acos B.
题型分类 深度剖析
第1 两角和差公式在解三角形中应用
第2 防错强化
两角和差公式在解三角形中应用
从②2bsinA=atan B,③(a-c) sin A+csin(A+B)=bsinB.这三个条件中任选一个,补充在下面的横线上,并加以解答.已知△ABC的内角A,B,C所对的边分别是a,b,c,若_.
(1)求角B;
(2)若a+c=4,求△ABC周长的最小值,并求出此时△ABC的面积.
典例
解(1)选①,由正弦定理得
因sinA≠0, 即
答
选②,由2bsinA=atanB,得
由正弦定理得
因sinA≠0,sinB=0,所以
答
选③,sin(A+B)=sin(π-C)=sinC,
由已知结合正弦定理可得
答
即3ac=16-b , 解得b≥2,当且仅当a=c=2时取等号,
周长的最小值为6,
此时△ABC的面积
方法总结
(1)由于三角形内角和为180°,因此解决三角形中的有关角时,要创设件,使之能运用两角和差公式;
(2)常用恒等式如下:
两角和差公式在解三角形中应用
△ABC的内角A,B,C的对边分别为a,b,c.已知B=150°
(1)若 求△ABC的面积;
(2)若 求C.
典例
分析
(1)已知角B和b,结合a,c的关系,由余弦定理建立关于c的方程,求解得出a,提示c,利用面积公式,即可得出结论;
(2)将A=30°-C代入已知等式,由两角差的正弦和辅助角公式,化简得出有关角C的三角函数值,结合C的范围,即可求解.
答
解(1)由余弦定理可得
△ABC的面积
(2);A+C=30°,.. sin
:0°
已知m=(cosA,sinA),n=(cos B,-sin B),若 且A,B,C为△ABC的三个内角,则C为()
典例
由题,在ABC中,m=(cos A,sin A),
即cosAcos B-sin AsinB
所以
答
两角和差公式在解三角形中应用
在△ABC中,若 B)=7, 则△ABC的面积为_.
典例
由B)=7得tanC=-7,sin C=-7cosC
则sinB=sin(A+C)=
由正弦定理得 得
得A △ABC的面积 4B·sinA
答
两角和差公式在解三角形中应用
这三个条件中任选一个,补充在下面的横线上,并解答问题.在△ABC中,内角A,B,C的对边分别为a,b,c,且满足_.
(1)求C;
(2)若△ABC的面积为10,D为AC的中点,求BD的最小值.
典例
方案1
解:选条件①. 可得
由正弦定理得 sin C.
B=π-(A+C),s in B=sin(A+C), sin Acos C+cos
故sin 4sinC,又sinA=0,the cosC,即
方案2
选条件②.
由正弦定理及同角三角函数
系式,得
;A+B+C=π, (B+C)=
又sinA≠0,
方案3
在△ABC中,由正弦定理得bsinC=csinB.
又
. sin
即
(2)由题意知 得ab=40.
由余弦定理得
当且仅当 且ab=40,即 时取等号,..BD的最小值为
防错强化
忽视三角形中角的限制条件致误
已知在△ABC中, 求cos C.
解 且 若 又 则 与A+B+C=π矛盾,
.。cosC=cos =-cos(A+B) =-cos Acos B+t
方法总结
若不注意三角形的内角和为π,即不认真讨论角的范围,就会多出一个解,本题也可以利用sinA
1.在中,内角所对的边分别是,已知,.
1.求;
2.若三角形的面积为,求角.
解析:1.由题意知, ,则,即有,
所以,由正弦定理, ,则;
2.因为三角形的面积为,、,
所以,则,①
由余弦定理得, ,②
由①②得, ,则,,
又,则即,解得
2.已知A、B、C为三角形ABC的三内角,其对应边分别为a、b、c、若有2acosC=2b+c成立.(1)求A的大小;
(2)若a=2,b+c=4,求三角形ABC的面积.
答案1)2acosC=2b+c.由正弦定理可知2sinAcosC=2sinB+sinC.①三角形中有:sinB=sin(A+C)=sinAcosC+cosAsinC,②
联立①②可化简得2cosAsinC+sinC=0.
在三角形中sinC-0.得 ,
(2)由余弦定理 得 即12=16-2bc+bc,解得bc=4
则
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
