5.2.1 平行线 同步习题课件 (含答案)
文档属性
| 名称 | 5.2.1 平行线 同步习题课件 (含答案) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 15:44:40 | ||
图片预览






文档简介
(共17张PPT)
第五章 相交线与平行线
5.2 平行线及其判定
5.2.1 平行线
下页
上页
在同一平面内,不重合的两条直线只有两种位
置关系:相交和平行
2.平行公理:
(1)经过直线外
点,有且只有
条
直线与这条直线平行
(2)如果两条直线都与第三条直线平行
那么这两条直线也互相平行
当堂训练
巩固基础
知识点1平行线的概念
在同一平面内,不重合的两条直线的位置关系
A.平行
B.垂直或平行
C.相交或平行
D.垂直或相交
下列说法正确的是
A.在同一平面内,没有公共点的两条线段
平行
B.两条不相交的直线是平行线
C.在同一平面内,没有公共点的两条射线
平
D.在同一平面内,没有公共点的两条直线
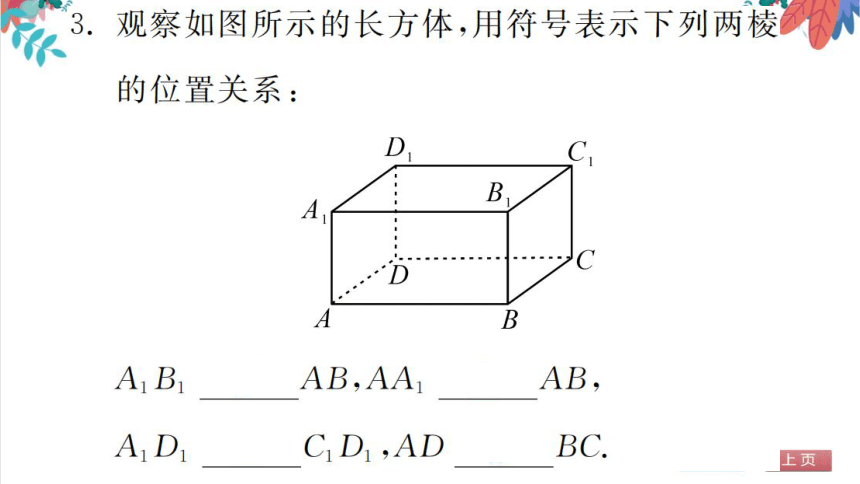
3.观察如图所示的长方体,用符号表示下列两棱
的位置关系:
B
A
C
A B
AB,AA1⊥AB,
A1D1⊥C1D1,AD∥BC
知识点2平行公理及其推论
4.下列说法正确的是
A.经过一点有一条直线与已知直线平彳
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线
平行
D.经过直线外一点有且只有一条直线与已知
直线平行
已知直线AB和一点P,过点P画直线与AB
平行,这样的直线可画
A.0条
B.1条
0条或1条
D.无数条
6.下列推理正确的是
A.因为a∥b,c∥d,所以b∥d
B.因为a∥C,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
B
N
E
B
(第7题图)
(第8题图)
根据要求作图
已知∠ABC,点P在AB上
(1)作直线PQ⊥BC,垂足为点Q;
(2)过点P作直线MN∥BC
C
M
B
下列生活实例:①交通道路上的斑马线;②天
上的彩虹;③百米跑道线;④一段平直的火车
铁轨线.其中属于平行线的有
A.1个
B.2个
个
D.4个
2.三条直线a,b,C,若a∥C,b∥c,则a与b的位
置关系是
B.a∥b
C.a⊥b或a∥b
D.无法确定
3.下列说法正确的有
①不相交的两条直线是平行线;②在同一平面
内,两条不重合的直线的位置关系有两种;
③若线段AB和CD没有交点,则AB∥CD;
④若a∥b,b∥c,则a∥C
A.1个
B.2个
D.4个
第五章 相交线与平行线
5.2 平行线及其判定
5.2.1 平行线
下页
上页
在同一平面内,不重合的两条直线只有两种位
置关系:相交和平行
2.平行公理:
(1)经过直线外
点,有且只有
条
直线与这条直线平行
(2)如果两条直线都与第三条直线平行
那么这两条直线也互相平行
当堂训练
巩固基础
知识点1平行线的概念
在同一平面内,不重合的两条直线的位置关系
A.平行
B.垂直或平行
C.相交或平行
D.垂直或相交
下列说法正确的是
A.在同一平面内,没有公共点的两条线段
平行
B.两条不相交的直线是平行线
C.在同一平面内,没有公共点的两条射线
平
D.在同一平面内,没有公共点的两条直线
3.观察如图所示的长方体,用符号表示下列两棱
的位置关系:
B
A
C
A B
AB,AA1⊥AB,
A1D1⊥C1D1,AD∥BC
知识点2平行公理及其推论
4.下列说法正确的是
A.经过一点有一条直线与已知直线平彳
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线
平行
D.经过直线外一点有且只有一条直线与已知
直线平行
已知直线AB和一点P,过点P画直线与AB
平行,这样的直线可画
A.0条
B.1条
0条或1条
D.无数条
6.下列推理正确的是
A.因为a∥b,c∥d,所以b∥d
B.因为a∥C,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
B
N
E
B
(第7题图)
(第8题图)
根据要求作图
已知∠ABC,点P在AB上
(1)作直线PQ⊥BC,垂足为点Q;
(2)过点P作直线MN∥BC
C
M
B
下列生活实例:①交通道路上的斑马线;②天
上的彩虹;③百米跑道线;④一段平直的火车
铁轨线.其中属于平行线的有
A.1个
B.2个
个
D.4个
2.三条直线a,b,C,若a∥C,b∥c,则a与b的位
置关系是
B.a∥b
C.a⊥b或a∥b
D.无法确定
3.下列说法正确的有
①不相交的两条直线是平行线;②在同一平面
内,两条不重合的直线的位置关系有两种;
③若线段AB和CD没有交点,则AB∥CD;
④若a∥b,b∥c,则a∥C
A.1个
B.2个
D.4个
