第五章 相交线与平行线 整理与复习 习题课件 (含答案)
文档属性
| 名称 | 第五章 相交线与平行线 整理与复习 习题课件 (含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 15:44:40 | ||
图片预览






文档简介
(共15张PPT)
第五章 整理与复习
下页
上页
知识梳理
在同一平面内,两条直线的位置关系是:相交
和平行
2.对顶角的性质:对顶角相等
3.垂线的性质:
(1)在同一平面内,过一点有且只有一条
直线与已知直线垂直
(2)垂线段最短
4.点到直线的距离:直线外一点到这条直线的
垂线段的长度,叫做点到直线的距离
“三线八角”中除对顶角和邻补角外,还有三类
角:同位角、内错角和同旁内角
6.平行公理及推论
(1)经过直线外一点,有且只有
条直线
与这条直线平行;
(2)平行于同一条直线的两条直线互相平行
平行线的判定方法
同位角相等,两直线平行
(2)内错角相等,两直线平行;
8.平行线的性质
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补
(1)命题:判断一件事情的语句,叫做
命题
(2)命题由题设和结论构成;
(3)命题分为真命题和假命题
经典例题
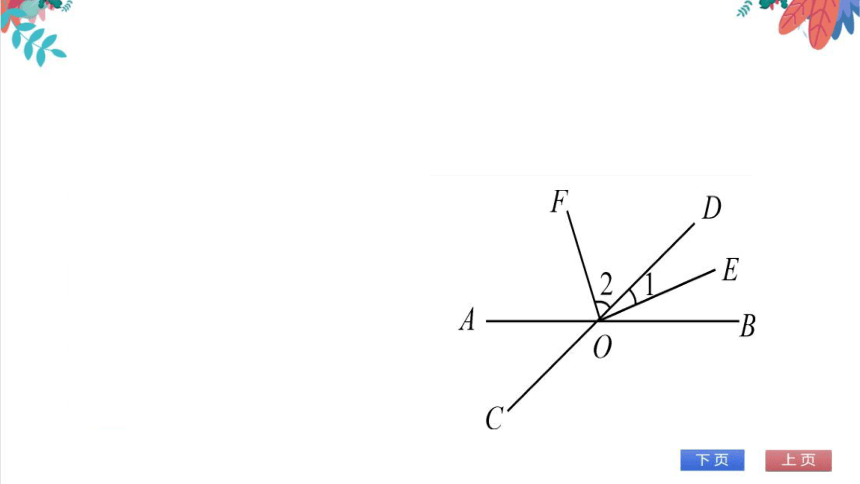
例1如图,已知直线AB与CD相交于点O,OE
平分∠BOD,OE⊥OF,且∠AOC=40°,求∠COF
的度数
【点拨】本题考查了对顶角、邻补角和垂直的定义
等知识,先从对顶角入手,求出∠BOD的度数,再
求出∠1=20°,进而∠2=900-20°=70°,最后利
用平角求出∠COF的度数
OE⊥OF,
∴∠EOF=90°
DEB
∠2=90°-20°=70
∴∠COF=180-70°=110
例2如图,点M,N,T和点P,Q,R分别在两条
直线上,且∠1
3,∠P=∠T.求证:
∠M=∠R
【点拨】本题综合考查了平行线的判定和平行线
的性质,先证出∠2=∠3,得PN∥QT,所以
∠PNM=∠T,进而∠PNM=∠P,因此PR∥
IT,故∠M=∠R
证明:∵∴∠1=∠2
∠1
∴∠2=∠3
PN∥QT
PNMT
人3
N
综合训练
如图,直线m与n相交于点O,若∠1+∠2
240°,则∠3的度数为
A.50°
B.60°
C.80
D.120
2
(第1题图)
4
2
(第4题图)
C
B
2
E
(第5题图
35
80°
(第6题图)
7.如图,直线l∥m,将含有45角的三角尺ABC
的直角顶点C放在直线m上,若∠1=20°,则
∠2的度数为25°
B
C
(第7题图)
(第8题图)
9.如图,在长方形ABCD中,AB=10cm,BC
6cm,将长方形ABCD沿着AB方向平移,若
使平移后的长方形与原来的长方形ABCD重
叠部分的面积为24cm2,则将长方形ABCD
沿着AB方向平移6cm
第五章 整理与复习
下页
上页
知识梳理
在同一平面内,两条直线的位置关系是:相交
和平行
2.对顶角的性质:对顶角相等
3.垂线的性质:
(1)在同一平面内,过一点有且只有一条
直线与已知直线垂直
(2)垂线段最短
4.点到直线的距离:直线外一点到这条直线的
垂线段的长度,叫做点到直线的距离
“三线八角”中除对顶角和邻补角外,还有三类
角:同位角、内错角和同旁内角
6.平行公理及推论
(1)经过直线外一点,有且只有
条直线
与这条直线平行;
(2)平行于同一条直线的两条直线互相平行
平行线的判定方法
同位角相等,两直线平行
(2)内错角相等,两直线平行;
8.平行线的性质
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补
(1)命题:判断一件事情的语句,叫做
命题
(2)命题由题设和结论构成;
(3)命题分为真命题和假命题
经典例题
例1如图,已知直线AB与CD相交于点O,OE
平分∠BOD,OE⊥OF,且∠AOC=40°,求∠COF
的度数
【点拨】本题考查了对顶角、邻补角和垂直的定义
等知识,先从对顶角入手,求出∠BOD的度数,再
求出∠1=20°,进而∠2=900-20°=70°,最后利
用平角求出∠COF的度数
OE⊥OF,
∴∠EOF=90°
DEB
∠2=90°-20°=70
∴∠COF=180-70°=110
例2如图,点M,N,T和点P,Q,R分别在两条
直线上,且∠1
3,∠P=∠T.求证:
∠M=∠R
【点拨】本题综合考查了平行线的判定和平行线
的性质,先证出∠2=∠3,得PN∥QT,所以
∠PNM=∠T,进而∠PNM=∠P,因此PR∥
IT,故∠M=∠R
证明:∵∴∠1=∠2
∠1
∴∠2=∠3
PN∥QT
PNMT
人3
N
综合训练
如图,直线m与n相交于点O,若∠1+∠2
240°,则∠3的度数为
A.50°
B.60°
C.80
D.120
2
(第1题图)
4
2
(第4题图)
C
B
2
E
(第5题图
35
80°
(第6题图)
7.如图,直线l∥m,将含有45角的三角尺ABC
的直角顶点C放在直线m上,若∠1=20°,则
∠2的度数为25°
B
C
(第7题图)
(第8题图)
9.如图,在长方形ABCD中,AB=10cm,BC
6cm,将长方形ABCD沿着AB方向平移,若
使平移后的长方形与原来的长方形ABCD重
叠部分的面积为24cm2,则将长方形ABCD
沿着AB方向平移6cm
