华东师大版八年级下册数学 19.2.1 菱形的性质(3)教案
文档属性
| 名称 | 华东师大版八年级下册数学 19.2.1 菱形的性质(3)教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 59.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览

文档简介
19.2.1菱形的性质
一、教学目标
1.知识与技能:经历菱形的性质的探究过程,掌握菱形的两条性质,并能灵活运用这些定理进行有关的论证和计算。
2.过程与方法:经历菱形的性质的探究过程,培养学生的动手实验、观察推理的意识,发展学生的形象思维和逻辑推理能力。
3.情感态度价值观:
从学生已有的知识出发,通过欣赏观察、动手操作、讨论交流、归纳总结,感受身边的数学,感受合作学习的成功,培养主动探求、勇于实践的精神,激发学习数学的激情,树立学好数学的信心。
二、教学重难点:
1.教学重点:掌握并运用菱形的性质。
2.教学难点:菱形性质的证明及灵活运用。
三、教学方法
问题情境——建立模型——解释应用——拓展巩固
四、教学过程
(一)折纸实验,引入课题
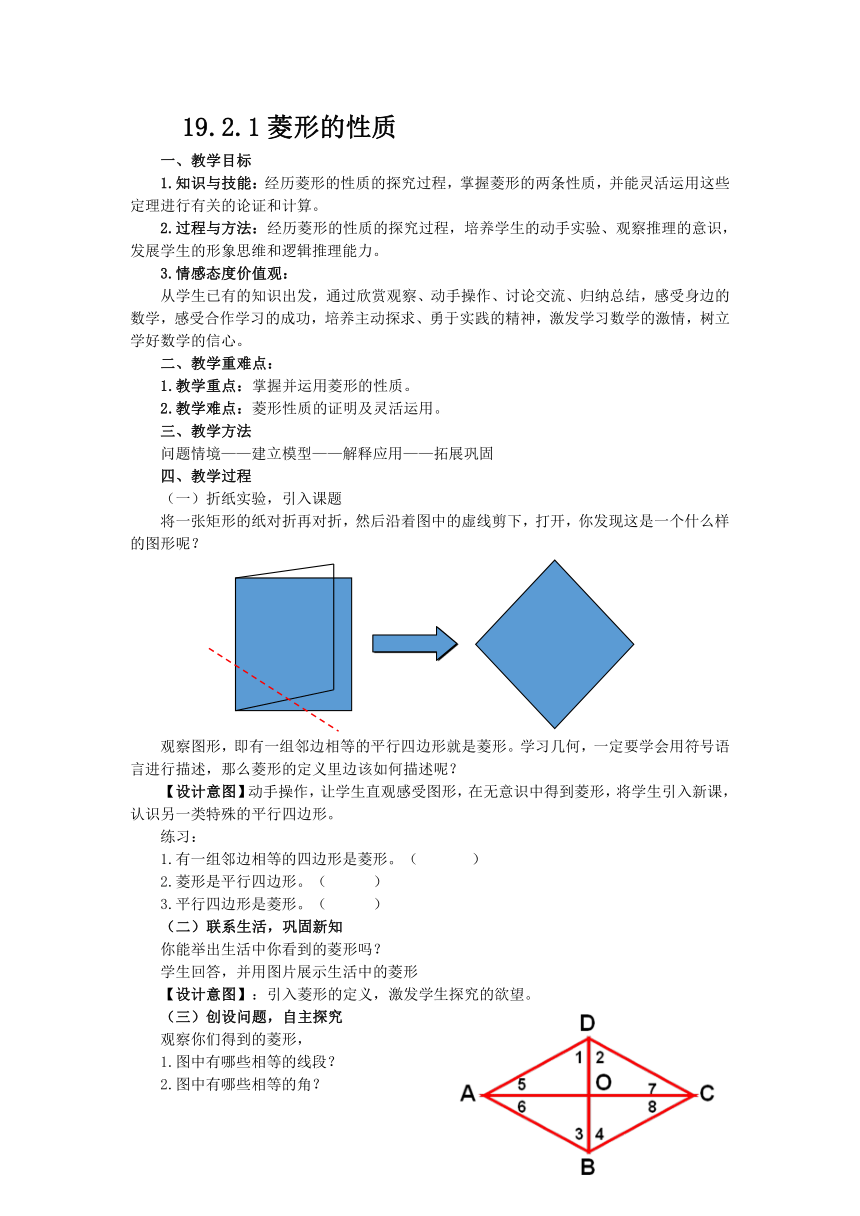
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
观察图形,即有一组邻边相等的平行四边形就是菱形。学习几何,一定要学会用符号语言进行描述,那么菱形的定义里边该如何描述呢?
【设计意图】动手操作,让学生直观感受图形,在无意识中得到菱形,将学生引入新课,认识另一类特殊的平行四边形。
练习:
1.有一组邻边相等的四边形是菱形。( )
2.菱形是平行四边形。( )
3.平行四边形是菱形。( )
(二)联系生活,巩固新知
你能举出生活中你看到的菱形吗?
学生回答,并用图片展示生活中的菱形
【设计意图】:引入菱形的定义,激发学生探究的欲望。
(三)创设问题,自主探究
观察你们得到的菱形,
1.图中有哪些相等的线段?
2.图中有哪些相等的角?
3.图中有哪些等腰三角形?
4.图中有哪些直角三角形?
5.菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
小组合作探究菱形的性质:它还有哪些特殊的性质,分别从它的边、角对角线入手,并完成下表:
对称性 边 角 对角线
平行四边形的一般性质 中心对称
菱形的特殊性质
总结得出菱形所具有的特殊性质:性质定理1:菱形的四条边都相等
性质定理2:菱形的对角线互相垂直
对于菱形的两条性质,如何用几何语言描述呢?请同学们认真思考。
【设计意图】:通过动手操作,合作交流,感受动手实验的乐趣,培养猜想的意识,感受直观操作得出猜想的便捷性,培养学生的观察、实验、猜想的推理能力。
(
A
D
C
B
)(四)证明性质,规范过程
我们通过折纸观察得出菱形的性质,那么如何证明它们呢?
已知:如图,四边形ABCD是菱形.
求证:(1)AB=BC=CD=AD;
(2)对角线 AC⊥BD。
【设计意图】通过对猜想的论证,进一步突出菱形性质的探索过程,体现了直观操作和逻辑推理的有机结合,进一步让学生感受到逻辑推理是得出结论的重要手段,很好地突出了教学的重点。
(五) 运用性质,讲解例题
学习了菱形的性质,那么如何运用并正确解题:
例:如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形。
(
B
A
D
C
)
(
A
D
C
B
第
3
题图
)【设计意图】将题型渗透到菱形的性质中,师生一起从整体分析问题,解决问题,并写出规范过程。
(六)题组训练,巩固新知
1.菱形具有而平行四边形不具有的性质是( )
(A)对角线互相平分 (B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直,每一条对角线平分一组对角线
2.已知菱形的周长是12cm,那么它的边长是_____。
3.菱形ABCD中∠BAD=60度,则∠ABD=_______。
【设计意图】:从简单的问题入手,运用菱形的性质解决问题,让学生在解题过程中掌握菱形的性质,达到“学数学,用数学”的目的,进一步培养学生解决问题的能力和推理论证的能力。
(七)归纳总结,构建新知
你有哪些收获?
1.菱形的定义:有一组邻边相等的平行四边形;
2.菱形的性质定理:
①菱形的四条边都相等
②菱形的对角线互相垂直
【设计意图】通过小结让学生理清本节课的知识结构,掌握菱形的两条性质,感受探究过程中的乐趣,体验克服困难的过程,树立自信心。
布置作业,拓展新知
题签
绘制平行四边形、矩形、菱形的思维导图。
五、板书设计
(
菱形的性质
)
对称性:轴对称
边:四条边都相等
定义 对角线:互相垂直
一组邻边相等 面积:S=底×高
=对角线乘积的一半
一、教学目标
1.知识与技能:经历菱形的性质的探究过程,掌握菱形的两条性质,并能灵活运用这些定理进行有关的论证和计算。
2.过程与方法:经历菱形的性质的探究过程,培养学生的动手实验、观察推理的意识,发展学生的形象思维和逻辑推理能力。
3.情感态度价值观:
从学生已有的知识出发,通过欣赏观察、动手操作、讨论交流、归纳总结,感受身边的数学,感受合作学习的成功,培养主动探求、勇于实践的精神,激发学习数学的激情,树立学好数学的信心。
二、教学重难点:
1.教学重点:掌握并运用菱形的性质。
2.教学难点:菱形性质的证明及灵活运用。
三、教学方法
问题情境——建立模型——解释应用——拓展巩固
四、教学过程
(一)折纸实验,引入课题
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
观察图形,即有一组邻边相等的平行四边形就是菱形。学习几何,一定要学会用符号语言进行描述,那么菱形的定义里边该如何描述呢?
【设计意图】动手操作,让学生直观感受图形,在无意识中得到菱形,将学生引入新课,认识另一类特殊的平行四边形。
练习:
1.有一组邻边相等的四边形是菱形。( )
2.菱形是平行四边形。( )
3.平行四边形是菱形。( )
(二)联系生活,巩固新知
你能举出生活中你看到的菱形吗?
学生回答,并用图片展示生活中的菱形
【设计意图】:引入菱形的定义,激发学生探究的欲望。
(三)创设问题,自主探究
观察你们得到的菱形,
1.图中有哪些相等的线段?
2.图中有哪些相等的角?
3.图中有哪些等腰三角形?
4.图中有哪些直角三角形?
5.菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
小组合作探究菱形的性质:它还有哪些特殊的性质,分别从它的边、角对角线入手,并完成下表:
对称性 边 角 对角线
平行四边形的一般性质 中心对称
菱形的特殊性质
总结得出菱形所具有的特殊性质:性质定理1:菱形的四条边都相等
性质定理2:菱形的对角线互相垂直
对于菱形的两条性质,如何用几何语言描述呢?请同学们认真思考。
【设计意图】:通过动手操作,合作交流,感受动手实验的乐趣,培养猜想的意识,感受直观操作得出猜想的便捷性,培养学生的观察、实验、猜想的推理能力。
(
A
D
C
B
)(四)证明性质,规范过程
我们通过折纸观察得出菱形的性质,那么如何证明它们呢?
已知:如图,四边形ABCD是菱形.
求证:(1)AB=BC=CD=AD;
(2)对角线 AC⊥BD。
【设计意图】通过对猜想的论证,进一步突出菱形性质的探索过程,体现了直观操作和逻辑推理的有机结合,进一步让学生感受到逻辑推理是得出结论的重要手段,很好地突出了教学的重点。
(五) 运用性质,讲解例题
学习了菱形的性质,那么如何运用并正确解题:
例:如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形。
(
B
A
D
C
)
(
A
D
C
B
第
3
题图
)【设计意图】将题型渗透到菱形的性质中,师生一起从整体分析问题,解决问题,并写出规范过程。
(六)题组训练,巩固新知
1.菱形具有而平行四边形不具有的性质是( )
(A)对角线互相平分 (B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直,每一条对角线平分一组对角线
2.已知菱形的周长是12cm,那么它的边长是_____。
3.菱形ABCD中∠BAD=60度,则∠ABD=_______。
【设计意图】:从简单的问题入手,运用菱形的性质解决问题,让学生在解题过程中掌握菱形的性质,达到“学数学,用数学”的目的,进一步培养学生解决问题的能力和推理论证的能力。
(七)归纳总结,构建新知
你有哪些收获?
1.菱形的定义:有一组邻边相等的平行四边形;
2.菱形的性质定理:
①菱形的四条边都相等
②菱形的对角线互相垂直
【设计意图】通过小结让学生理清本节课的知识结构,掌握菱形的两条性质,感受探究过程中的乐趣,体验克服困难的过程,树立自信心。
布置作业,拓展新知
题签
绘制平行四边形、矩形、菱形的思维导图。
五、板书设计
(
菱形的性质
)
对称性:轴对称
边:四条边都相等
定义 对角线:互相垂直
一组邻边相等 面积:S=底×高
=对角线乘积的一半
