华师大版>八年级下册第18章 平行四边形复习课 课件(共21张PPT)
文档属性
| 名称 | 华师大版>八年级下册第18章 平行四边形复习课 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 883.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 16:56:20 | ||
图片预览



文档简介
(共21张PPT)
四边形
没有对边平行的四边形
梯形
平行四边形
矩形
菱形
直角梯形
等腰梯形
复 习 目 标
我要学会:1、平行四边形及特殊平行四边 形的定义和性质
2、会利用性质解决实际问题
复 习 重 难 点
我要争取突破的困难:平行四边形,矩形, 菱形,正方形,梯形性质应用
模块1复习目标
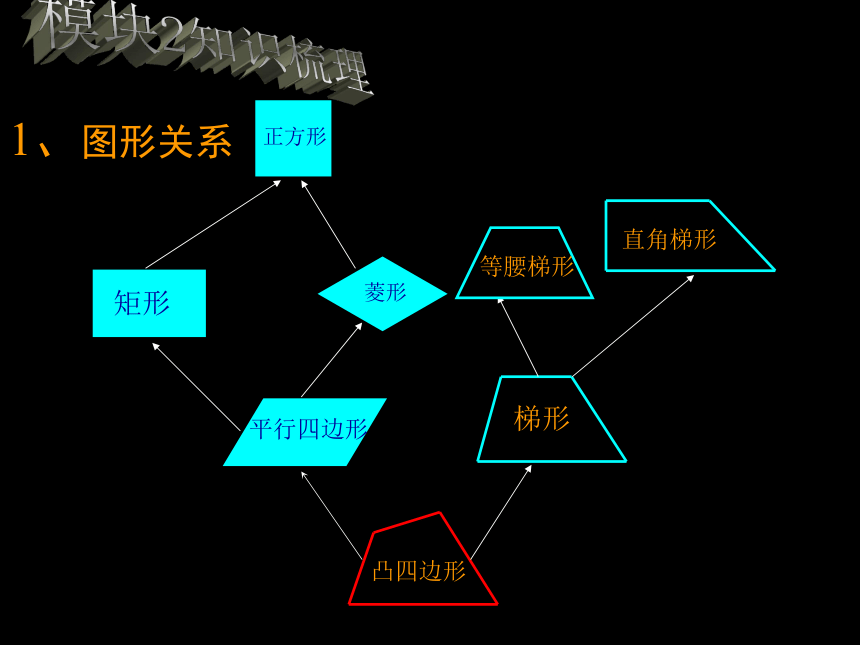
凸四边形
平行四边形
矩形
菱形
正方形
梯形
等腰梯形
直角梯形
1、图形关系
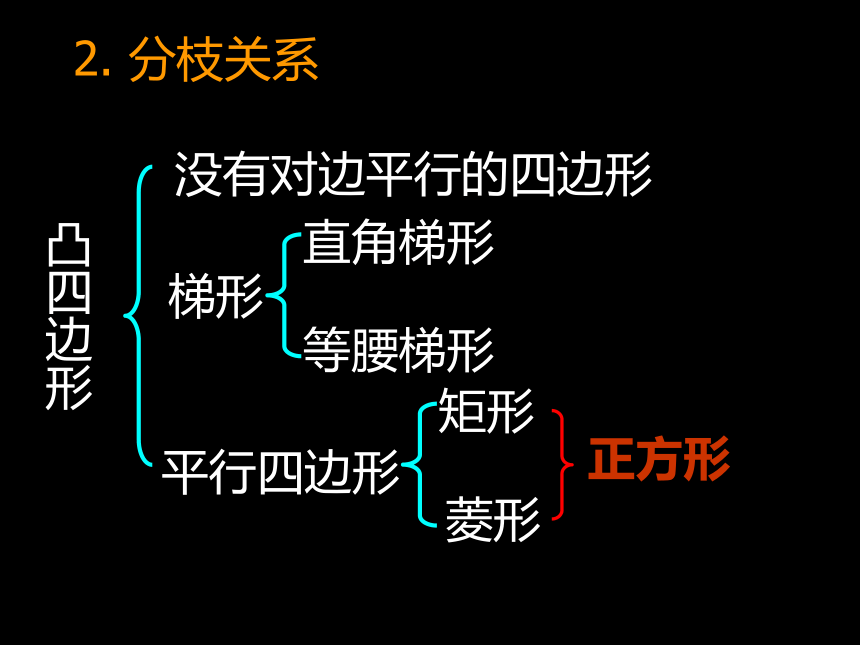
2. 分枝关系
凸四边形
没有对边平行的四边形
梯形
平行四边形
矩形
菱形
直角梯形
等腰梯形
正方形
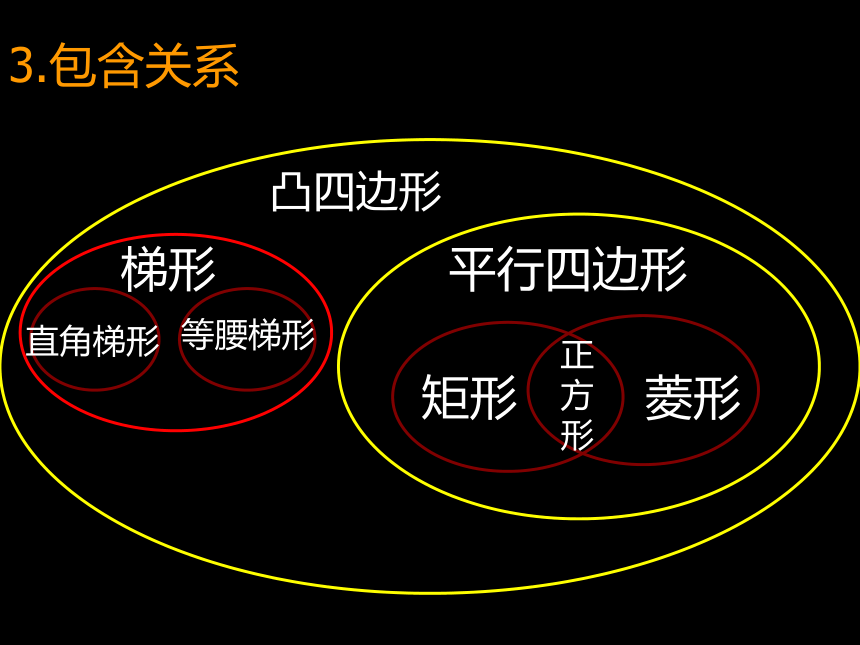
3.包含关系
凸四边形
平行四边形
矩形
菱形
梯形
直角梯形
等腰梯形
正方形
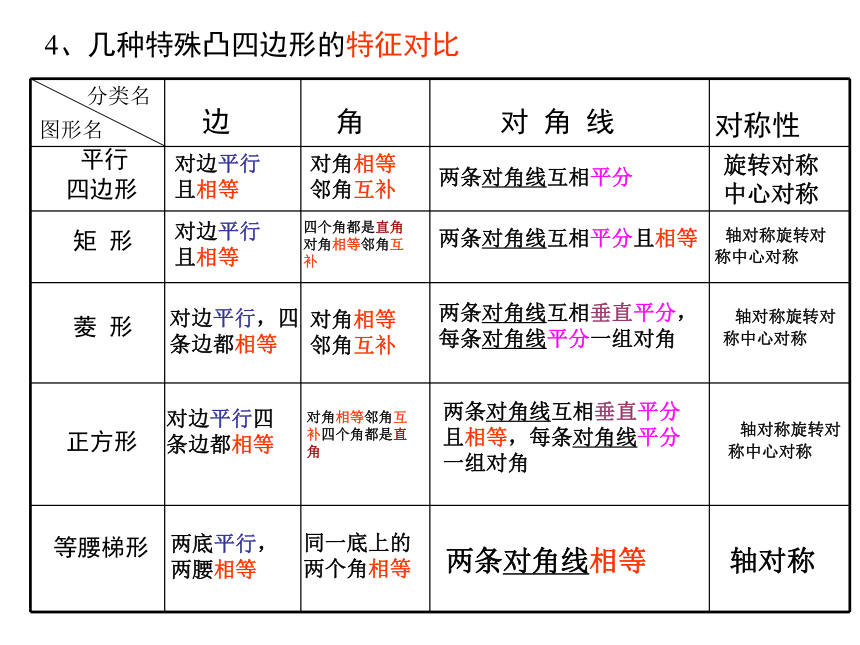
4、几种特殊凸四边形的特征对比
平行
四边形
矩 形
菱 形
正方形
等腰梯形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行四条边都相等
两底平行,
两腰相等
角
对角相等邻角互补
四个角都是直角对角相等邻角互补
对角相等邻角互补
对角相等邻角互补四个角都是直角
同一底上的
两个角相等
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
两条对角线相等
对称性
旋转对称中心对称
轴对称旋转对称中心对称
轴对称旋转对称中心对称
轴对称旋转对称中心对称
轴对称
分类名
图形名
例1 从平行四边形的一个钝角顶点引分两边的垂线,
如果这两条垂线间的夹角为75°,求这平行四边形各
内角的度数.
F
E
D
C
B
A
解:由题意得
∵∠EAF= 75°
∴∠C = ∠BAD= 105°
∠B= ∠D= 75°
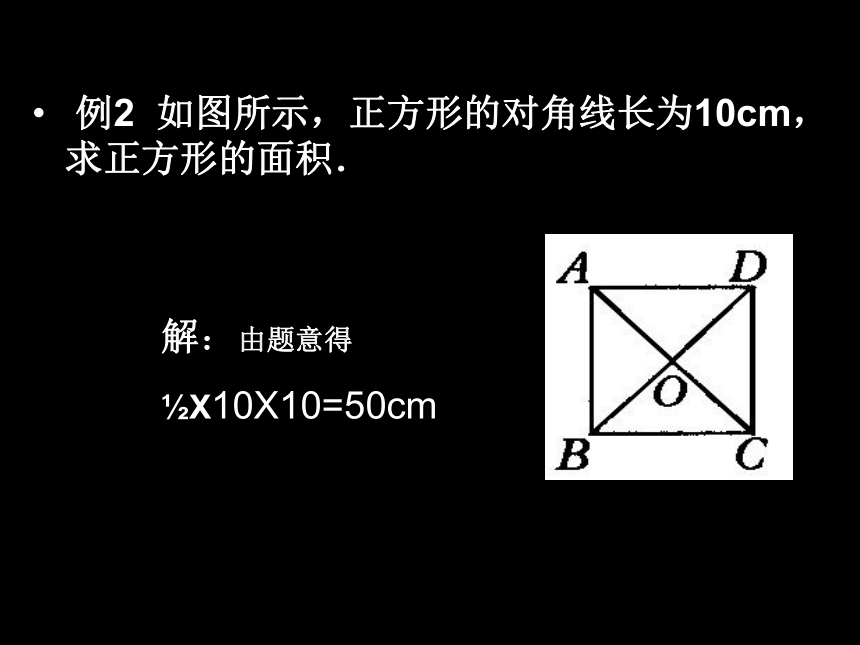
例2 如图所示,正方形的对角线长为10cm,求正方形的面积.
解:由题意得
X10X10=50cm
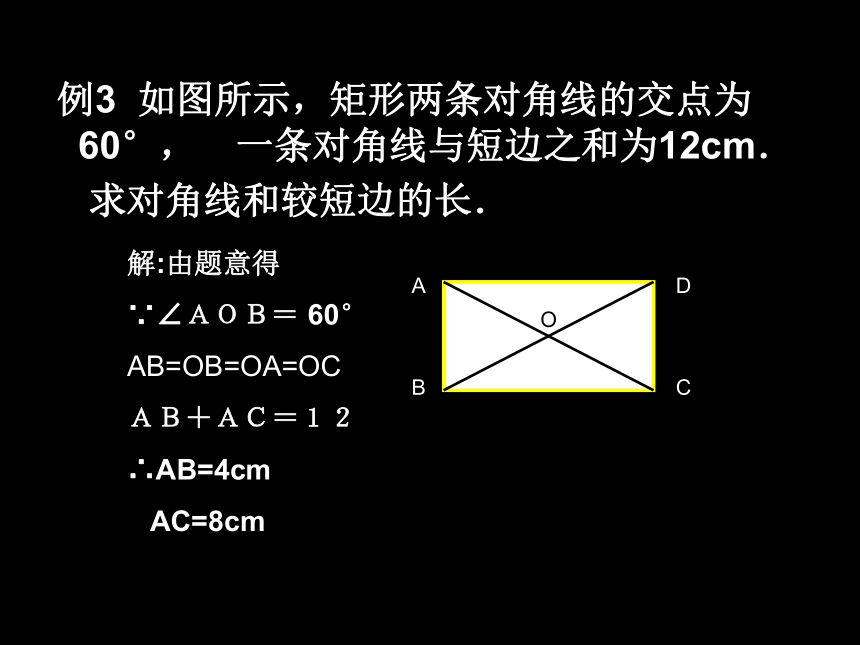
例3 如图所示,矩形两条对角线的交点为60°,一条对角线与短边之和为12cm.
求对角线和较短边的长.
A
B
C
D
O
解:由题意得
∵∠AOB= 60°
AB=OB=OA=OC
AB+AC=12
∴AB=4cm
AC=8cm
例题4
如图所示,在梯形ABCD中,AD∥BC,且AB=AD+BC,M为DC的中点,说明AM⊥BM。
A
C
B
D
M
温馨提示
把ΔADM绕点M旋转180°ΔABE是等腰三角形
A
C
B
D
E
M
解:由题意得
∵ΔADM≌ΔABE
AD=CE,AM=ME
∴AB=BC+AD=BC+CE=BE
M又为AE中点,
AM⊥BM(三线合一)
(一)判断题:
1.平行四边形的对角线相等; ( )
2.对角线互相垂直的四边形菱形; ( )
3.有两个角相等的梯形是等腰梯形; ( )
4.菱形的对角线互相垂直平分,且平分所在内角;( )
5.对角线相等的四边形是矩形; ( )
6.正方形既是矩形也是菱形;( )
(二)选择题:
1.正方形具有而菱形不一定具有的性质是( )。
(A)对角线互相平分。 (B)对角线相等。
(C)对角线平分一组对角。 (D)对角线互相垂直。
B
2.顺次连结四边形各边中点所得到的四边形一定是( )
(A)矩形。 (B)正方形。(C ) 菱形。(D)平行四边形
D
3.内角和等于外角和的多边形是( )
(A) 三角形。(B)四边形。(C )五边形。(D)六边形。
B
4.下列性质中,平行四边形不一定具备的是( )
(A)对角相等。(B)邻角互补。(C )对角互补。(D)内角和是360°。
C
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)等边三角形。(B)平行四边形。(C )菱形。(D)等腰梯形。
C
D
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C )
(D)
.
用一条直线将下图分为面积相等的两部份。
如有雷同,纯属巧合
如图,在直角梯形ABCD中,AD//BC, ,AB=8cm,AD=24cm,BC=27cm. 动点P从点A开始沿AD边以1cm/s的速度运动;动点Q从点C开始沿CB边以3cm/s的速度运动。现点P,点Q分别从点A,点C同时出发,当其中一点到达端点时,另一点也随之停止运动。设运动时间为t秒。求:
(1)t为何值时,四边形PQCD为平行四边形;
(2) t为何值时,四边形PQCD为平等腰梯形;
(3)在运动过程中,P、Q、B、A四点能构成矩形和正方形吗?请说明理由。
Q
P
D
A
C
B
P
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
P
Q
P
P
P
Q
Q
Q
解:由题意得,(0≤t≤9)
AP= t,CQ=3 t
E
F
①PD=CQ
24- t=3 t, t=6
②QE=FC=3
3 t-6= 24-t, t=7.5
③AP=BQ
t=27-3 t, t=6.75
④AP=BQ=AB=6.75
因为AB=8所以不成立
四边形
没有对边平行的四边形
梯形
平行四边形
矩形
菱形
直角梯形
等腰梯形
.
.
如图所示,正方形ABCD的边长为1,AB,AD上各有一点P、Q,如果ΔAPQ的周长为2,求∠PCQ的度数
提示把ΔCDQ绕点C逆时针旋转90°
D
C
A
B
E
Q
P
三角形的中位线——连结三角形任意两边中点的线段叫做三角形的中位线。如图DE DF EF就是中位线三角形的中位线定理:三角形的中位线平行于对边,且等于它的一半,例如DE╩ BC
请解答----连接任意四边请形的四边中点
得到的四边形为平行四边形
D
B
E
C
A
F
A
B
C
D
E
F
H
G
证明:由题意得
∵EF‖AC ‖HG
∴ EF‖HG
∵ EH‖BD ‖FG
∴ EH‖FG
所以四边形EFGH为平行四边形
四边形
没有对边平行的四边形
梯形
平行四边形
矩形
菱形
直角梯形
等腰梯形
复 习 目 标
我要学会:1、平行四边形及特殊平行四边 形的定义和性质
2、会利用性质解决实际问题
复 习 重 难 点
我要争取突破的困难:平行四边形,矩形, 菱形,正方形,梯形性质应用
模块1复习目标
凸四边形
平行四边形
矩形
菱形
正方形
梯形
等腰梯形
直角梯形
1、图形关系
2. 分枝关系
凸四边形
没有对边平行的四边形
梯形
平行四边形
矩形
菱形
直角梯形
等腰梯形
正方形
3.包含关系
凸四边形
平行四边形
矩形
菱形
梯形
直角梯形
等腰梯形
正方形
4、几种特殊凸四边形的特征对比
平行
四边形
矩 形
菱 形
正方形
等腰梯形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行四条边都相等
两底平行,
两腰相等
角
对角相等邻角互补
四个角都是直角对角相等邻角互补
对角相等邻角互补
对角相等邻角互补四个角都是直角
同一底上的
两个角相等
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
两条对角线相等
对称性
旋转对称中心对称
轴对称旋转对称中心对称
轴对称旋转对称中心对称
轴对称旋转对称中心对称
轴对称
分类名
图形名
例1 从平行四边形的一个钝角顶点引分两边的垂线,
如果这两条垂线间的夹角为75°,求这平行四边形各
内角的度数.
F
E
D
C
B
A
解:由题意得
∵∠EAF= 75°
∴∠C = ∠BAD= 105°
∠B= ∠D= 75°
例2 如图所示,正方形的对角线长为10cm,求正方形的面积.
解:由题意得
X10X10=50cm
例3 如图所示,矩形两条对角线的交点为60°,一条对角线与短边之和为12cm.
求对角线和较短边的长.
A
B
C
D
O
解:由题意得
∵∠AOB= 60°
AB=OB=OA=OC
AB+AC=12
∴AB=4cm
AC=8cm
例题4
如图所示,在梯形ABCD中,AD∥BC,且AB=AD+BC,M为DC的中点,说明AM⊥BM。
A
C
B
D
M
温馨提示
把ΔADM绕点M旋转180°ΔABE是等腰三角形
A
C
B
D
E
M
解:由题意得
∵ΔADM≌ΔABE
AD=CE,AM=ME
∴AB=BC+AD=BC+CE=BE
M又为AE中点,
AM⊥BM(三线合一)
(一)判断题:
1.平行四边形的对角线相等; ( )
2.对角线互相垂直的四边形菱形; ( )
3.有两个角相等的梯形是等腰梯形; ( )
4.菱形的对角线互相垂直平分,且平分所在内角;( )
5.对角线相等的四边形是矩形; ( )
6.正方形既是矩形也是菱形;( )
(二)选择题:
1.正方形具有而菱形不一定具有的性质是( )。
(A)对角线互相平分。 (B)对角线相等。
(C)对角线平分一组对角。 (D)对角线互相垂直。
B
2.顺次连结四边形各边中点所得到的四边形一定是( )
(A)矩形。 (B)正方形。(C ) 菱形。(D)平行四边形
D
3.内角和等于外角和的多边形是( )
(A) 三角形。(B)四边形。(C )五边形。(D)六边形。
B
4.下列性质中,平行四边形不一定具备的是( )
(A)对角相等。(B)邻角互补。(C )对角互补。(D)内角和是360°。
C
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)等边三角形。(B)平行四边形。(C )菱形。(D)等腰梯形。
C
D
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C )
(D)
.
用一条直线将下图分为面积相等的两部份。
如有雷同,纯属巧合
如图,在直角梯形ABCD中,AD//BC, ,AB=8cm,AD=24cm,BC=27cm. 动点P从点A开始沿AD边以1cm/s的速度运动;动点Q从点C开始沿CB边以3cm/s的速度运动。现点P,点Q分别从点A,点C同时出发,当其中一点到达端点时,另一点也随之停止运动。设运动时间为t秒。求:
(1)t为何值时,四边形PQCD为平行四边形;
(2) t为何值时,四边形PQCD为平等腰梯形;
(3)在运动过程中,P、Q、B、A四点能构成矩形和正方形吗?请说明理由。
Q
P
D
A
C
B
P
D
A
C
B
D
A
C
B
D
A
C
B
D
A
C
B
P
Q
P
P
P
Q
Q
Q
解:由题意得,(0≤t≤9)
AP= t,CQ=3 t
E
F
①PD=CQ
24- t=3 t, t=6
②QE=FC=3
3 t-6= 24-t, t=7.5
③AP=BQ
t=27-3 t, t=6.75
④AP=BQ=AB=6.75
因为AB=8所以不成立
四边形
没有对边平行的四边形
梯形
平行四边形
矩形
菱形
直角梯形
等腰梯形
.
.
如图所示,正方形ABCD的边长为1,AB,AD上各有一点P、Q,如果ΔAPQ的周长为2,求∠PCQ的度数
提示把ΔCDQ绕点C逆时针旋转90°
D
C
A
B
E
Q
P
三角形的中位线——连结三角形任意两边中点的线段叫做三角形的中位线。如图DE DF EF就是中位线三角形的中位线定理:三角形的中位线平行于对边,且等于它的一半,例如DE╩ BC
请解答----连接任意四边请形的四边中点
得到的四边形为平行四边形
D
B
E
C
A
F
A
B
C
D
E
F
H
G
证明:由题意得
∵EF‖AC ‖HG
∴ EF‖HG
∵ EH‖BD ‖FG
∴ EH‖FG
所以四边形EFGH为平行四边形
