华东师大版八年级下册数学 19.2 菱形 课件(共21张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.2 菱形 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 17:30:06 | ||
图片预览








文档简介
(共21张PPT)
19.2 菱形
知识回顾
平行四边形的对边平行且相等;
平行线之间的距离处处相等
平行四边形的概念及性质
平行四边形的对角相等、邻角互补;
平行四边形的对角线互相平分 ;
平行四边形是中心对称图形 .
平行四边形:
两组对边分别平行的是四边形是平行四边形。
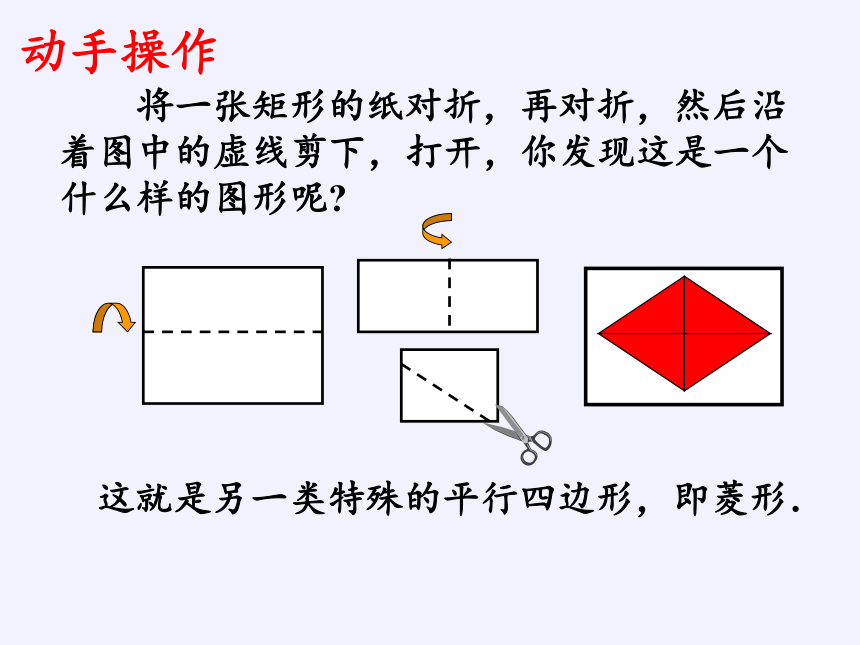
将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢
动手操作
这就是另一类特殊的平行四边形,即菱形.
19.2 菱形
一、菱形的性质
感受
生活
三菱汽车
美观别致的“菱形”
一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形,它具有一些特殊的性质.
菱形的特殊性质:
1)菱形的四条边都相等。
菱形的性质
2)菱形的对角线互相垂直。(平分所在对角)
性质定理1:菱形的四条边都相等。
已知:如图,在菱形ABCD中,AB=BC.
求证:AB=BC=CD=DA
分组讨论并证明
性质定理2:菱形的对角线互相垂直。
已知:如图,在菱形ABCD中,AB=BC,求证:AC⊥BD
。
A
B
C
D
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗
菱形
A
B
C
D
O
E
S菱形=BC×AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗
S菱形=底×高=对角线乘积的一半
补充知识:菱形的面积
ABCD=4S△AOB= 4* (OA ×OB)= (AC×BD)
S菱形
合情推理
A
B
C
D
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形。
(1)在菱形ABCD中,
∠B+∠BAD=180 (两直线平行同旁内角互补)
又∵∠BAD=2∠B,
∴∠B=60 .
(2)在菱形ABCD中,
解:
AB=BC(菱形的四条边都相等)
∴在△ABC中,∠BAC=∠BCA(等边对等角)
又∵∠B+∠BAC+∠BCA=180 (三角形内角和公式)
∴∠BAC=∠BCA=∠B=60
∴AB=BC=AC(等角对等边)
即ABC是等边三角形.
AD∥BC,
学以致用
1.已知菱形的周长是12cm,那么它的边长是______.
3cm
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
想一想
2.菱形的两条对角线的长分别为6cm和8cm,那么菱形的面积是_____.
24cm2
巩固练习
1.菱形的两条对角线长分别是6cm和8cm,则菱形的周长______,面积_________。
2.已知菱形的两个邻角的比是1:5,高是8cm,则菱形的周长为______。
这
节课
你
学
到
了
什
么?
回味无穷
从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形是中心对称图形,也是轴对称图形;
③菱形的四边都相等;
④菱形的对角线互相垂直。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
请同学们将关于菱形的定义、性质,对称性面积计算课后填入我们的知识总结表。
ab.
你能探究吗?
请把有一个内角为72°的菱形
分成4个等腰三角形。
)72°
谢 谢
19.2 菱形
知识回顾
平行四边形的对边平行且相等;
平行线之间的距离处处相等
平行四边形的概念及性质
平行四边形的对角相等、邻角互补;
平行四边形的对角线互相平分 ;
平行四边形是中心对称图形 .
平行四边形:
两组对边分别平行的是四边形是平行四边形。
将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢
动手操作
这就是另一类特殊的平行四边形,即菱形.
19.2 菱形
一、菱形的性质
感受
生活
三菱汽车
美观别致的“菱形”
一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形,它具有一些特殊的性质.
菱形的特殊性质:
1)菱形的四条边都相等。
菱形的性质
2)菱形的对角线互相垂直。(平分所在对角)
性质定理1:菱形的四条边都相等。
已知:如图,在菱形ABCD中,AB=BC.
求证:AB=BC=CD=DA
分组讨论并证明
性质定理2:菱形的对角线互相垂直。
已知:如图,在菱形ABCD中,AB=BC,求证:AC⊥BD
。
A
B
C
D
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗
菱形
A
B
C
D
O
E
S菱形=BC×AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗
S菱形=底×高=对角线乘积的一半
补充知识:菱形的面积
ABCD=4S△AOB= 4* (OA ×OB)= (AC×BD)
S菱形
合情推理
A
B
C
D
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形。
(1)在菱形ABCD中,
∠B+∠BAD=180 (两直线平行同旁内角互补)
又∵∠BAD=2∠B,
∴∠B=60 .
(2)在菱形ABCD中,
解:
AB=BC(菱形的四条边都相等)
∴在△ABC中,∠BAC=∠BCA(等边对等角)
又∵∠B+∠BAC+∠BCA=180 (三角形内角和公式)
∴∠BAC=∠BCA=∠B=60
∴AB=BC=AC(等角对等边)
即ABC是等边三角形.
AD∥BC,
学以致用
1.已知菱形的周长是12cm,那么它的边长是______.
3cm
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
想一想
2.菱形的两条对角线的长分别为6cm和8cm,那么菱形的面积是_____.
24cm2
巩固练习
1.菱形的两条对角线长分别是6cm和8cm,则菱形的周长______,面积_________。
2.已知菱形的两个邻角的比是1:5,高是8cm,则菱形的周长为______。
这
节课
你
学
到
了
什
么?
回味无穷
从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形是中心对称图形,也是轴对称图形;
③菱形的四边都相等;
④菱形的对角线互相垂直。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
请同学们将关于菱形的定义、性质,对称性面积计算课后填入我们的知识总结表。
ab.
你能探究吗?
请把有一个内角为72°的菱形
分成4个等腰三角形。
)72°
谢 谢
