华东师大版七年级下册数学 10.5 图形的全等 教案
文档属性
| 名称 | 华东师大版七年级下册数学 10.5 图形的全等 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 491.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 17:52:24 | ||
图片预览

文档简介
10.5 图形的全等
教学目标
【知识与技能】
1.借助具体情境和图案,经历观察、发现和实践操作重叠图形等过程.
2.了解图形全等的意义.
3.了解图形全等的特征.
【过程与方法】
学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣.
【情感态度】
学生积极参与图形全等的探究过程,从中体会合作与成功的快乐,建立学好数学的自信心,体会图形全等在现实生活中的应用价值.
【教学重点】
全等图形的意义及特征.
【教学难点】
识别全等图形.
教学过程
一回顾上节课你学到了什么?【教学说明】由复习中心对称定义和性质引出本节内容。学生口答第1个问题,第2题画图完成;
二情境导入,初步认识
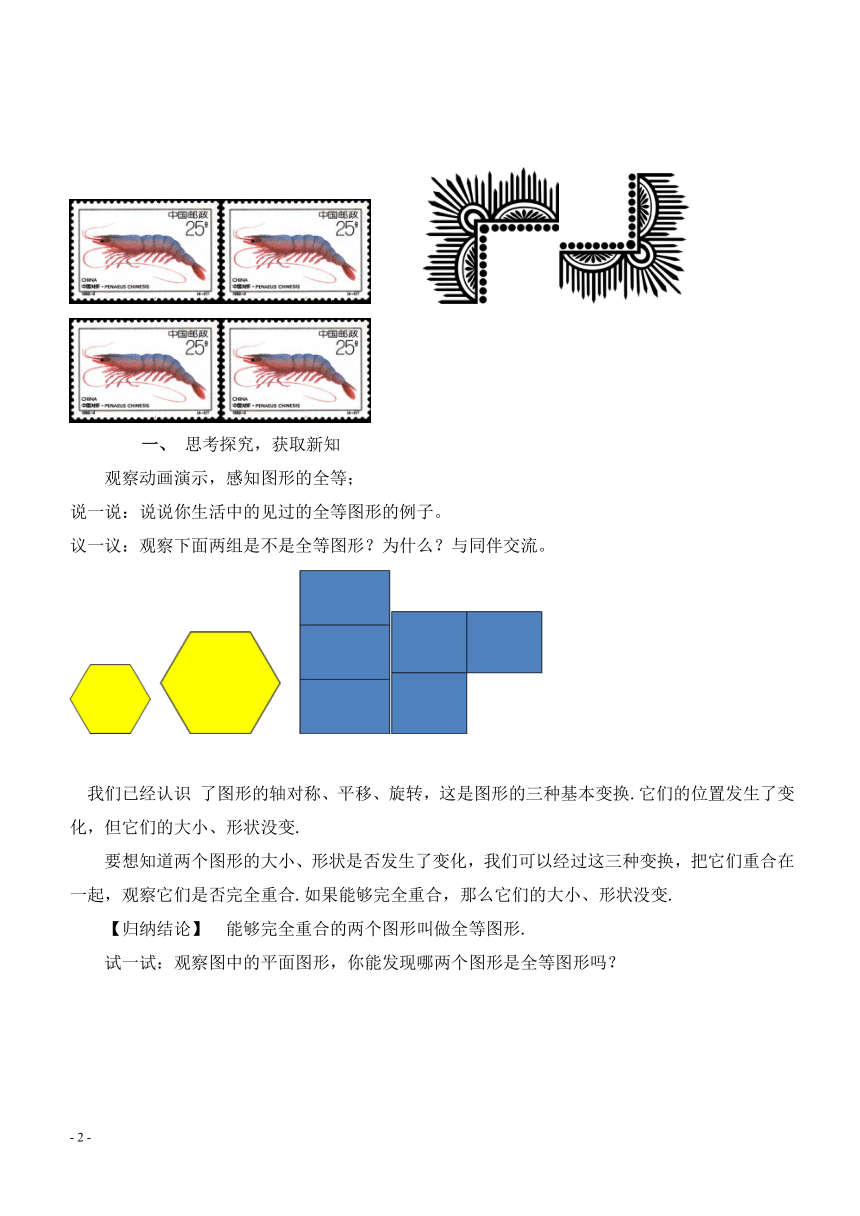
观察2组图片,他们有什么特点?
【教学说明】 学生观察图片,初步感知图形的全等.
- 2 -
- 3 -
思考探究,获取新知
观察动画演示,感知图形的全等;
说一说:说说你生活中的见过的全等图形的例子。
议一议:观察下面两组是不是全等图形?为什么?与同伴交流。
我们已经认识 了图形的轴对称、平移、旋转,这是图形的三种基本变换.它们的位置发生了变化,但它们的大小、形状没变.
要想知道两个图形的大小、形状是否发生了变化,我们可以经过这三种变换,把它们重合在一起,观察它们是否完全重合.如果能够完全重合,那么它们的大小、形状没变.
【归纳结论】 能够完全重合的两个图形叫做全等图形.
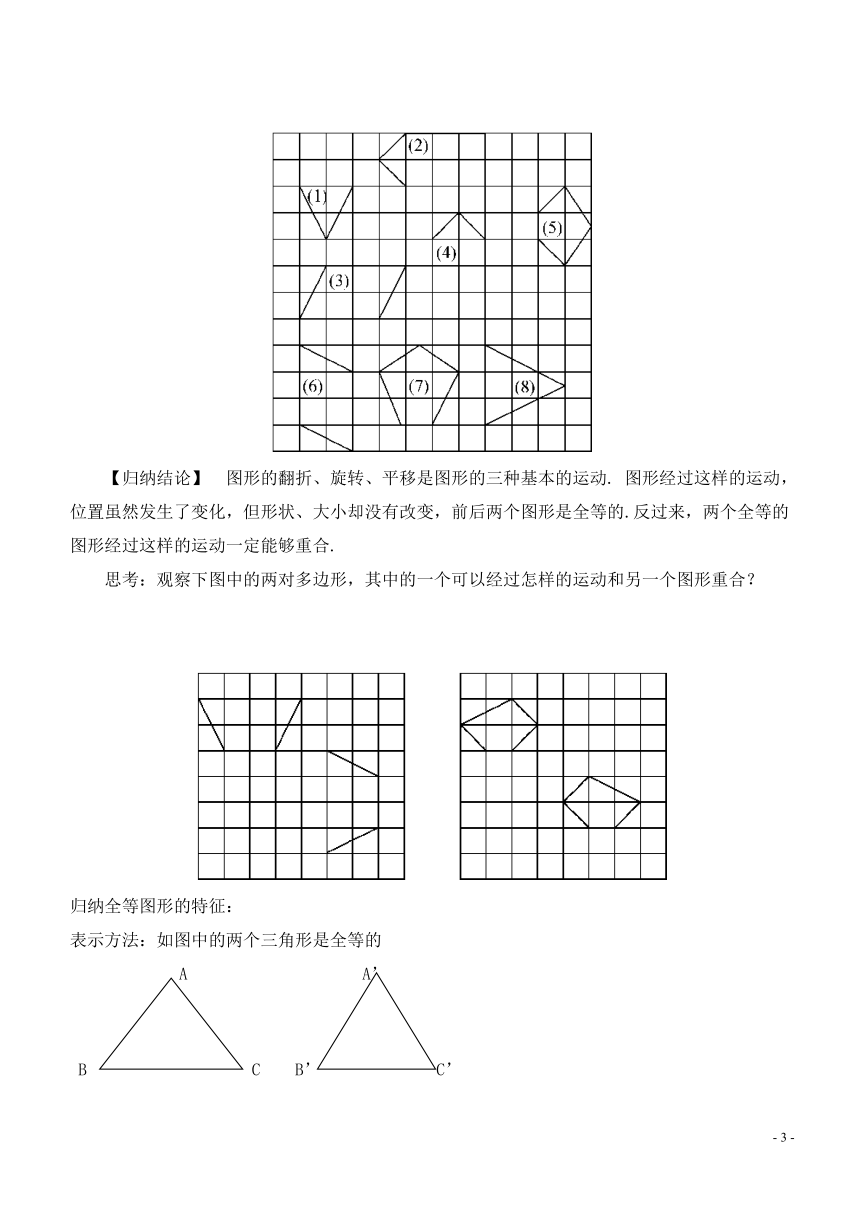
试一试:观察图中的平面图形,你能发现哪两个图形是全等图形吗?
【归纳结论】 图形的翻折、旋转、平移是图形的三种基本的运动. 图形经过这样的运动,位置虽然发生了变化,但形状、大小却没有改变,前后两个图形是全等的.反过来,两个全等的图形经过这样的运动一定能够重合.
思考:观察下图中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?
归纳全等图形的特征:
表示方法:如图中的两个三角形是全等的
A A’
B C B’ C’
记作: ABC ≌ A1B1C1
想一想:
A D
B C E F
能不能记做 ABC≌ DFE
上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过运动而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
如下图中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”.).点A与A′,B与B′,C与C′,D与D′,E与E′分别是对应顶点.
【归纳结论】 全等多边形的对应边、对应角分别相等.
这就是全等多边形的特征.实际上这也是我们识别全等多边形的方法,即边、角分别对应相等的两个多边形全等.
三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等.
同样,如果说一说:
全等多边形的性质
全等多边形的判定方法
全等三角形的性质
全等三角形的判定方法
两个三角形的边、角分别对应相等,那么这两个三角形全等.
如下图所示,△ABC≌△DEF.且 ∠A= ∠D ,∠B= ∠E 你能指出它们之间其他的对应顶点,对应角和对应边吗?
A D
C
E
B C F E
【教学说明】 通过探究,使学生了解全等图形、全等多边形、全等三角形的概念,掌握全等图形的性质.
想一想
1 如果 △ABC≌△DEF,那么你可以得到
2如果具备 AB=DE,BC=EF,AC=DF;
∠A= ∠D ,∠B= ∠E, ∠C= ∠F,那么可以得出
三、运用新知,深化理解
1.见教材第135页例题.
考考你:已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度。
A D
B C E F
如图,已知△ ABC和△ DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点
A D
B C
6.找出图中的全等图形:
【教学说明】 通过练习,检测学生掌握的情况,教师在作适当讲解.
四、师生互动,课堂小结
1 全等图形:
2 全等多形:
3. 对应顶点 对应边 对应角
4.全等多边形的性质:
5.全等多边形的判定方法:
6.全等三角形的性质:
7.全等三角形的判定方法:
1.布置作业:教材第136页“习题10.5”中第1、2、3题.
2.完成练习册中本课时练习.
教学反思
通过这节课的教学实践,使教师认识到.教学必须紧密联系学生的生活和实际,使学生对所学的内容兴趣盎然,乐于探究.教师最精彩的表现应该是高明的引导者、组织者、合作者,而不是舞台的主人——演员.全面的培养学生的创新意识与实践能力.
教学目标
【知识与技能】
1.借助具体情境和图案,经历观察、发现和实践操作重叠图形等过程.
2.了解图形全等的意义.
3.了解图形全等的特征.
【过程与方法】
学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣.
【情感态度】
学生积极参与图形全等的探究过程,从中体会合作与成功的快乐,建立学好数学的自信心,体会图形全等在现实生活中的应用价值.
【教学重点】
全等图形的意义及特征.
【教学难点】
识别全等图形.
教学过程
一回顾上节课你学到了什么?【教学说明】由复习中心对称定义和性质引出本节内容。学生口答第1个问题,第2题画图完成;
二情境导入,初步认识
观察2组图片,他们有什么特点?
【教学说明】 学生观察图片,初步感知图形的全等.
- 2 -
- 3 -
思考探究,获取新知
观察动画演示,感知图形的全等;
说一说:说说你生活中的见过的全等图形的例子。
议一议:观察下面两组是不是全等图形?为什么?与同伴交流。
我们已经认识 了图形的轴对称、平移、旋转,这是图形的三种基本变换.它们的位置发生了变化,但它们的大小、形状没变.
要想知道两个图形的大小、形状是否发生了变化,我们可以经过这三种变换,把它们重合在一起,观察它们是否完全重合.如果能够完全重合,那么它们的大小、形状没变.
【归纳结论】 能够完全重合的两个图形叫做全等图形.
试一试:观察图中的平面图形,你能发现哪两个图形是全等图形吗?
【归纳结论】 图形的翻折、旋转、平移是图形的三种基本的运动. 图形经过这样的运动,位置虽然发生了变化,但形状、大小却没有改变,前后两个图形是全等的.反过来,两个全等的图形经过这样的运动一定能够重合.
思考:观察下图中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?
归纳全等图形的特征:
表示方法:如图中的两个三角形是全等的
A A’
B C B’ C’
记作: ABC ≌ A1B1C1
想一想:
A D
B C E F
能不能记做 ABC≌ DFE
上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过运动而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
如下图中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”.).点A与A′,B与B′,C与C′,D与D′,E与E′分别是对应顶点.
【归纳结论】 全等多边形的对应边、对应角分别相等.
这就是全等多边形的特征.实际上这也是我们识别全等多边形的方法,即边、角分别对应相等的两个多边形全等.
三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等.
同样,如果说一说:
全等多边形的性质
全等多边形的判定方法
全等三角形的性质
全等三角形的判定方法
两个三角形的边、角分别对应相等,那么这两个三角形全等.
如下图所示,△ABC≌△DEF.且 ∠A= ∠D ,∠B= ∠E 你能指出它们之间其他的对应顶点,对应角和对应边吗?
A D
C
E
B C F E
【教学说明】 通过探究,使学生了解全等图形、全等多边形、全等三角形的概念,掌握全等图形的性质.
想一想
1 如果 △ABC≌△DEF,那么你可以得到
2如果具备 AB=DE,BC=EF,AC=DF;
∠A= ∠D ,∠B= ∠E, ∠C= ∠F,那么可以得出
三、运用新知,深化理解
1.见教材第135页例题.
考考你:已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度。
A D
B C E F
如图,已知△ ABC和△ DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点
A D
B C
6.找出图中的全等图形:
【教学说明】 通过练习,检测学生掌握的情况,教师在作适当讲解.
四、师生互动,课堂小结
1 全等图形:
2 全等多形:
3. 对应顶点 对应边 对应角
4.全等多边形的性质:
5.全等多边形的判定方法:
6.全等三角形的性质:
7.全等三角形的判定方法:
1.布置作业:教材第136页“习题10.5”中第1、2、3题.
2.完成练习册中本课时练习.
教学反思
通过这节课的教学实践,使教师认识到.教学必须紧密联系学生的生活和实际,使学生对所学的内容兴趣盎然,乐于探究.教师最精彩的表现应该是高明的引导者、组织者、合作者,而不是舞台的主人——演员.全面的培养学生的创新意识与实践能力.
