16.1 二次根式(第2课时)习题课件(含答案)
文档属性
| 名称 | 16.1 二次根式(第2课时)习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览





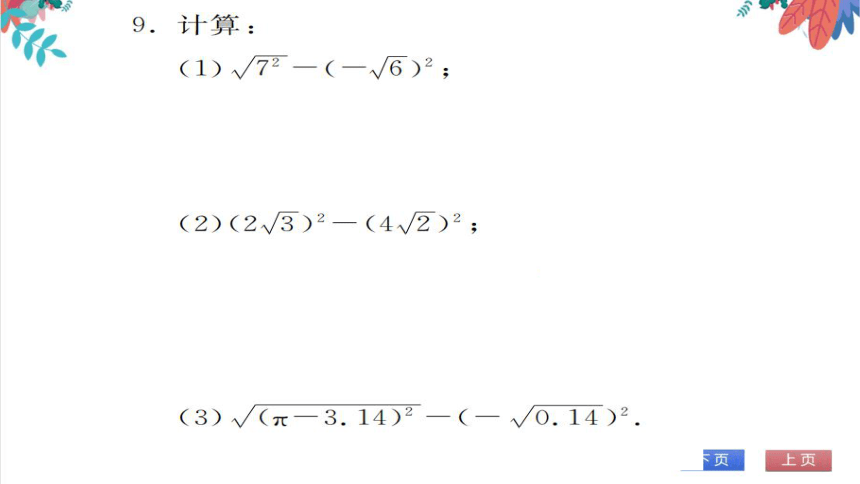
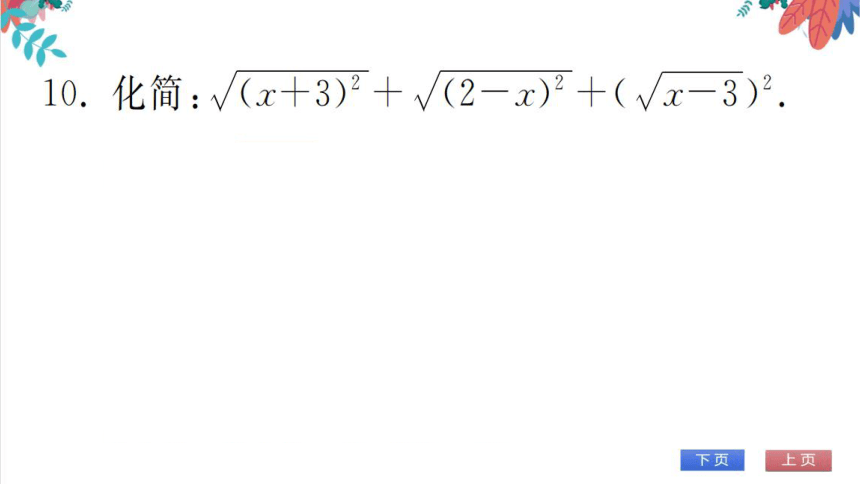
文档简介
(共15张PPT)
第2课时 二次根式(二)
下页
上页
课前预习
预习新矢
1.二次根式的性质
(1)(a)
(a≥0);
a(a≥0),
(2)
a(a<0).
2.用基本运算符号把数或表示数的字母
连接起来的式子称为代数式
当堂训练
巩固基础
知识点1二次根式的性质:a)2=a(a≥0)
计算(-7)2的结果是
B.
2.计算:
(1)(√3)
(2)(-2√2)
(3
6;(4)(√ab)
ab
2
3.等式(√x-4)2=x-4成立的条件是x≥4
知识点2二次根式的性质:(√a2)=a(a≥0)
4.(宜宾)二次根式√(-3)2的值是
B.3或-3
5.(浙江)下列计算正确的是
A.√22=2
B.√22=±2
D.√42=±2
若√(3-b)2=b-3,则
A.b>3B.b<3C.b≥3D.b≤3
计算:
4
4
(2)√(-5)
(3)√(3-2)
2-3
(4)√4×10
0.02
14
(5)2
2
8.(乐山)在数轴上表示实数a的点如图所示,化
简√(a-5)2+a-2的结果为3
计算
(1)√72-(-√6)2;
解:原式=7-6=1
(2)(2√3)2-(4√2)2;
解:原式=12-32=-20
(3)√(x-3.14)
0.14)
解:原式=x-3.14-0.14=x-3.28
0.化简:√(x+3)
(2-x)2+(√x-3)
解:由√x-3,得x-3≥0
x+3>0,2-x<0
原式=x+3+2-x+(x-3)=x+
3+
tx
知识点3代数式的定义
11.下列各式不是代数式的是
A
3x+5
C. (a+b
abb
2021
知识点4在实数范围内因式分解
12.在实数范围内分解因式:
(1)x2-5=(x+5)(x-√5);
(2)2x2-4=2(x+√2)(x-√2
课后作业
全面提升
1.(济宁)下列计算正确的是
B.
36
2.下列式子中属于代数式的有
(A
①0;②x;③x+2;④2x;⑤x=2;⑥x>2
1;⑧x≠2
A.5个B.6个C.7个D.8个
3.如果√(x=2)2=2-x,那么
( B
2B.x≤2C
2D.x≥2
已知
b2=3,且ab>0,则a+b的
值为
A.8
B.
化简√x2-6x+9(3-x)2的结果为
C B
A.2x-6
B.0
C.6-2x
(凉州)当-14
2
第2课时 二次根式(二)
下页
上页
课前预习
预习新矢
1.二次根式的性质
(1)(a)
(a≥0);
a(a≥0),
(2)
a(a<0).
2.用基本运算符号把数或表示数的字母
连接起来的式子称为代数式
当堂训练
巩固基础
知识点1二次根式的性质:a)2=a(a≥0)
计算(-7)2的结果是
B.
2.计算:
(1)(√3)
(2)(-2√2)
(3
6;(4)(√ab)
ab
2
3.等式(√x-4)2=x-4成立的条件是x≥4
知识点2二次根式的性质:(√a2)=a(a≥0)
4.(宜宾)二次根式√(-3)2的值是
B.3或-3
5.(浙江)下列计算正确的是
A.√22=2
B.√22=±2
D.√42=±2
若√(3-b)2=b-3,则
A.b>3B.b<3C.b≥3D.b≤3
计算:
4
4
(2)√(-5)
(3)√(3-2)
2-3
(4)√4×10
0.02
14
(5)2
2
8.(乐山)在数轴上表示实数a的点如图所示,化
简√(a-5)2+a-2的结果为3
计算
(1)√72-(-√6)2;
解:原式=7-6=1
(2)(2√3)2-(4√2)2;
解:原式=12-32=-20
(3)√(x-3.14)
0.14)
解:原式=x-3.14-0.14=x-3.28
0.化简:√(x+3)
(2-x)2+(√x-3)
解:由√x-3,得x-3≥0
x+3>0,2-x<0
原式=x+3+2-x+(x-3)=x+
3+
tx
知识点3代数式的定义
11.下列各式不是代数式的是
A
3x+5
C. (a+b
abb
2021
知识点4在实数范围内因式分解
12.在实数范围内分解因式:
(1)x2-5=(x+5)(x-√5);
(2)2x2-4=2(x+√2)(x-√2
课后作业
全面提升
1.(济宁)下列计算正确的是
B.
36
2.下列式子中属于代数式的有
(A
①0;②x;③x+2;④2x;⑤x=2;⑥x>2
1;⑧x≠2
A.5个B.6个C.7个D.8个
3.如果√(x=2)2=2-x,那么
( B
2B.x≤2C
2D.x≥2
已知
b2=3,且ab>0,则a+b的
值为
A.8
B.
化简√x2-6x+9(3-x)2的结果为
C B
A.2x-6
B.0
C.6-2x
(凉州)当-1
2
