17.1 勾股定理(第1课时)习题课件(含答案)
文档属性
| 名称 | 17.1 勾股定理(第1课时)习题课件(含答案) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览





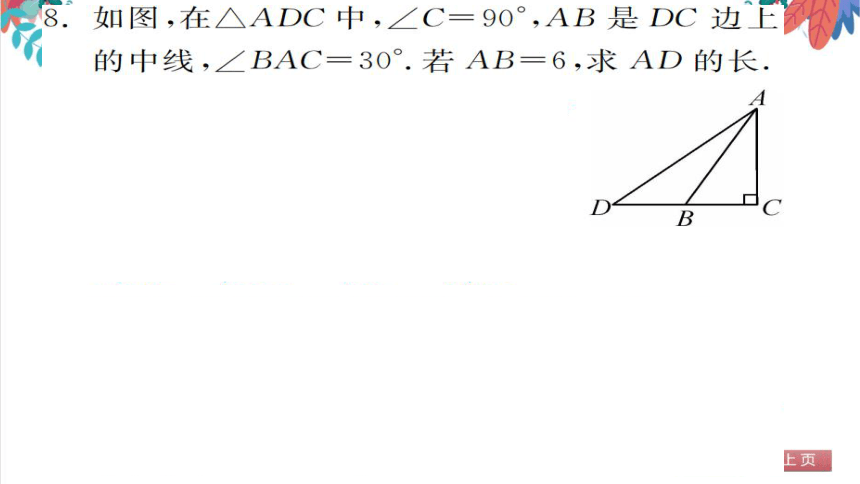
文档简介
(共14张PPT)
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理(一)
下页
上页
课前预习
习新知
1.如果直角三角形的两条直角边长分别为a,b,
斜边长为c,那么a2+b2=c2,直角三角形
的这种关系称为勾股定理,即在直角三角
形中两直角边的平方和等于斜边的平方
2.用数学语言表示为:
∴在△ABC中,
C=90
ACz+=AB
3.勾股定理的证明如“赵爽弦图”是
根据图形的面积关系得到数量关系,体现了
数形结合的思想方法
当堂训练
巩固基础
知识点1勾股定理的发现与证明
如图是美国总统 Garfield于1896年给出的
种验证勾股定理的方法,你能利用它证明勾股
定理吗 请写出证明过程
证明:根据面积法有
(b+a)(a+b)1
abt
a bb d
ab+c2,化简,得a2+b2=c2
知识点2勾股定理的运用
2.在Rt△ABC中,∠C=90°,a=12,b=16,则c
的长为
A.26
B.18
C.20
3.在Rt△ABC中,AB=3,AC=4,则BC的长为
B
5或7
D.不能确定
4.在△ABC中,∠A,∠B,∠C的对边分别为a,
b,c.若∠A+∠C=90°,则下列等式中成立
的是
A
B. b
c2=b2
b
若等腰三角形的腰长为10,底边长为12,则底
边上的高为
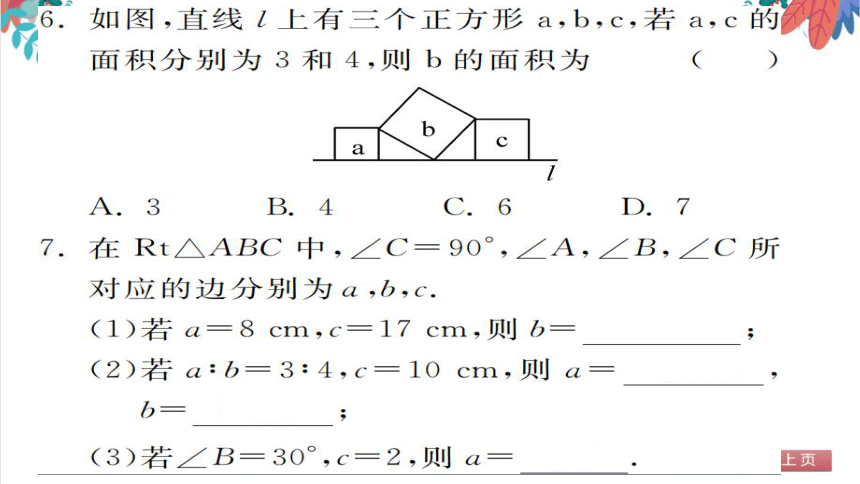
6.如图,直线l上有三个正方形a,b,c,若a,c的
面积分别为3和4,则b的面积为
7.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所
对应的边分别为a,b,c
(1)若a=8cm,c=17cm,则b=15cm;
(2)若a:b=3:4,c=10cm,则
cm
cm
(3)若∠B=30°,c=2,则a
图,在△ADC中,∠C=90°,AB是DC边上
的中线,∠BAC=30°.若AB=6,求AD的长
解:在Rt△ABC中,∠C=90°
BAC=30°,AB=6,
BC
AB=3,
D
B
∴AC=√AB2=BC=3√3
AB是DC边上的中线,DB=BC=3
CD=6
在Rt△ACD中,AD
AC2+CD2
课后作业
全面提升
1.下列说法中正确的是
A.已知a,b,c是直角三角形的三边长,则
B.在直角三角形中两直角边和的平方等于第
边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
2.如图,点P是平面直角坐标系中一点,则点P
到原点的距离是
A
A.3
B.√2
D.53
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理(一)
下页
上页
课前预习
习新知
1.如果直角三角形的两条直角边长分别为a,b,
斜边长为c,那么a2+b2=c2,直角三角形
的这种关系称为勾股定理,即在直角三角
形中两直角边的平方和等于斜边的平方
2.用数学语言表示为:
∴在△ABC中,
C=90
ACz+=AB
3.勾股定理的证明如“赵爽弦图”是
根据图形的面积关系得到数量关系,体现了
数形结合的思想方法
当堂训练
巩固基础
知识点1勾股定理的发现与证明
如图是美国总统 Garfield于1896年给出的
种验证勾股定理的方法,你能利用它证明勾股
定理吗 请写出证明过程
证明:根据面积法有
(b+a)(a+b)1
abt
a bb d
ab+c2,化简,得a2+b2=c2
知识点2勾股定理的运用
2.在Rt△ABC中,∠C=90°,a=12,b=16,则c
的长为
A.26
B.18
C.20
3.在Rt△ABC中,AB=3,AC=4,则BC的长为
B
5或7
D.不能确定
4.在△ABC中,∠A,∠B,∠C的对边分别为a,
b,c.若∠A+∠C=90°,则下列等式中成立
的是
A
B. b
c2=b2
b
若等腰三角形的腰长为10,底边长为12,则底
边上的高为
6.如图,直线l上有三个正方形a,b,c,若a,c的
面积分别为3和4,则b的面积为
7.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所
对应的边分别为a,b,c
(1)若a=8cm,c=17cm,则b=15cm;
(2)若a:b=3:4,c=10cm,则
cm
cm
(3)若∠B=30°,c=2,则a
图,在△ADC中,∠C=90°,AB是DC边上
的中线,∠BAC=30°.若AB=6,求AD的长
解:在Rt△ABC中,∠C=90°
BAC=30°,AB=6,
BC
AB=3,
D
B
∴AC=√AB2=BC=3√3
AB是DC边上的中线,DB=BC=3
CD=6
在Rt△ACD中,AD
AC2+CD2
课后作业
全面提升
1.下列说法中正确的是
A.已知a,b,c是直角三角形的三边长,则
B.在直角三角形中两直角边和的平方等于第
边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
2.如图,点P是平面直角坐标系中一点,则点P
到原点的距离是
A
A.3
B.√2
D.53
