17.1 勾股定理(第2课时)习题课件(含答案)
文档属性
| 名称 | 17.1 勾股定理(第2课时)习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览




文档简介
(共16张PPT)
第1课时 勾股定理(二)
下页
上页
课前预习
习新知
1.在将实际问题转化为数学问题时,关键是画出
符合题意的图形,把实际问题转化为几何问
题,直接利用直角三角形或构造直角三角形,
运用勾股定理求解
2.利用勾股定理可以在数轴上画出表示无理
数的点,说明实数与数轴上的点
对应
当堂训练
巩固基础
知识点1利用勾股定理建立方程模型解决实
际问题
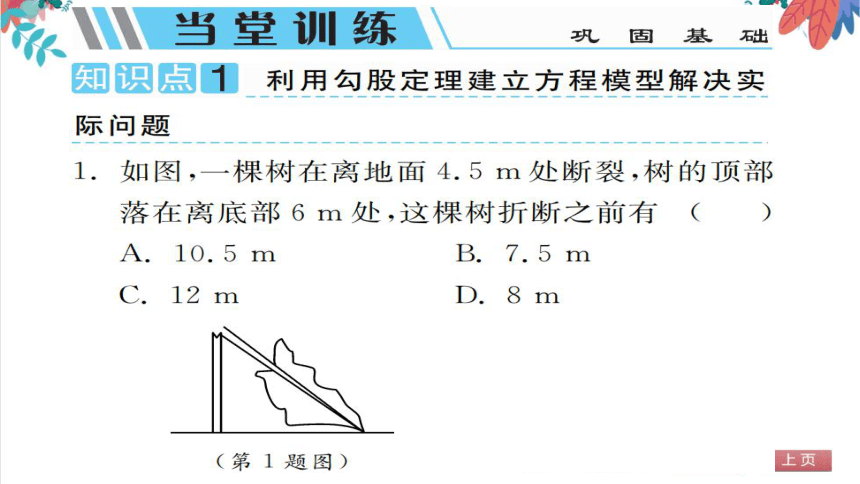
如图,一棵树在离地面4.5m处断裂,树的顶部
落在离底部6m处,这棵树折断之前有(C
A.10.5m
B.7.5m
m
(第1题图)
(第2题图
2.如图,小巷左右两侧是竖直的墙,一架梯子余
靠在左墙时,梯子底端到左墙角的距离为
0.7m,顶端距离地面2.4m,若保持梯子底端
位置不动,将梯子斜靠在右墙时,顶端距离地
面2m,则小巷的宽度为
A.0.7m
B
m
m
4
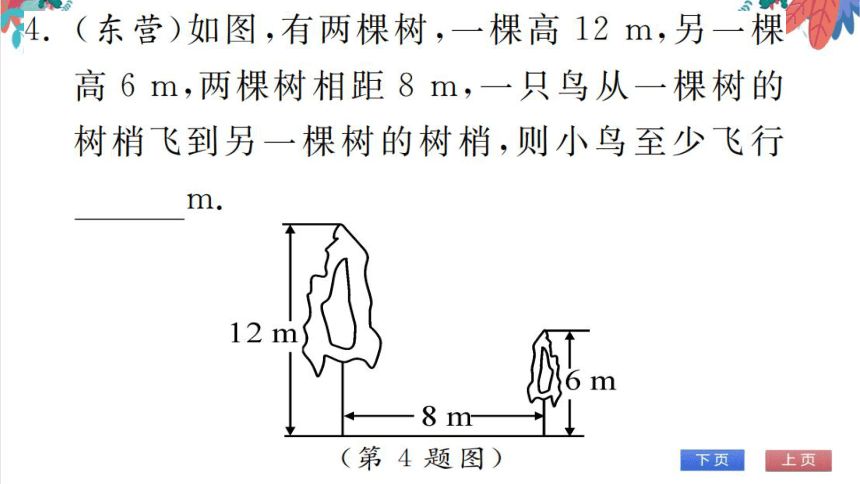
3.(河北)如图,从笔直的公路l旁一点P出发
向西走6km到达l;从P出发向北走6km也
到达l.下列说法错误的是
C A
A.从点P向北偏西45走3km到达l
B.公路L的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3km后,再向西走3km到
达l
义
十
12
6 m
第3题图)
(第4题图
(第4题图)
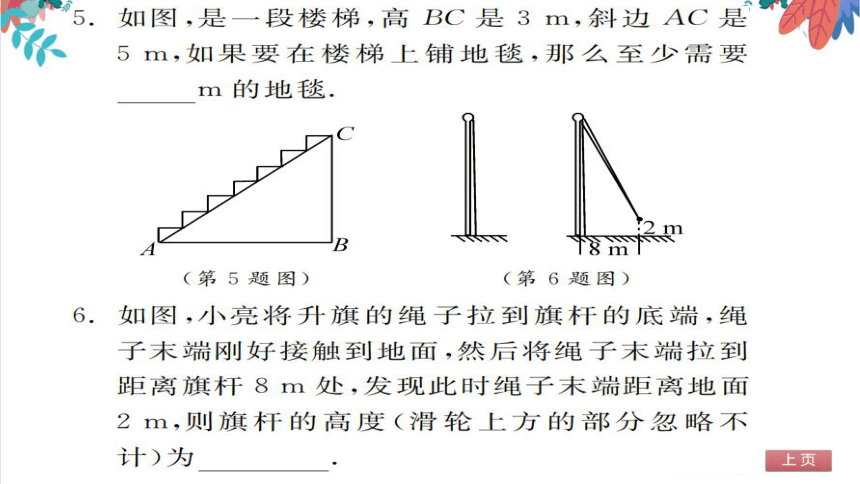
如图,是一段楼梯,高BC是3m,斜边AC是
m,如果要在楼梯上铺地毯,那么至少需要
7m的地毯
B
r8
(第5题图)
(第6题图)
6.如图,小亮将升旗的绳子拉到旗杆的底端,绳
子末端刚好接触到地面,然后将绳子末端拉到
距离旗杆8m处,发现此时绳子末端距离地面
2m,则旗杆的高度(滑轮上方的部分忽略不
计)为17m
7.现在人们锻炼身体的意识日渐增强,但是一些
人保护环境的意识却很淡薄.如图是某公园的
角,人为了抄近道而避开横平竖直的路的拐
角∠ABC,而走“捷径AC”,于是在草坪内走
出了一条不该有的“路AC”.已知AB=40m,
BC=30m,他们踩坏了50m的草坪,只为
少走20m的路.
(第7题图)
(第8题图)
知识点2在数轴上表示无理数
8.如图,在数轴上点A所表示的数为a,则a的
值为
(A
B.1
9.如图,点C表示的数是
B
D
1AC2
A.1
B.√2
课后作业
全面提升
如图,小明将一张长为20cm,宽为15cm的长
方形(AE>DE)剪去了一角,量得AB=3cm,
CD=4cm,则剪去的直角三角形的斜边长为
C D
A
cm
cm
cm
D. 20 cm
E
C D
(第1题图)
(第2题图
第1课时 勾股定理(二)
下页
上页
课前预习
习新知
1.在将实际问题转化为数学问题时,关键是画出
符合题意的图形,把实际问题转化为几何问
题,直接利用直角三角形或构造直角三角形,
运用勾股定理求解
2.利用勾股定理可以在数轴上画出表示无理
数的点,说明实数与数轴上的点
对应
当堂训练
巩固基础
知识点1利用勾股定理建立方程模型解决实
际问题
如图,一棵树在离地面4.5m处断裂,树的顶部
落在离底部6m处,这棵树折断之前有(C
A.10.5m
B.7.5m
m
(第1题图)
(第2题图
2.如图,小巷左右两侧是竖直的墙,一架梯子余
靠在左墙时,梯子底端到左墙角的距离为
0.7m,顶端距离地面2.4m,若保持梯子底端
位置不动,将梯子斜靠在右墙时,顶端距离地
面2m,则小巷的宽度为
A.0.7m
B
m
m
4
3.(河北)如图,从笔直的公路l旁一点P出发
向西走6km到达l;从P出发向北走6km也
到达l.下列说法错误的是
C A
A.从点P向北偏西45走3km到达l
B.公路L的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3km后,再向西走3km到
达l
义
十
12
6 m
第3题图)
(第4题图
(第4题图)
如图,是一段楼梯,高BC是3m,斜边AC是
m,如果要在楼梯上铺地毯,那么至少需要
7m的地毯
B
r8
(第5题图)
(第6题图)
6.如图,小亮将升旗的绳子拉到旗杆的底端,绳
子末端刚好接触到地面,然后将绳子末端拉到
距离旗杆8m处,发现此时绳子末端距离地面
2m,则旗杆的高度(滑轮上方的部分忽略不
计)为17m
7.现在人们锻炼身体的意识日渐增强,但是一些
人保护环境的意识却很淡薄.如图是某公园的
角,人为了抄近道而避开横平竖直的路的拐
角∠ABC,而走“捷径AC”,于是在草坪内走
出了一条不该有的“路AC”.已知AB=40m,
BC=30m,他们踩坏了50m的草坪,只为
少走20m的路.
(第7题图)
(第8题图)
知识点2在数轴上表示无理数
8.如图,在数轴上点A所表示的数为a,则a的
值为
(A
B.1
9.如图,点C表示的数是
B
D
1AC2
A.1
B.√2
课后作业
全面提升
如图,小明将一张长为20cm,宽为15cm的长
方形(AE>DE)剪去了一角,量得AB=3cm,
CD=4cm,则剪去的直角三角形的斜边长为
C D
A
cm
cm
cm
D. 20 cm
E
C D
(第1题图)
(第2题图
