17.2 勾股定理的逆定理(第2课时)习题课件(含答案)
文档属性
| 名称 | 17.2 勾股定理的逆定理(第2课时)习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览




文档简介
(共13张PPT)
第1课时 勾股定理的逆定理(二)
下页
上页
课前预习
预习新知
勾股定理的逆定理内容:若三角形的三边满
足两条边的平方和等于第三边的平方,那么这
个三角形是直角三角形
2.几何推理:在△ABC中,若AC+BC=AB
则CB=90°,也说△ABC是直角三角形
当堂训练
巩固基础
知织点1勾股定理逆定理的应用
1.在△ABC中,AC=BC=2,AB=2√2,则
△ABC中的最小角为
A.30
B.45
C.60
D.90
2.(长沙)我国南宋著名数学家秦九韶的著作《数
书九章》里记载有这样的一道题目:“问有沙田
块,有三斜,其中小斜五里,中斜十二里,大
斜十三里,欲知为田几何 ”这道题讲的是:有
块三角形沙田,三条边长分别为5里,12
里,13里,问这块沙田面积有多大 题中的
“里”是我国市制长度单位,1里=500m,则该
沙田的面积为
C A
A. 7.5 km
B. 15 km2
C. 75 km2
D.750km2
3.如图,学校B前面有一条笔直的
公路,学生放学后走BA,BC两
条路可到达公路,经测量BC
60m,BA=80m,AC=100m.现
需修建一条公路从学校B到公B
路,则学校B到公路的最短距离为48m
4.如图,甲、乙两船从港口A同时出发,甲船以
每小时30 n mile的速度向北偏东35°方向航
行,乙船以每小时40 n mile的速度向另一方
向航行,2h后,甲船到达C岛,乙船到达B
島,若C,B两岛相距100 n mile,则乙船航行
的角度是南偏东多少度
解:根据题意知∠EAC=35°,
C
AC=2×30=60( n mile),
AB=2×40=80( n mile
东
02+802=100
∴AC2+AB2=BC
F南
∴∠CAB=90
∴∠FAB=180-∠EAC-∠CAB=55°
故乙船航行的角度是南偏东
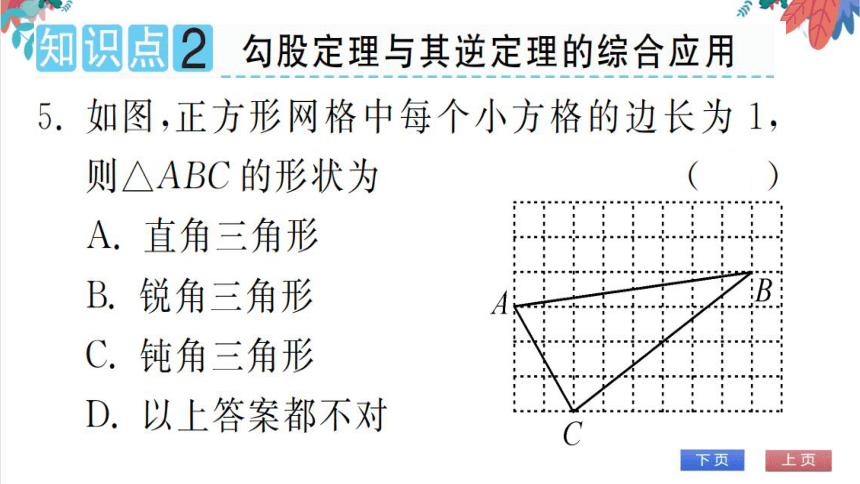
知识点2勾股定理与其逆定理的综合应用
5.如图,正方形网格中每个小方格的边长为1,
则△ABC的形状为
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
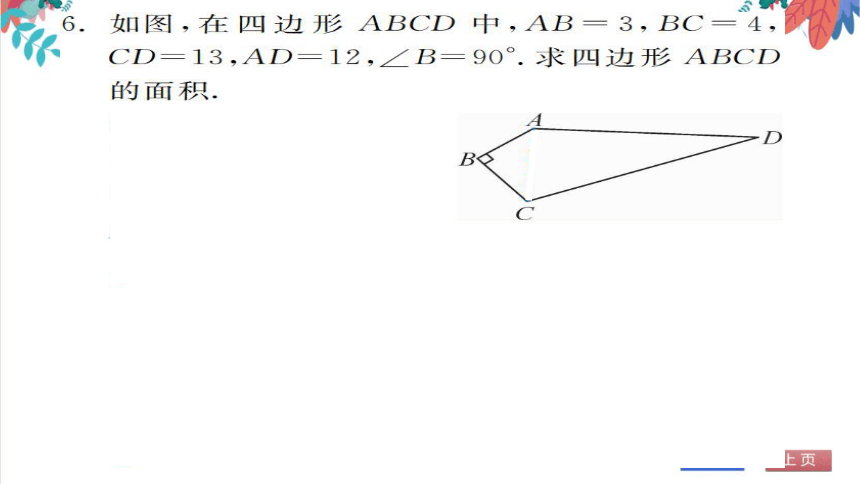
6.如图,在四边形ABCD中,AB=3,BC=4
CD=13,AD=12,∠B=90°.求四边形ABCD
的面积
解:连接AC
D
∠B=90°
B
∴由勾股定理,得
Ac
AB2+ BC2
32+42=5
AC2+AD2=25+144=169=CD2,
△ACD是直角三角形
∴S四边形ABCD=S△ABC+S△AC
×3×4+
×5×12=6+30=36
第1课时 勾股定理的逆定理(二)
下页
上页
课前预习
预习新知
勾股定理的逆定理内容:若三角形的三边满
足两条边的平方和等于第三边的平方,那么这
个三角形是直角三角形
2.几何推理:在△ABC中,若AC+BC=AB
则CB=90°,也说△ABC是直角三角形
当堂训练
巩固基础
知织点1勾股定理逆定理的应用
1.在△ABC中,AC=BC=2,AB=2√2,则
△ABC中的最小角为
A.30
B.45
C.60
D.90
2.(长沙)我国南宋著名数学家秦九韶的著作《数
书九章》里记载有这样的一道题目:“问有沙田
块,有三斜,其中小斜五里,中斜十二里,大
斜十三里,欲知为田几何 ”这道题讲的是:有
块三角形沙田,三条边长分别为5里,12
里,13里,问这块沙田面积有多大 题中的
“里”是我国市制长度单位,1里=500m,则该
沙田的面积为
C A
A. 7.5 km
B. 15 km2
C. 75 km2
D.750km2
3.如图,学校B前面有一条笔直的
公路,学生放学后走BA,BC两
条路可到达公路,经测量BC
60m,BA=80m,AC=100m.现
需修建一条公路从学校B到公B
路,则学校B到公路的最短距离为48m
4.如图,甲、乙两船从港口A同时出发,甲船以
每小时30 n mile的速度向北偏东35°方向航
行,乙船以每小时40 n mile的速度向另一方
向航行,2h后,甲船到达C岛,乙船到达B
島,若C,B两岛相距100 n mile,则乙船航行
的角度是南偏东多少度
解:根据题意知∠EAC=35°,
C
AC=2×30=60( n mile),
AB=2×40=80( n mile
东
02+802=100
∴AC2+AB2=BC
F南
∴∠CAB=90
∴∠FAB=180-∠EAC-∠CAB=55°
故乙船航行的角度是南偏东
知识点2勾股定理与其逆定理的综合应用
5.如图,正方形网格中每个小方格的边长为1,
则△ABC的形状为
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
6.如图,在四边形ABCD中,AB=3,BC=4
CD=13,AD=12,∠B=90°.求四边形ABCD
的面积
解:连接AC
D
∠B=90°
B
∴由勾股定理,得
Ac
AB2+ BC2
32+42=5
AC2+AD2=25+144=169=CD2,
△ACD是直角三角形
∴S四边形ABCD=S△ABC+S△AC
×3×4+
×5×12=6+30=36
