18.1.1 平行四边形的对角线的性质 习题课件(含答案)
文档属性
| 名称 | 18.1.1 平行四边形的对角线的性质 习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览




文档简介
(共17张PPT)
第十八章 平行四边形
18.1 平行四边形
18.1.1 平行四边形的性质
第2课时 平行四边形的对角线的性质
下页
上页
课前预习
习新知
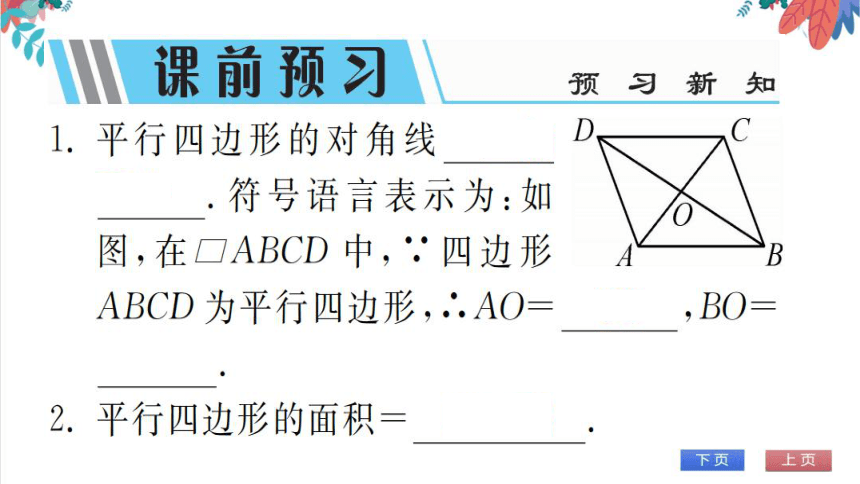
平行四边形的对角线互相
平分.符号语言表示为:如
图,在□ABCD中,四边形
ABCD为平行四边形,∴AO=CO,BO
2.平行四边形的面积=底×高
当堂训练
巩固基础
知识点1平行四边形的对角线互相平分的性
质及应用
如图,在□ABCD中,AC与BD相交于点O
则下列说法错误的是
A OB=OD
B.∠BAD=∠BCD
C/ BCD
CBA=180°
D. AO=DO
2.(丽水)如图,□ABCD的对角线AC,BD相交
于点O,已知AB=8,BD=12,AC=6,则
△DOC的周长为
( B
A.13
B.17
C.20
D.26
3.平行四边形的一边长为8,那么它的两条对角
线的长可能是
A.2和4
B.4和6
C.6和10
D.22和10
4.(临沂)如图,在□ABCD中,AB=10,AD=6,
AC⊥BC,则BD=413
B
(第4题图
5.(衡阳)如图,ABCD的对角线相交于点O,
且AD≠CD,过点O作OM⊥AC,交AD于点
M.如果△CDM的周长为8,那么□ABCD的
周长是16
6.(淮安)如图,□ABCD的对角线AC,BD相交
于点O,过点O的直线分别与AD,BC相交于
点E,F.求证:AE=CF
证明:∵□ABCD的对角
线AC,BD相交于点O
∴AO=CO,AD∥BC
B
∠EAO=∠FCO
∠EAO=∠FCO
在△AOE和△COF中,AO=CO
∠AOE=∠COF
△AOE≌△COF(ASA).∴AE=CF
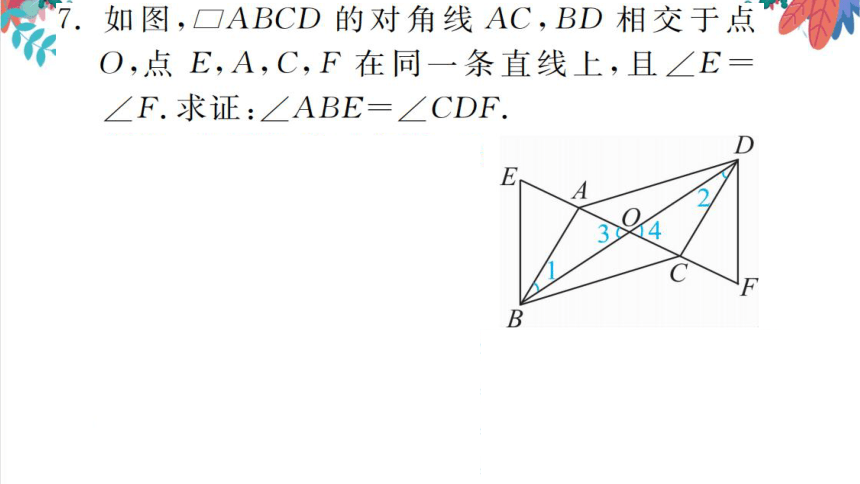
7.如图,□ABCD的对角线AC,BD相交于点
O,点E,A,C,F在同一条直线上,且∠E
F.求证:∠ABE=∠CDF
证明:∵四边形ABCD是
D
平行四边形,
AB∥CD,OB=OD
在△BOE和△DOF中
B
∠E=∠F
∠3=∠4,
OB=OD
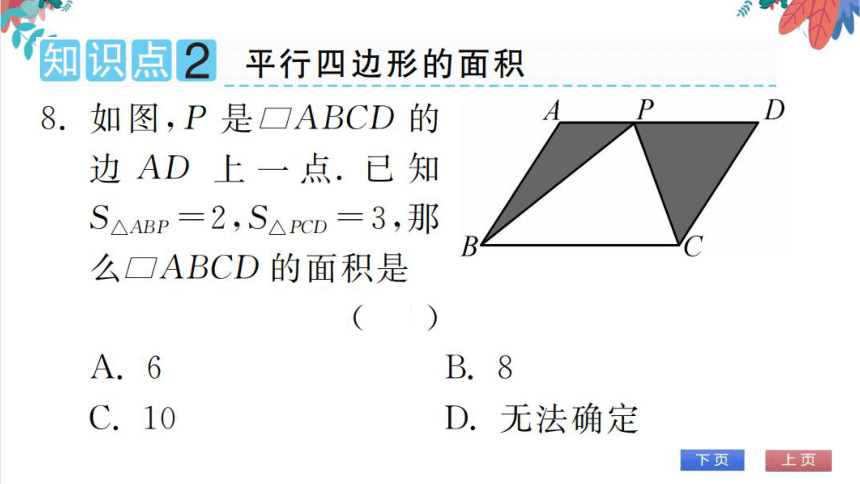
知识点2平行四边形的面积
8.如图,P是□ABCD的
边AD上一点.已知
S△ABP=2,S△PCD=3,那
B
么□ABCD的面积是
B.8
C.10
D.无法确定
9.如图,四边形ABCD是平行四边形,若
□ABCD
2,则S阴影
D
B4
B
(第9题图)
(第10题图)
10.如图,在□ABCD中,AD⊥BD,AB=4,
bd 3
ab 4
那么□ABCD的面积为
第十八章 平行四边形
18.1 平行四边形
18.1.1 平行四边形的性质
第2课时 平行四边形的对角线的性质
下页
上页
课前预习
习新知
平行四边形的对角线互相
平分.符号语言表示为:如
图,在□ABCD中,四边形
ABCD为平行四边形,∴AO=CO,BO
2.平行四边形的面积=底×高
当堂训练
巩固基础
知识点1平行四边形的对角线互相平分的性
质及应用
如图,在□ABCD中,AC与BD相交于点O
则下列说法错误的是
A OB=OD
B.∠BAD=∠BCD
C/ BCD
CBA=180°
D. AO=DO
2.(丽水)如图,□ABCD的对角线AC,BD相交
于点O,已知AB=8,BD=12,AC=6,则
△DOC的周长为
( B
A.13
B.17
C.20
D.26
3.平行四边形的一边长为8,那么它的两条对角
线的长可能是
A.2和4
B.4和6
C.6和10
D.22和10
4.(临沂)如图,在□ABCD中,AB=10,AD=6,
AC⊥BC,则BD=413
B
(第4题图
5.(衡阳)如图,ABCD的对角线相交于点O,
且AD≠CD,过点O作OM⊥AC,交AD于点
M.如果△CDM的周长为8,那么□ABCD的
周长是16
6.(淮安)如图,□ABCD的对角线AC,BD相交
于点O,过点O的直线分别与AD,BC相交于
点E,F.求证:AE=CF
证明:∵□ABCD的对角
线AC,BD相交于点O
∴AO=CO,AD∥BC
B
∠EAO=∠FCO
∠EAO=∠FCO
在△AOE和△COF中,AO=CO
∠AOE=∠COF
△AOE≌△COF(ASA).∴AE=CF
7.如图,□ABCD的对角线AC,BD相交于点
O,点E,A,C,F在同一条直线上,且∠E
F.求证:∠ABE=∠CDF
证明:∵四边形ABCD是
D
平行四边形,
AB∥CD,OB=OD
在△BOE和△DOF中
B
∠E=∠F
∠3=∠4,
OB=OD
知识点2平行四边形的面积
8.如图,P是□ABCD的
边AD上一点.已知
S△ABP=2,S△PCD=3,那
B
么□ABCD的面积是
B.8
C.10
D.无法确定
9.如图,四边形ABCD是平行四边形,若
□ABCD
2,则S阴影
D
B4
B
(第9题图)
(第10题图)
10.如图,在□ABCD中,AD⊥BD,AB=4,
bd 3
ab 4
那么□ABCD的面积为
