18.2.1 矩形的判定 习题课件(含答案)
文档属性
| 名称 | 18.2.1 矩形的判定 习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览





文档简介
(共18张PPT)
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形
第2课时 矩形的判定
下页
上页
课前预习
习新知
矩形的判定方法
(1)定义法:有个角是直角的平行四边形
是矩形;
(2)对角线相等的平行四边形是矩形
(3)有三个角是直角的四边形是矩形
当堂训练
巩固基础
知识点1有一个角是直角的平行四边形是矩形
1.下列说法正确的是
( D
A.有一组对角是直角的四边形一定是矩形
B.有一组邻角是直角的四边形一定是矩形
C.对角线互相平分的四边形是矩形
D.对角互补的平行四边形是矩形
如图,P是□ABCD的边AD4
的中点,且PB=PC,则四边
形ABCD是矩形,理由是
有一个角为直角的平行四边B
形是矩形
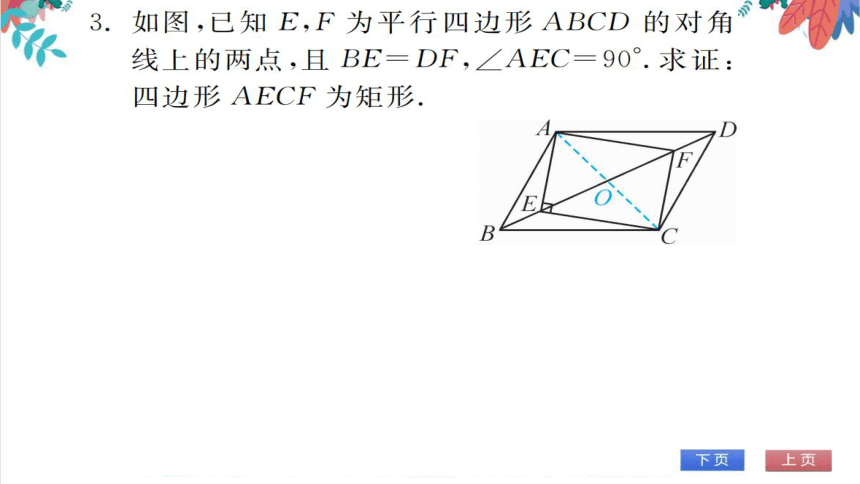
3.如图,知E,F为平行四边形ABCD的对角
线上的两点,且BE=DF,∠AEC=90°求证:
四边形AECF为矩形
证明:连接AC交BD于
点O
四边形ABCD是平
四边形,
B
OA=OC,OB=OD
BE=DE
OE=OF
又∵OA=OC,
四边形AECF是平行四边形
知识点2对角线相等的平行四边形是矩形
4.下列说法正确的是
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.对角线互相垂直且平分的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
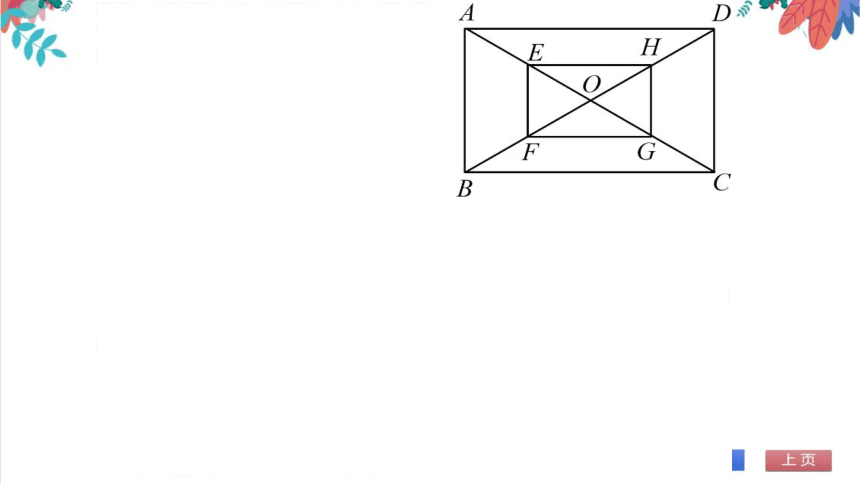
5.如图,矩形ABCD的对角线相交于点O,且E,
F,G,H分别是AO,BO,CO,DO的中点,请问
四边形EFGH是矩形吗 并说明理由
解:四边形EFGH是矩
D
形,理由如下
E
H
四边形ABCD是矩形
AC=BDOA=OC
AC,OB=0D≈1
BDB
∴AO=CO=DO=BO
又E,F,G,H分别是OA,OB,OC,OD的中
点,∴EO=OF=OG=OH
四边形EFGH是平行四边形
又∵EO+OG=FO+OH,即EG=FH
四边形EFGH是矩形
知识点3有三个角是直角的四边形是矩形
6.在数学活动课上,老师和同学们判断一个四边
形门框是否为矩形,下面是一个学习小组拟写
的方案,其中正确的是
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量其中三个角是否都为直角
证明::AB=AC,AD⊥BC,
∠CAD=∠BAC
N
AN平分∠MAC,
CAN
2CAD+∠CAN=1
∠BAC+∠CAM)
90°,即∠DAE=90°
AD⊥BC,CE⊥AN,
∴∠ADC=∠AEC=90
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形
第2课时 矩形的判定
下页
上页
课前预习
习新知
矩形的判定方法
(1)定义法:有个角是直角的平行四边形
是矩形;
(2)对角线相等的平行四边形是矩形
(3)有三个角是直角的四边形是矩形
当堂训练
巩固基础
知识点1有一个角是直角的平行四边形是矩形
1.下列说法正确的是
( D
A.有一组对角是直角的四边形一定是矩形
B.有一组邻角是直角的四边形一定是矩形
C.对角线互相平分的四边形是矩形
D.对角互补的平行四边形是矩形
如图,P是□ABCD的边AD4
的中点,且PB=PC,则四边
形ABCD是矩形,理由是
有一个角为直角的平行四边B
形是矩形
3.如图,知E,F为平行四边形ABCD的对角
线上的两点,且BE=DF,∠AEC=90°求证:
四边形AECF为矩形
证明:连接AC交BD于
点O
四边形ABCD是平
四边形,
B
OA=OC,OB=OD
BE=DE
OE=OF
又∵OA=OC,
四边形AECF是平行四边形
知识点2对角线相等的平行四边形是矩形
4.下列说法正确的是
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.对角线互相垂直且平分的四边形是矩形
D.对角线互相平分且相等的四边形是矩形
5.如图,矩形ABCD的对角线相交于点O,且E,
F,G,H分别是AO,BO,CO,DO的中点,请问
四边形EFGH是矩形吗 并说明理由
解:四边形EFGH是矩
D
形,理由如下
E
H
四边形ABCD是矩形
AC=BDOA=OC
AC,OB=0D≈1
BDB
∴AO=CO=DO=BO
又E,F,G,H分别是OA,OB,OC,OD的中
点,∴EO=OF=OG=OH
四边形EFGH是平行四边形
又∵EO+OG=FO+OH,即EG=FH
四边形EFGH是矩形
知识点3有三个角是直角的四边形是矩形
6.在数学活动课上,老师和同学们判断一个四边
形门框是否为矩形,下面是一个学习小组拟写
的方案,其中正确的是
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量其中三个角是否都为直角
证明::AB=AC,AD⊥BC,
∠CAD=∠BAC
N
AN平分∠MAC,
CAN
2
∠BAC+∠CAM)
90°,即∠DAE=90°
AD⊥BC,CE⊥AN,
∴∠ADC=∠AEC=90
