18.2.1 矩形的性质 习题课件(含答案)
文档属性
| 名称 | 18.2.1 矩形的性质 习题课件(含答案) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形
第1课时 矩形的性质
下页
上页
课前预习
须习新知
1.有一个角是直角的平行四边形叫做矩形,
矩形是特殊的平行四边形
2.矩形的性质:
(1)矩形的四个角都是直角
(2)矩形的对角线相等
3.直角三角形斜边上的中线等于斜边的一半
当堂训练
巩固基础
知识点1矩形的定义及性质
下列性质中,矩形具有但平行四边形不一定具
有的是
A.对边相等
B.对角相等
C.对角线相等
D.对边平行
2.如图,在矩形ABCD中,对角线AC,BD相交
于点O,∠AOB=60°,AB=2,则AC的长为
B
A.2
B.4
D.4√3
(吉林)如图,在矩形ABCD中,AB=5,AD
,矩形ABCD绕着点A逆时针旋转一定角
度,得到矩形ABCD,且B点对应点B′落在
DC上,则BC
4.(株洲)如图,矩形ABCD的对角线AC,BD相
交于点O,AC=10,P,Q分别为AO,AD的中
点,则PQ的长度为2.5
B
DYD
B
(第3题图)
A E
H
O
B F
(第5题图)
E
B
(第6题图)
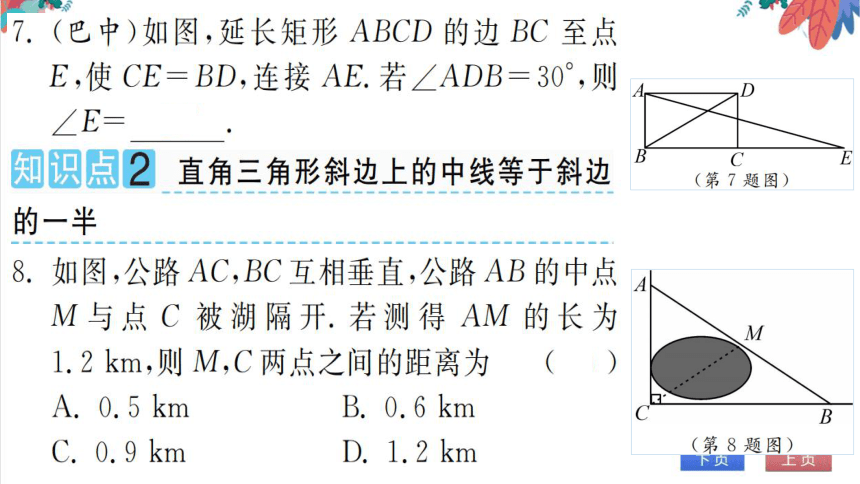
7.(巴中)如图,延长矩形ABCD的边BC至点
E,使CE=BD,连接AE.若∠ADB=30°,则
E
知识点2直角三角形斜边上的中线等于斜边
的一半
8.如图,公路AC,BC互相垂直,公路AB的中点
M与点C被湖隔开.若测得AM的长为
2km,则M,C两点之间的距离为(D
A. 0.5 km
B.0.6k:
c.o9 km
D.1.2k
M
B
(第8题图)
(徐州)如图,在Rt△ABC中,∠ABC=90°
D,E,F分别是AB,BC,AC的中点,若BF
5,则DE
0.直角三角形斜边上的高与中线分别是5cm
和6cm,则它的面积为30cm2
1.如图,BE,CF都是△ABC的高,M为BC的
中点,EF=4,BC=10.求△EFM的周长
解
BE,CF都是
△ABC的高,∴△BFC
△BEC都是直角三角形
E
点M为BC的中点,
BC=10
FM=EM-l
BC-5
∴△EFM的周长为EF+FM+EM=4+
5+5=14
课后作业
全面提升
1.(荆门)如图,在矩形ABCD中(AD>AB),E
是BC上一点,且DE=DA,AF⊥DE,垂足为
F,在下列结论中,不一定正确的是
(B)
A.△AFD≌△DCEB.AF
AD
C. AB=AF
D. BE=AD- DE
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形
第1课时 矩形的性质
下页
上页
课前预习
须习新知
1.有一个角是直角的平行四边形叫做矩形,
矩形是特殊的平行四边形
2.矩形的性质:
(1)矩形的四个角都是直角
(2)矩形的对角线相等
3.直角三角形斜边上的中线等于斜边的一半
当堂训练
巩固基础
知识点1矩形的定义及性质
下列性质中,矩形具有但平行四边形不一定具
有的是
A.对边相等
B.对角相等
C.对角线相等
D.对边平行
2.如图,在矩形ABCD中,对角线AC,BD相交
于点O,∠AOB=60°,AB=2,则AC的长为
B
A.2
B.4
D.4√3
(吉林)如图,在矩形ABCD中,AB=5,AD
,矩形ABCD绕着点A逆时针旋转一定角
度,得到矩形ABCD,且B点对应点B′落在
DC上,则BC
4.(株洲)如图,矩形ABCD的对角线AC,BD相
交于点O,AC=10,P,Q分别为AO,AD的中
点,则PQ的长度为2.5
B
DYD
B
(第3题图)
A E
H
O
B F
(第5题图)
E
B
(第6题图)
7.(巴中)如图,延长矩形ABCD的边BC至点
E,使CE=BD,连接AE.若∠ADB=30°,则
E
知识点2直角三角形斜边上的中线等于斜边
的一半
8.如图,公路AC,BC互相垂直,公路AB的中点
M与点C被湖隔开.若测得AM的长为
2km,则M,C两点之间的距离为(D
A. 0.5 km
B.0.6k:
c.o9 km
D.1.2k
M
B
(第8题图)
(徐州)如图,在Rt△ABC中,∠ABC=90°
D,E,F分别是AB,BC,AC的中点,若BF
5,则DE
0.直角三角形斜边上的高与中线分别是5cm
和6cm,则它的面积为30cm2
1.如图,BE,CF都是△ABC的高,M为BC的
中点,EF=4,BC=10.求△EFM的周长
解
BE,CF都是
△ABC的高,∴△BFC
△BEC都是直角三角形
E
点M为BC的中点,
BC=10
FM=EM-l
BC-5
∴△EFM的周长为EF+FM+EM=4+
5+5=14
课后作业
全面提升
1.(荆门)如图,在矩形ABCD中(AD>AB),E
是BC上一点,且DE=DA,AF⊥DE,垂足为
F,在下列结论中,不一定正确的是
(B)
A.△AFD≌△DCEB.AF
AD
C. AB=AF
D. BE=AD- DE
