18.2.2 菱形的判定 习题课件(含答案)
文档属性
| 名称 | 18.2.2 菱形的判定 习题课件(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 18:20:09 | ||
图片预览




文档简介
(共19张PPT)
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.2 菱形
第2课时 菱形的判定
下页
上页
课前预习
习新知
菱形的判定方法:
(1)定义法:有一组邻边相等的平行四边形
是菱形
(2)对角线互相垂直的平行四边形是菱形;
(3)四条边相等的四边形是菱形
当堂训练
巩固基础
知识点1有一组邻边相等的平行四边形是菱形
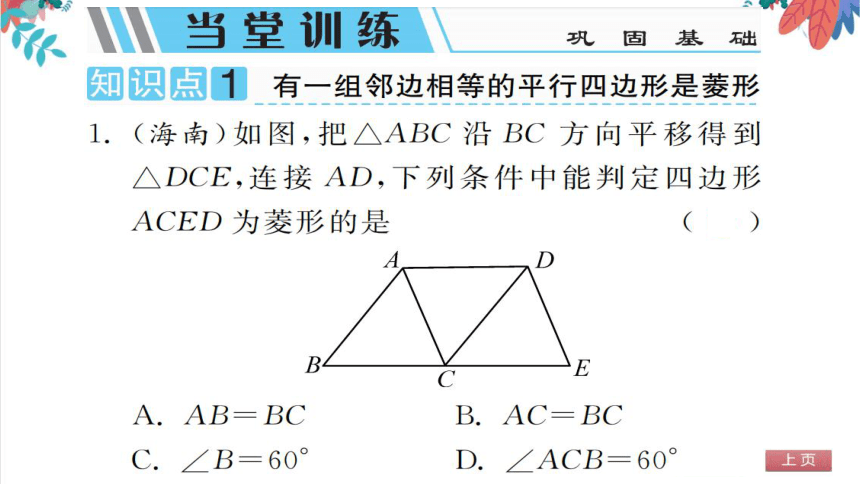
1.(海南)如图,把△ABC沿BC方向平移得到
△DCE,连接AD,下列条件中能判定四边形
ACED为菱形的是
B
D
B
E
A. AB=BC
B. AC=BC
C.∠B=60°
D.∠ACB=60°
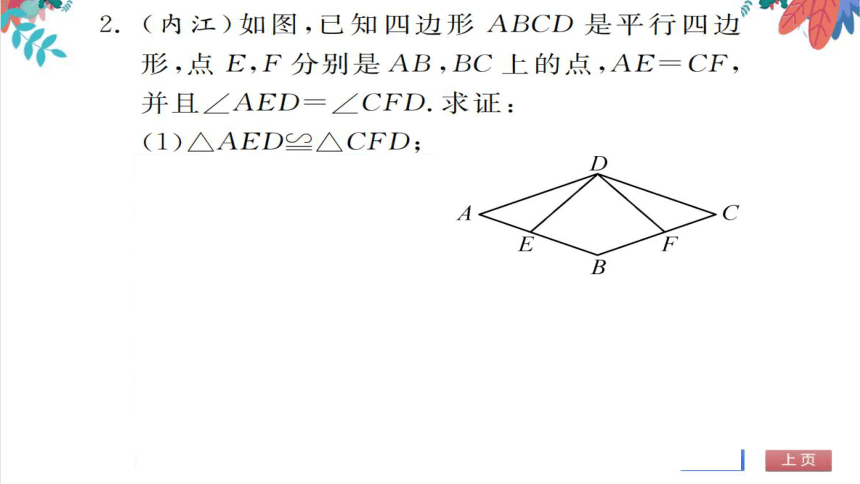
证明:(1)四边形
ABCD是平行四边形,A
C
∠A=∠
E
B
在△AED与△CFD中,
∠A=∠C
AE=CF
AED
CFD,
△AED≌△CFD(ASA)
知识点2对角线互相垂直的平行四边形是菱形
平行四边形的一条边长为9,两条对角线
的长分别是12和65,那么这个平行四边形
是菱形,理由:对角线互相垂直的平行
四边形是菱形
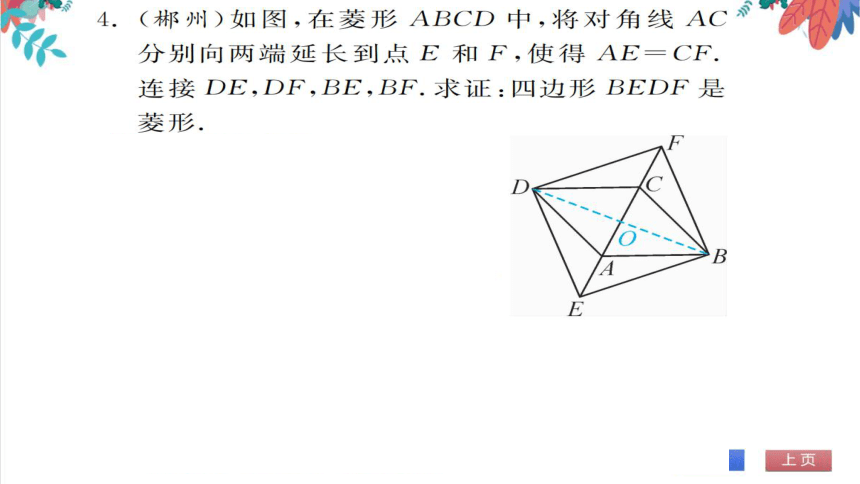
证明:连接BD
交AC于点O
D
四边形ABCD是菱形
∴OA=OC,OB=0D,AC
B
BD
E
AE=CF,∴,OE=OF
四边形BEDF是平行四边形
EF⊥BD
四边形BEDF是菱形
5.数学课上,老师让同学们判断一个四边形是否
为菱形,下面是某合作小组4位同学拟定的方
案,其中正确的是
A.测量对角线是否相等
B.测量对角线是否垂直
C.测量一组对角是否相等
D.测量四边是否相等
顶次连接矩形的四边中点得到的四边形是
菱形,顺次连接菱形的四边中点得到的四
边形是矩形
证明:由折叠的性质可得
△ABM≌△ADM
∴AB=AD,BM=DM,
∠AMB=∠AMD
B
∴DM∥AB
∴∠AMD=∠BAM
∠AMB=∠BAM
AB- BM
AB- BMEAD=DM
∴四边形ABMD是菱形
课后作业
全面提升
1.如图,在□ABCD中,对角线AC与BD相交
于点O.若增加一个条件,使□ABCD是菱形,
下列给出的条件不正确的是
A ab-aD
B.AC⊥BD
C. AC=BD
D.∠BAC=∠DAC
B
2.(舟山)用尺规在一个平行四边形内作菱形
ABCD,下列作法中错误的是
A
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.2 菱形
第2课时 菱形的判定
下页
上页
课前预习
习新知
菱形的判定方法:
(1)定义法:有一组邻边相等的平行四边形
是菱形
(2)对角线互相垂直的平行四边形是菱形;
(3)四条边相等的四边形是菱形
当堂训练
巩固基础
知识点1有一组邻边相等的平行四边形是菱形
1.(海南)如图,把△ABC沿BC方向平移得到
△DCE,连接AD,下列条件中能判定四边形
ACED为菱形的是
B
D
B
E
A. AB=BC
B. AC=BC
C.∠B=60°
D.∠ACB=60°
证明:(1)四边形
ABCD是平行四边形,A
C
∠A=∠
E
B
在△AED与△CFD中,
∠A=∠C
AE=CF
AED
CFD,
△AED≌△CFD(ASA)
知识点2对角线互相垂直的平行四边形是菱形
平行四边形的一条边长为9,两条对角线
的长分别是12和65,那么这个平行四边形
是菱形,理由:对角线互相垂直的平行
四边形是菱形
证明:连接BD
交AC于点O
D
四边形ABCD是菱形
∴OA=OC,OB=0D,AC
B
BD
E
AE=CF,∴,OE=OF
四边形BEDF是平行四边形
EF⊥BD
四边形BEDF是菱形
5.数学课上,老师让同学们判断一个四边形是否
为菱形,下面是某合作小组4位同学拟定的方
案,其中正确的是
A.测量对角线是否相等
B.测量对角线是否垂直
C.测量一组对角是否相等
D.测量四边是否相等
顶次连接矩形的四边中点得到的四边形是
菱形,顺次连接菱形的四边中点得到的四
边形是矩形
证明:由折叠的性质可得
△ABM≌△ADM
∴AB=AD,BM=DM,
∠AMB=∠AMD
B
∴DM∥AB
∴∠AMD=∠BAM
∠AMB=∠BAM
AB- BM
AB- BMEAD=DM
∴四边形ABMD是菱形
课后作业
全面提升
1.如图,在□ABCD中,对角线AC与BD相交
于点O.若增加一个条件,使□ABCD是菱形,
下列给出的条件不正确的是
A ab-aD
B.AC⊥BD
C. AC=BD
D.∠BAC=∠DAC
B
2.(舟山)用尺规在一个平行四边形内作菱形
ABCD,下列作法中错误的是
A
